The Black Model

Overview

In 1976 Fischer Black made some minor modifications to the Black Scholes model to adapt its use for evaluating options on futures contracts. The model takes into consideration the fact that there are no financing costs related to a futures contract. This results in a lower option price than for a similar option on equity that does not pay a dividend. The reason is as follows: If you were to replicate a call option using a portfolio of stock and a risk free bond, the Black Scholes model assumes that you finance the stock purchase at the risk free rate. The cost of this loan is embedded in the price of the option. Since the financing cost for a futures contract is zero, the option no longer has to include this premium.

The following assumptions apply to the Black model:

· the option can only be exercised on the expiry date (European style);

· the underlying instrument does not pay dividends;

· there are no taxes, margins or transaction costs;

· the risk free interest rate is constant;

· the price volatility of the underlying instrument is constant; and

· the price movements of the underlying instrument follow a lognormal distribution.

Formulas & Technical Details

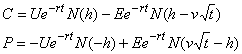
where:

is the theoretical value of a call

is the theoretical value of a put

is the price of the underlying futures contract

is the exercise price

is the time to expiration in years

is the annual volatility in percent

is the risk free interest rate

is the base of the natural logarithm

is the natural logarithm

is the cumulative normal density function

FINCAD Functions

aaBL (price_u, ex, d_exp, d_v, vlt, rate_ann, option_type, stat, acc)

Calculates fair value and risk statistics (delta, gamma, vega...) for European style options on futures using the Black '76 model

aaBL_iv (price_u, ex, d_exp, d_v, price, rate_ann, option_type, stat, acc)

Calculates implied volatility for European style options on futures using the Black '76 model

aaBL_sim (price_u, ex, d_exp, d_v, vlt, rate_ann, option_type, stat, acc, select_x, x_percent_orientation)

Simulates fair value and risk statistics (delta, gamma, vega...) for European style options on futures using the Black '76 model

aaBL_ED_fut (bpv, price_u, ex, d_exp, d_v, vlt, rate_dom, option_type, stat, acc)

Calculates fair value and risk statistics (delta, gamma, vega...) for European style options on eurodollar futures using the Black '76 model

aaBL_ik (price, price_u, d_exp, d_v, vlt, rate_ann, option_type, stat)

Calculates the implied strike price given the volatility and price of a European style call or put option using the black ’76 model

aaBL_iu (price, ex, d_exp, d_v, vlt, rate_ann, option_type, stat)

Calculates the implied underlying price given the volatility and price of a European style call or put option using the black ’76 model.

For details about the calculation of Greeks, see the Greeks of Options on non-Interest Rate Instruments FINCAD Math Reference document.

Example

You need to determine the fair value of a European style call option on a forward contract on fuel oil #2. The expiry date is June 1st, 1995 and the settlement date is March 1st, 1995. The futures price of fuel oil is $0.5550 per gallon and you want a strike of $0.5600. The three month Eurodollar rate is 6.05% (accrues on a 30/360 basis) and your research tells you that the 90 day historical volatility for fuel oil is about 29.5%.

aaBL

Argument	Description	Example Data	Switch
price_u	price of underlying interest	0.555
ex	exercise price	0.56
d_exp	expiry date	1-Jun-1995
d_v	settlement date	1-Mar-1995
vlt	annual volatility estimate	0.295
rate_ann	riskless deposit rate (annual compounding)	0.0605
option_type	option type	1	call
stat	statistics to be returned	1	fair value
acc	method of interest accrual	2	actual/ 360

Result

Statistic	Description	Value
1	Fair Value	0.030016

The fair value of the call option on the fuel oil #2 futures contract is $0.03 per gallon.

References

[1] Bookstaber, Richard, (1991), Option Pricing and Investment Strategies 3rd Edition, Probus Publishing Company.

[2] Cox, John; Rubinstein, Mark, (1985), Options Markets, Prentice Hall.

[3] ‘From Black Scholes to Black Holes’, (1994), Risk.

[4] Natenburg, Sheldon, (1988), Option Volatility and Pricing Strategies, Probus Publishing Company.

Disclaimer

With respect to this document, FinancialCAD Corporation (“FINCAD”) makes no warranty either express or implied, including, but not limited to, any implied warranty of merchantability or fitness for a particular purpose. In no event shall FINCAD be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of the use of this document or the information contained in it. This document should not be relied on as a substitute for your own independent research or the advice of your professional financial, accounting or other advisors.

This information is subject to change without notice. FINCAD assumes no responsibility for any errors in this document or their consequences and reserves the right to make changes to this document without notice.