Floating Rate Notes and Floating Legs of Swaps
Formulas & Technical Details
Calculating Interest Amounts
For the 
reset period (ISDA
“Compounding Period”), let:
be the
accrual factor from the effective date to the terminating date of the reset
period calculated using acc_reset
be
the accrual factor from the effective date to the terminating date of the reset
period calculated using acc_pay
be the spread over the reset rate
be the discount
factor from the accruing curve at the terminating date of the reset period
be the discount factor from the accruing curve at the effective
date of the reset period
be the reset rate (if already set) times scalefactor, or
else the scaled forward rate 
For a
particular coupon period (ISDA “Calculation Period”), let:
be the accrual factor from the effective date to the terminating
date of the coupon period calculated using acc_pay
be the spread over the compounded rate
be the notional principal amount
represent multiplication over resets periods
for this coupon period
be the number of
reset periods in this coupon period (e.g., 3 for quarterly pay/monthly reset)
Then for
“Straight Compounding”:
Interest amount = 
Equation 1
and
Compounded rate = 
Equation 2
where 
is the cumulative
interest amount for the compounding period,
and is defined recursively as:
Equation 3
.
Equation 4
The floating rate, augmented by the spread 
, is used to calculate the
interest amount for the current reset period (the first term), as well as to
compound the cumulative interest amount from previous reset periods (the second
term). This recursive equation has the
solution:
.
Equation 5
Note that 
in the normal case where acc_pay and acc_reset are
the same. In this case, and in the
absence of any spreads on the resets (i.e., 
), the formulae for
future periods reduce to:
Interest amount = 
,
Equation 6
and
Compounded rate = 
.
Equation 7
In this case,
the reset frequency does not affect the expected interest amount or the
compounded rate.
For “Flat Compounding”,
the recursive definition of 
becomes:
.
Equation 8
The
cumulative interest amount from previous reset periods is now compounded at the
flat floating rate (i.e., no spread added), although the interest amount for
the current reset period is still calculated using the augmented floating rate.
For “No Compounding”,
the recursive definition of 
becomes:
.
Equation 9
The
cumulative interest amount from previous reset periods is not compounded.
Calculating FRN Price
After the interest amounts have been determined, we can use
the discount factors from the discounting curve (df_crv_disc) to calculate the
present values of all the cash flows.
The sum of these present values is the FRN price.
However, if we are pricing the FRN using a discount margin
(as is done in the function aaFRN3_DM_p), we first modify the discounting
curve by adding the discount margin to the forward rates corresponding to the
reset periods.
To simplify the notation in this section, we will assume
that the reset frequency is the same as the payment frequency. We will also assume that the first date in
the discount factor curve (which we will call 
) is equal to a payment period effective date. Now, suppose there are 
cash flows remaining, then 
, where 
is the value date and 
(
) are the 
next cash flow dates.
Also, let:
be the accrual factor from 
to calculated using acc_reset
be the discount factor at
be the forward rate from 
to : 
be the discount margin
Then, the modified
discount factors are defined recursively by:
or explicitly by:
Now let 
be the discount factor
from the modified curve at the value date (which may need to be
interpolated). Then, if 
is the cash flow at , the FRN price (
) at the value date is given by:
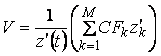
In the case where the accrual methods for the
reset and payment periods are the same (
), the reset frequency equals the payment frequency, the
discounting curve equals the accruing curve, and there is an exchange of
principal, we can write an explicit formula for the price in terms of the unmodified
discount factor values using the formula for coupons (Equation 6) from above:
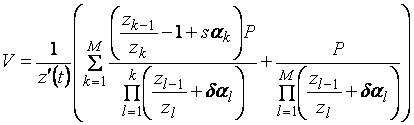
Using this formula with 
(i.e. the spread over
the reset rate is equal to the discount margin), it can be shown that the value
at 
is par, in other
words: 
.
Spread Duration
The functions aaFRN3_DM_p and aaFRN3_DM_sprd
both calculate spread duration, which is a measure of price sensitivity to
changes in the discount margin. If we use the notation from the previous
section, and define 
(one basis point),
then the spread duration is defined by:
Spread Duration = 
.
FINCAD Functions
Generated Dates, Non-Amortizing, Compounding
(Medium flexibility/Simple to use)
aaFRN, aaFRN2, aaFRN3:(d_v, d_e, d_t,
freq_pay_reset, position, cmpd_meth, npa, acc_pay, d_rul_pay, acc_rt,
d_rul_reset, reset_mktdays, reset_time, mgn_pay, mgn_reset, scale_factor,
asset, fixed_reset_tbl, intrp, dr_crv_acc, df_crv_disc, hl, stat)
Calculates the fair value, accrued interest and various
yields for an FRN or floating leg with regular interest payment (coupon)
periods and reset periods. The coupon
and reset frequencies may be any (allowable) combination of annual, semi-annual,
quarterly, monthly, biweekly, weekly and daily.
If the reset frequency is greater than the coupon frequency, then the
reset rates for each coupon are compounded.
The only difference between aaFRN2 and aaFRN is
that aaFRN2
has an additional switch which allows flat compounding to be selected (see
below for definition of flat compounding). aaFRN3 has an
additional input scalefactor, which is
applied to forward rates and reset rates before any spread is added; this
feature was added in order to handle “percentage of Libor” swaps more conveniently. aaFRN and aaFRN2
are retained for historical compatibility.
aaFRN_cf, aaFRN2_cf and aaFRN3_cf:(d_v,
d_e, d_t, freq_pay_reset, position, cmpd_meth, npa, acc_pay, d_rul_pay, acc_rt,
d_rul_reset, reset_mktdays, reset_time, mgn_pay, mgn_reset, scale_factor,
asset, fixed_reset_tbl, intrp, dr_crv_acc, df_crv_disc, hl, table type)
Calculates the expected future cash flows, present value
of future cash flows and implied rates for FRNs with regular coupon periods and
reset periods. aaFRN2_cf allows
flat compounding, while aaFRN_cf does not. aaFRN3_cf also handles “percentage of Libor” swaps via the scalefactor input.
aaFRN3_DM_p:(d_v,
d_e, d_t, freq_pay_reset, position, cmpd_meth, npa, acc_pay, d_rul_pay, acc_rt,
d_rul_reset, reset_mktdays, reset_time, mgn_pay, mgn_reset, scale_factor,
asset, fixed_reset_tbl, intrp, dr_crv_acc, df_crv_disc, discount_margin, hl,
stat)
Calculates the fair value given a discount margin for an
FRN or floating leg with regular interest payment (coupon) periods and reset
periods. Also calculates accrued
interest, various yields, and various risk statistics. The coupon and reset frequencies may be any
(allowable) combination of annual, semi-annual, quarterly, monthly, biweekly,
weekly and daily. If the reset frequency
is greater than the coupon frequency, then the reset rates for each coupon are
compounded.
aaFRN3_DM_sprd:(d_v,
d_e, d_t, dirty_price, freq_pay_reset, position, cmpd_meth, npa, acc_pay,
d_rul_pay, acc_rt, d_rul_reset, reset_mktdays, reset_time, mgn_pay, mgn_reset,
scale_factor, asset, fixed_reset_tbl, intrp, dr_crv_acc, df_crv_disc, hl, stat)
Calculates the implied discount margin given the value of
future cash flows (dirty price) for an FRN or floating leg with regular
interest payment (coupon) periods and reset periods. Also calculates accrued interest, various
yields, and various risk statistics. The
coupon and reset frequencies may be any (allowable) combination of annual,
semi-annual, quarterly, monthly, biweekly, weekly and daily. If the reset frequency is greater than the
coupon frequency, then the reset rates for each coupon are compounded.
Generated Dates, Amortizing, Compounding
(More flexibility/More inputs required)
aaFRN2_dgen, aaFRN2_dgen_cf:(d_v, d_e,
d_t, f, d_f_cpn, d_l_cpn, freq_pay_reset, frn_tbl_, position, cmpd_meth,
acc_pay, d_rul_pay, acc_rt, d_rul_reset, reset_mktdays, stub_method, mgn_pay,
mgn_reset, fixed_reset_tbl, intrp, dr_crv_acc, df_crv_disc, hl, stat, table
type)
Same as aaFRN2 and aaFRN2_cf (respectively) except that the
notional is allowed to vary, and principal payments can be specified on various
dates. These functions also take in
optional inputs specifying the dates of the first payment or the last payment
before maturity, thereby allowing odd first or last calculation periods,
whereas aaFRN2
and aaFRN2_cf do not
allow odd periods.
aaFRN3_dgen, aaFRN3_dgen_cf:(d_v,
d_e, d_t, f, d_f_cpn, d_l_cpn, freq_pay_reset, frn_tbl_, position, cmpd_meth,
acc_pay, d_rul_pay, acc_rt, d_rul_reset, reset_mktdays, stub_method, mgn_pay,
mgn_reset, scale_factor, fixed_reset_tbl, intrp, dr_crv_acc, df_crv_disc, hl,
stat, table type)
Same as aaFRN2_dgen, aaFRN2_dgen_cf with added scalefactor input.
Freestyle Dates, Amortizing, Compounding
(Maximum flexibility/Most inputs required)
aaFRN_fs, aaFRN2_fs:(d_v,
flleg_pay, flleg_r_rate, flleg_fixpay, dr_crv_acc, df_crv_disc, acc_rt,
acc_pay, intrp, position, cmpd_meth, stat)
Calculates the fair value, accrued interest and various
yields for an FRN or floating leg with user specified coupon dates, reset dates,
notional schedule and principal payments. aaFRN2_fs allows
flat compounding, while aaFRN_fs does not.
aaFRN_fs_cf, aaFRN2_fs_cf:(d_v,
flleg_pay, flleg_r_rate, flleg_fixpay, dr_crv_acc, df_crv_disc, acc_rt,
acc_pay, intrp, position, cmpd_meth, table_type)
Calculates the expected future cash flows, present value
of future cash flows and reset rates for an FRN or floating leg with user
specified coupon dates, reset dates, notional schedule and principal
payments. aaFRN2_fs_cf allows
flat compounding, while aaFRN_fs_cf does not.
aaFRN_fs_hist_cf:(pay_tb, reset_tb,
fixedpay_tb, acc_pay, position, method, table_type)
Calculates the historical cash flows (settlements) for an
FRN or floating leg with user specified coupon dates, reset dates, notional
schedule and principal payments.
Requires a full history of reset rates.
Allows flat compounding.
Generated Dates, Non-Amortizing, Non-Compounding
(Minimum flexibility/Simplest to use)
aaFloatlg_p:(d_v, d_e, d_m, d_f_cpn, d_l_cpn,
freq, position, npa, acc_pay, acc_reset, d_rul, mgn, asset, rate_reset, Intrp,
dr_crv_acc, df_crv_disc, hl, stat)
A simpler version of aaFRN in which the
coupon frequency and the reset frequency are the same, so there is no
compounding of resets. The rate is
assumed to be effective on the same day that it is set. Under these conditions there is at most one
active reset, so aaFloatlg_p takes in a single value for the
reset rate input, rather than a table of values as required by aaFRN. The function allows odd first or last
periods.
aaFloatlg_cf:(d_v, d_e, d_m, d_f_cpn, d_l_cpn,
freq, position, npa, acc_pay, acc_reset, d_rul, mgn, asset, rate_reset, Intrp,
dr_crv_acc, df_crv_disc, hl, table_type)
A simpler
version of aaFRN_cf
with no compounding, single reset rate input, and odd first/last
periods.
aaFloatlg2_p:(d_v, d_e, d_m, d_f_cpn, d_l_cpn,
freq, position, npa, acc_pay, acc_rt, d_rul, mgn, redemp_val, rate_reset,
Intrp, dr_crv_acc, df_crv_disc, hl, stat)
Same as aaFloatlg_p except that it allows for a
redemption price (per 100 notional), rather than a principal exchange switch.
aaFloatlg2_cf:(d_v, d_e, d_m, d_f_cpn, d_l_cpn,
freq, position, npa, acc_pay, acc_rt, d_rul, mgn, redemp_val, rate_reset,
Intrp, dr_crv_acc, df_crv_disc, hl, table_type)
Same as aaFloatlg_cf except that it allows for a
redemption price.
aaFloatlg3_p, aaFloatlg3_cf:( d_v, d_e, d_m, d_f_cpn, d_l_cpn,
freq, position, npa, acc_pay, acc_rt, d_rul, mgn, scale_factor, redemp_val,
rate_reset, Intrp, dr_crv_acc, df_crv_disc, hl, stat, table_type)
Same as aaFloatlg2* with added scalefactor input.
Date Generators
aaFRN_tables:(d_v,
d_t, d_e, freq_pay_reset, d_rul_pay, d_rul_reset, reset_mktdays, reset_time,
hl, table_type)
Calculates various dates related to these FRN deals. For instance, it calculates the dates for all
active resets. This is a utility
function which helps set up the input tables for calls to aaFRN,
aaFRN2, aaFRN_cf, aaFRN2_cf, and the freestyle (*_fs)
functions.
aaFRN_tables2:(d_s,
d_exp, d_e, d_f_cpn, d_l_cpn, freq_pay_reset, d_rul_pay, d_rul_reset,
reset_mkdays, reset_time, hl, table_type)
Similar to aaFRN_tables except
that aaFRN_tables2
also allows odd first or last periods. This function helps set up the input tables
for calls to aaFRN2_dgen
and aaFRN2_dgen_cf and the freestyle (*_fs)
functions.
Note:
Good examples of how to use the functions above are contained in the FINCAD
pre-built workbooks.
Description of Inputs
|
Input Argument |
Description |
|
d_v, d_e, d_t |
The value, effective
and terminating dates of the FRN or floating leg. In the case of Example #1, these are
30-Apr-2003, 1-Jan-2000 and 1-Jan-2010 respectively. |
|
Freq_pay_reset |
The frequencies of the
coupons and resets. In our example
this is 9 = semi-annual/monthly. |
|
Position |
1 = long, 2 = short |
|
npa |
Notional amount |
|
acc_pay |
The method used to
calculate the accrual factor for the interest payments. (e.g. act/365). |
|
acc_reset |
The method used to
calculate the accrual factor when extracting forward rates from the accruing
curve (e.g. act/365). The forward
rates are the expected values of the future reset rates. Usually acc_pay and acc_reset are the same. |
|
d_rul_pay, d_rul_reset |
The business day
convention of the coupons and the resets rates respectively. (e.g. next good
business day). |
|
reset_mktdays,
reset_time |
Setting reset_mktdays =
1, implies that the reset rates are set one market day prior to there
effective date. Reset_time specifies
the hour on this date, 12 = 12:00 noon.
(Setting reset_time = 0 may be sufficient for many purposes). |
|
asset |
1 = no exchange of
principal, 2 = exchange at the
effective and maturity dates, 3 = exchange of
principal at the maturity of the FRN. |
|
mgn_reset, mgn_pay |
Mgn_reset is a fixed margin (positive or negative) that
will be applied over each reset rate. Mgn_pay is a
margin that will be applied over the compounded rate. |
|
scalefactor |
Factor that is applied
to forward rates or reset rates prior to the addition of any margin. This is mainly for use in “percentage of
Libor” swaps – otherwise set to 1. |
|
fixed_reset_table |
A table containing the
active reset rate information. It may
be useful to use aaFRN_tables or aaFRN_tables2 to calculate the dates in this table. |
|
df_curve_acc |
A discount factor
curve for accruing. For example, if
the floating rate were calculated from LIBOR, this would be the LIBOR curve. |
|
df_curve_disc |
A discount factor
curve for discounting the cash flows.
For example, if the cash flows were to be paid by an AA counterparty
this would be the AA curve. |
|
hl |
A list of holidays. |
|
cmpd_meth |
Compounding
method. 1 = straight compounding, 2 = flat compounding, 3 = no compounding. |
|
discount_margin |
**This is only an
input for the function aaFRN3_DM_p, in which the price is calculated based on
this discount margin. It is the spread
which is added to the forward rates of the discounting curve. |
|
dirty_price |
**This input is only
used for the function aaFRN3_DM_sprd, in which the discount margin implied by this price is found. This is known in the output tables below as
“value of future cashflows (fair value +accrued)”. |
The freestyle functions have some special tables:
|
Input Argument |
Description |
|
Flleg_pay |
A table describing the
interest payment dates. Note that the
first input is an ID number. |
|
Flleg_r_rate |
A table describing the
reset rate dates. Note that the first
input of each reset rate row is an ID number, which must correspond to one of
the payment leg IDs. |
|
Flleg_fixpay |
A table of fixed
payment dates. For example, exchanges
of principal. |
Description of Outputs
Pricing functions
aaFRN, aaFRN2, aaFRN3, aaFRN2_dgen, aaFRN3_dgen, aaFRN_fs,
aaFRN2_fs, aaFloatlg_p, aaFloatlg2_p and aaFloatlg3_p
|
Output Statistic |
Description |
|
1 |
fair value |
|
2 |
accrued interest |
|
3 |
value of future cashflows (fair value +accrued) |
|
4 |
annually compounded yield |
|
5 |
semi-annually compounded yield |
|
6 |
quarterly compounded yield |
|
7 |
monthly compounded yield |
|
8 |
money market (actual/365) yield |
|
9 |
money market (actual/360) yield |
|
10 |
next cashflow date |
|
11 |
previous cashflow date |
|
12 |
number of days from value date to maturity |
|
13 |
years to maturity |
|
14 |
number of days from value date to next cashflow |
|
15 |
number of days of accrued interest |
|
16 |
number of remaining cashflows |
|
17 |
basis point value |
|
18 |
modified duration |
|
19 |
convexity |
|
20 |
current coupon |
|
21 |
current reset |
|
22 |
current notional |
These functions
output several statistics:
|
pricing statistics: |
fair value, accrued
interest, and fair value + accrued interest, |
|
yield to maturity
statistics: |
annually compounded,
semi-annually compounded, … |
Cash flow functions
aaFRN_cf, aaFRN2_cf, aaFRN3_cf, aaFRN2_dgen_cf,
aaFRN3_dgen_cf, aaFRN_fs_cf, aaFRN2_fs_cf, aaFloatlg_cf, aaFloatlg2_cf, and
aaFloatlg3_cf
|
Output Table Type |
Description |
|
Coupon Tables |
contains all
information related to the coupons, (e.g. coupon rates, cash flow, …) |
|
Reset tables |
contains all
information related to the reset rates |
|
Cash flow tables: |
contains all future
cash flow information (interest flows, principal flows and the present value
of each). |
Discount margin functions
aaFRN3_DM_p
|
Output Statistic |
Description |
|
1 |
fair value |
|
2 |
accrued interest |
|
3 |
value of future cash flows ( fair value + accrued) |
|
4 |
annually compounded yield |
|
5 |
semi-annually compounded yield |
|
6 |
quarterly compounded yield |
|
7 |
monthly compounded yield |
|
8 |
money market (actual/ 365) yield |
|
9 |
money market (actual/ 360) yield |
|
10 |
next cash flow date |
|
11 |
previous cash flow date |
|
12 |
number of days from value date to maturity |
|
13 |
years to maturity |
|
14 |
number of days from value date to next cash flow |
|
15 |
number of days of accrued interest |
|
16 |
number of remaining cash flows |
|
17 |
basis point value |
|
18 |
modified duration |
|
19 |
convexity |
|
20 |
current coupon |
|
21 |
current reset |
|
22 |
current notional |
|
23 |
spread duration (of discount margin) |
aaFRN3_DM_sprd
|
Output Statistic |
Description |
|
1 |
fair value |
|
2 |
accrued interest |
|
3 |
implied discount margin |
|
4 |
annually compounded yield |
|
5 |
semi-annually compounded yield |
|
6 |
quarterly compounded yield |
|
7 |
monthly compounded yield |
|
8 |
money market (actual/ 365) yield |
|
9 |
money market (actual/ 360) yield |
|
10 |
next cash flow date |
|
11 |
previous cash flow date |
|
12 |
number of days from value date to maturity |
|
13 |
years to maturity |
|
14 |
number of days from value date to next cash flow |
|
15 |
number of days of accrued interest |
|
16 |
number of remaining cash flows |
|
17 |
basis point value |
|
18 |
modified duration |
|
19 |
convexity |
|
20 |
current coupon |
|
21 |
current reset |
|
22 |
current notional |
|
23 |
spread duration (of discount margin) |
Examples
Example 1
Suppose the value date is 30-April-2003. Suppose we are valuing an FRN that was issued
(and started accruing interest) on
Step 1
Calculate the required reset dates using the function aaFRN_tables.
Setting table_type = 3 (active resets), the output is the first 4
columns of the following table:
|
ID |
reset date |
effective date |
terminating date |
rate |
|
1 |
Tue 31-Dec-2002 |
Thu 2-Jan-2003 |
Mon 3-Feb-2003 |
5.234% |
|
1 |
Fri 31-Jan-2003 |
Mon 3-Feb-2003 |
Mon 3-Mar-2003 |
5.345% |
|
1 |
Fri 28-Feb-2003 |
Mon 3-Mar-2003 |
Tue 1-Apr-2003 |
5.456% |
|
1 |
Mon 31-Mar-2003 |
Tue 1-Apr-2003 |
Thu 1-May-2003 |
5.567% |
|
1 |
Wed 30-Apr-2003 |
Thu 1-May-2003 |
Mon 2-Jun-2003 |
5.678% |
Active resets are those that affect the amount of
the next interest payment, and whose reset date is on or before the value
date. There are 5 rates that are
available on 30-April-2003. The 6th
rate, that will affect the payment on 1-July-2003, is not available until
30-May-2003. The rates must be supplied
in the fifth column. The complete table,
including the fifth column, serves as the reset table input to aaFRN and
aaFRN_cf.
This example illustrates the rule that applies when the
value date falls on a reset date (i.e., 30-April-03 here). In this case, if a positive rate is supplied
in the fifth column on the appropriate row, then it will be used. If the cell is left blank, or contains a zero
value, then a rate will be implied from the accruing curve.
Step 2
Calculate the main functions aaFRN2 and/or aaFRN2_cf. The output
from aaFRN2_cf is as
follows:
Table type #1: Cashflow Table
|
Date |
Interest Amount |
Principal Payment |
Total Payment |
PV Interest Amount |
PV Principal Payment |
PV Total Payment |
Accrued Interest |
|
Tue 1-Jul-2003 |
27,655 |
- |
27,655 |
27,427 |
- |
27,427 |
18,301 |
|
Fri 2-Jan-2004 |
25,728 |
- |
25,728 |
24,894 |
- |
24,894 |
- |
|
Thu 1-Jul-2004 |
25,196 |
- |
25,196 |
23,798 |
- |
23,798 |
- |
|
Mon 3-Jan-2005 |
25,938 |
- |
25,938 |
23,898 |
- |
23,898 |
- |
|
Fri 1-Jul-2005 |
24,962 |
- |
24,962 |
22,455 |
- |
22,455 |
- |
|
Tue 3-Jan-2006 |
25,938 |
- |
25,938 |
22,760 |
- |
22,760 |
- |
|
Mon 3-Jul-2006 |
25,245 |
- |
25,245 |
21,622 |
- |
21,622 |
- |
|
Tue 2-Jan-2007 |
25,515 |
- |
25,515 |
21,325 |
- |
21,325 |
- |
|
Mon 2-Jul-2007 |
25,221 |
- |
25,221 |
20,576 |
- |
20,576 |
- |
|
Wed 2-Jan-2008 |
25,587 |
- |
25,587 |
20,369 |
- |
20,369 |
- |
|
Tue 1-Jul-2008 |
25,196 |
- |
25,196 |
19,579 |
- |
19,579 |
- |
|
Fri 2-Jan-2009 |
25,797 |
- |
25,797 |
19,556 |
- |
19,556 |
- |
|
Wed 1-Jul-2009 |
25,104 |
- |
25,104 |
18,578 |
- |
18,578 |
- |
|
Mon 4-Jan-2010 |
26,080 |
1,000,000 |
1,026,080 |
18,824 |
721,787 |
740,611 |
- |
Each row represents a
cashflow, whether it be an interest payment, a principal payment, or both.
Table type #2: Reset Table
|
ID |
Reset Date |
Effective Date |
Terminating Date |
Reset/Forward Rate |
Rate + 5bp |
|
1 |
Tue 31-Dec-2002 |
Thu 2-Jan-2003 |
Mon 3-Feb-2003 |
5.234% |
5.284% |
|
1 |
Fri 31-Jan-2003 |
Mon 3-Feb-2003 |
Mon 3-Mar-2003 |
5.345% |
5.395% |
|
1 |
Fri 28-Feb-2003 |
Mon 3-Mar-2003 |
Tue 1-Apr-2003 |
5.456% |
5.506% |
|
1 |
Mon 31-Mar-2003 |
Tue 1-Apr-2003 |
Thu 1-May-2003 |
5.567% |
5.617% |
|
1 |
Wed 30-Apr-2003 |
Thu 1-May-2003 |
Mon 2-Jun-2003 |
5.678% |
5.728% |
|
1 |
Fri 30-May-2003 |
Mon 2-Jun-2003 |
Tue 1-Jul-2003 |
4.808% |
4.858% |
|
2 |
Mon 30-Jun-2003 |
Tue 1-Jul-2003 |
Fri 1-Aug-2003 |
4.969% |
5.019% |
|
2 |
Thu 31-Jul-2003 |
Fri 1-Aug-2003 |
Tue 2-Sep-2003 |
4.964% |
5.014% |
|
… |
etc… |
etc… |
etc… |
etc… |
etc… |
|
13 |
Thu 30-Apr-2009 |
Fri 1-May-2009 |
Mon 1-Jun-2009 |
4.983% |
5.033% |
|
13 |
Fri 29-May-2009 |
Mon 1-Jun-2009 |
Wed 1-Jul-2009 |
4.822% |
4.872% |
|
14 |
Tue 30-Jun-2009 |
Wed 1-Jul-2009 |
Mon 3-Aug-2009 |
4.974% |
5.024% |
|
14 |
Fri 31-Jul-2009 |
Mon 3-Aug-2009 |
Tue 1-Sep-2009 |
4.994% |
5.044% |
|
14 |
Mon 31-Aug-2009 |
Tue 1-Sep-2009 |
Thu 1-Oct-2009 |
4.822% |
4.872% |
|
14 |
Wed 30-Sep-2009 |
Thu 1-Oct-2009 |
Mon 2-Nov-2009 |
4.978% |
5.028% |
|
14 |
Fri 30-Oct-2009 |
Mon 2-Nov-2009 |
Tue 1-Dec-2009 |
4.822% |
4.872% |
|
14 |
Mon 30-Nov-2009 |
Tue 1-Dec-2009 |
Mon 4-Jan-2010 |
4.969% |
5.019% |
Each row represents a
reset period. The first 5 rates come
from the reset table that was input. The
remaining rates are forward rates implied form the accruing curve.