The Garman Kohlhagen Model

Overview

The Garman Kohlhagen model is suitable for evaluating European style options on spot foreign exchange. This model alleviates the restrictive assumption used in the Black Scholes model that borrowing and lending is performed at the same risk free rate. In the foreign exchange market there is no reason that the risk free rate should be identical in each country. Any interest rate differential between the two currencies will impact the value of the FX option. The risk free foreign interest rate in this case can be thought of as a continuous dividend yield being paid on the foreign currency. Since an option holder does not receive any cash flows paid from the underlying instrument, this should be reflected in a lower option price in the case of a call or a higher price in the case of a put. The Garman Kohlhagen model provides a solution by subtracting the present value of the continuous cash flow from the price of the underlying instrument. Assumptions under which the formula was derived include:

· the option can only be exercised on the expiry date (European style);

· there are no taxes, margins or transaction costs;

· the risk free interest rates (domestic and foreign) are constant;

· the price volatility of the underlying instrument is constant; and

· the price movements of the underlying instrument follow a lognormal distribution.

Formulas & Technical Details

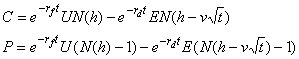
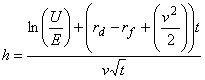
where

= theoretical Value of a Call

= theoretical value of a put

= price of the underlying

= exercise price

= time to expiration in years

= annual volatility in percent

= risk free interest rate in the domestic currency

= risk free interest rate in the foreign currency

= base of the natural logarithm

= natural logarithm

= cumulative normal density function

FINCAD Functions

aaGK (FX_spot, ex, d_exp, d_v, vlt, rate_dom_ann, rate_for_ann, option_type, stat, acc_dom, acc_for)

This FINCAD function can be used to work with European style options on spot foreign exchange.

Description of Inputs

Input Argument	Description
FX_Spot	FX spot – domestic/foreign
ex	exercise price
d_exp	expiry date
d_v	value (settlement) date
vlt	volatility
rate_dom_ann	rate – domestic - annual
rate_for_ann	rate – foreign – annual
option_type	option type, 1=call, 2=put
stat	list of statistics; refer to Description of Outputs
acc_dom	accrual method – domestic rate
acc_for	accrual method – foreign rate

Description of Outputs

Output Statistic	Description
1	fair value
2	delta
3	gamma
4	theta
5	vega
6	rho of domestic rate
7	rho of foreign rate

For details about the calculation of Greeks, see the Greeks of Options on non-Interest Rate Instruments FINCAD Math Reference document.

Example

Your base currency is US and you need to buy a 90 day put on the British Pound. You will be dealing with a bank and the put offered will be European style exercise. You have completed a review of the historical volatility of the Pound and 15% is your guess of where it should be for now. The 3 month Eurodollar rate is 6.06% (accrual method is actual/360) and the 3 month EuroSterling rate is 11.68% (accrual method is actual/365 fixed). The US dollar closed last night at 1.7535 per pound and you want your put to have a strike of 1.7506. What is the fair value of this put?

aaGK

Argument	Description	Example Data	Switch
FX_spot	spot price of underlying currency (domestic : foreign)	1.7535
ex	exercise price	1.7506
d_exp	expiry date	16-Mar-1994
d_v	settlement date	24-Sep-1993
vlt	annual volatility estimate	0.15
rate_dom_ann	domestic riskless deposit rate	0.0606
rate_for_ann	foreign riskless deposit rate	0.1168
option_type	option type	2	put
stat	list of statistics	1	fair value (domestic : foreign)
acc_dom	method of interest accrual for the domestic rate	2	actual/ 360
acc_for	method of interest accrual for the foreign rate	1	actual/ 365 (fixed)

Results

Statistics	Description	Value
1	fair value (domestic/foreign)	0.089802467

The fair value of the put is $.090 per pound sterling.

The function utilizes the following conventions:

· The foreign exchange rate used in the function must be input on a “units of domestic per one unit of foreign” basis. This may or may not conform with the currencies you are working with since both direct and indirect quotes are used in the market place. If the currencies are quoted as “units of foreign per one unit of domestic” basis, simply take the inverse of the FX price and use this price in the function.

· Output from the function is always returned in terms of the domestic currency. For example, if the FX spot price was input as Yen/USD, the option price would be in terms of Yen per unit of foreign currency (e.g. USD) as we have assumed the domestic currency to be Yen. Multiply this option price by the notional contract amount to get the value of the position in Yen. Convert this Yen amount into dollars by the current FX spot rate.

· Finally, the rates used in the Garman Kohlhagen model are assumed to be input as annual compounded rates (e.g. (1+rate)^t). This rate is then converted into a continuously compounded rate inside the closed form model. If your input rate is quoted on a simple interest rate basis (e.g. money market rate), or compounded on a different compounding frequency (e.g. bond basis), convert these rates to an annual compounding basis prior to using as direct inputs to the function.

References

[1] Bookstaber, Richard, (1991), Option Pricing and Investment Strategies 3rd Edition, Probus Publishing Company.

[2] Cox, John; Rubinstein, Mark, (1985), Options Markets, Prentice Hall.

[3] ‘From Black Scholes to Black Holes’, Risk, 1994.

[4] Hull, John, (1993), Options Futures and other Derivative Securities 2nd Edition, Prentice Hall.

[5] Natenburg, Sheldon, (1988), Option Volatility and Pricing Strategies, Probus Publishing Company.

Disclaimer

With respect to this document, FinancialCAD Corporation (“FINCAD”) makes no warranty either express or implied, including, but not limited to, any implied warranty of merchantability or fitness for a particular purpose. In no event shall FINCAD be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of the use of this document or the information contained in it. This document should not be relied on as a substitute for your own independent research or the advice of your professional financial, accounting or other advisors.

This information is subject to change without notice. FINCAD assumes no responsibility for any errors in this document or their consequences and reserves the right to make changes to this document without notice.