LIBOR Market Model

Overview

The LIBOR Market Model (LMM) is an interest rate model based on evolving LIBOR market forward rates.  It is also known as the Brace-Gatarek-Musiela (BGM) model, after the authors of one of the first papers where it was introduced (Ref [2]).  In contrast to models that evolve the instantaneous short rate (Hull-White, Black-Karasinski models) or instantaneous forward rates (Heath-Jarrow-Morton model), which are not directly observable in the market, the objects modeled using LMM are market-observable quantities (LIBOR forward rates).  This makes LMM popular with market practitioners.  Another feature that makes the LMM popular is that it is consistent with the market standard approach for pricing caps using Black’s formula.

The LMM can be used to price any instrument whose pay-off can be decomposed into a set of forward rates.  It assumes that the evolution of each forward rate is lognormal.  Each forward rate has a time dependent volatility and time dependent correlations with the other forward rates.  After specifying these volatilities and correlations, the forward rates can be evolved using Monte Carlo simulation.  Expectations of discounted coupons are then calculated in order to determine the fair value of an instrument.  For more information on the LMM see Brigo and Mercurio [3], Joshi [7] and Hull [4].

The standard lognormal LMM does not produce the market-observed caplet volatility smile/skew (Ref [3]).  To produce a skew, the LMM can be extended to incorporate a local volatility model, a stochastic volatility model, a jump diffusion model, or some combination of the above.  FINCAD provides pricing functions that permit the use of three different versions of the LMM: (1) the standard lognormal LMM, (2) the LMM enhanced with a Constant Elasticity of Variance (CEV) local volatility process, and (3) the LMM enhanced with a Displaced Diffusion (DD) local volatility process.  The next section discusses the standard lognormal LMM in detail.  A sub-section at the end discusses the local volatility extensions.

Formulas & Technical Details

Lognormal LIBOR Market Model

Assume that there are  forward rates  that describe the pay-off of an interest rate derivative.  The evolution of each forward rate  is described by the stochastic differential equation:

Equation 1

where

 is a standard Wiener process and

 is the instantaneous correlation between forward rates  and . 

The instantaneous lognormal volatility and drift of forward rate  are  and , respectively.  Note that the drift  for forward rate  can be calculated from the other forward rates and their instantaneous volatilities and correlations (see Joshi for more details Ref [7]).  Thus, the instantaneous volatilities and correlations completely describe how forward rates will evolve in the future.  The first thing to do is to specify the instantaneous volatilities and correlations.

There are three main approaches for determining the instantaneous volatilities and correlations of forward rates (Ref [12]):

1.       They can be obtained from analyzing historical data.

2.       They can be obtained by calibrating the model to current market prices of caplets and European swaptions.

3.       The user can explicitly specify volatilities and correlations based on how he or she believes they will evolve in the future.

A combination of these three approaches can also be used.

Calibration

FINCAD provides functions for calibrating (see the Calibration FINCAD Math Reference document) the instantaneous volatilities and correlations of the LMM to quoted market data for caplets and European swaptions.  The calibration of the LMM is a delicate issue and is still an area of active research (Refs [3], [12], [13]).  Calibrating time-dependent instantaneous volatilities and correlations of a set of forward rates to market data can be a difficult task. 

To simplify the calibration procedure, the LMM calibration functions use restricted functional forms (presented in recent literature Refs [3], [7], [6]) for the instantaneous volatilities and correlations.  The trade-off in using restricted functional forms to make the calibration procedure easier is that they may not be able to fit all market conditions.  By calibrating using restricted functional forms, the approach taken is really a combination of approaches 2 and 3 as discussed in the previous section.  This is because choosing a functional form limits how forward rates can evolve in the future.  Even though calibration is performed on market data, the choice of the functional form places restrictions on how the rates can evolve.

The FINCAD LMM calibration functions use the following functional form (or parameterization) for the instantaneous volatilities of forward rates:

Equation 2

This linear-exponential parametric form is a time-homogeneous form, which means that the instantaneous volatility of a forward rate is not a function of the current date but only a function of the time until the rate is set. The parameters  allow for the exact fitting of specific forward rate volatilities to quoted caplet volatilities. This parametric form is able to produce both a monotonically decreasing and “humped” structure of the instantaneous volatility, consistent with features observed in the market. In addition, the parameters  can be interpreted in financial terms. For very long maturities i.e. when  is large, the instantaneous volatility approaches . Therefore we can interpret  as the volatility of forward rates very far in the future. Generally, this parameter should have a positive value. The parameter  can be interpreted as the rate at which the volatility approaches the limit . For forward rates with very short maturities, i.e. when  approaches zero, we can see the instantaneous volatility approaches . This leads us to conclude that this quantity should also be greater than zero. We can gain some insight into the location of the hump in the volatility structure by evaluating From this we find that the hump is located at  Therefore, a hump will only be present for Under normal circumstances, we observe a volatility structure similar to the one shown in the Figure 1 (using parameter values from Joshi [7] and Jaeckel [6]). The initial positive slope allows us to infer the further restriction that  in this case. For more details see Brigo and Mercurio [3], Joshi [7] and Jaeckel [6].

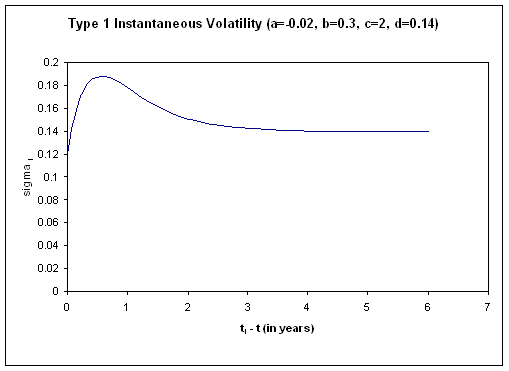
Figure 1

The FINCAD LMM calibration functions use the following functional form (or parameterization) for the instantaneous correlations between forward rates:

Equation 3

This exponential parametric form is not time dependent (i.e., it does not depend on the current date nor the times until the two forward rates are set, but only on the difference between the two times).  It is discussed by Molgedey [9].  It is also a more general case of forms presented by Joshi [7] and Jaeckel [6].  The figure below shows the instantaneous correlation for some parameter values used by Joshi [7] and Jaeckel [6].  The general interpretation of this structure is that forward rates with similar maturities show a high degree of correlation, while those with very different maturities are less correlated. We see that when , the correlation is 1 as required. The parameter  can be interpreted as the limit of instantaneous correlation that is approached for rates far separated in time, while the parameter  describes how fast the correlation decreases and approaches . In terms of an instantaneous correlation matrix, this parametric form describes a matrix with ones along the diagonal and values decreasing at a rate of  as we move away from the diagonal. The limit that the far off-diagonal elements approach is given by .

It should be noted that the above specification of the instantaneous correlation between forward rates does not entirely describe the “terminal correlation” between the rates. i.e. the non-instantaneous correlation. The terminal correlation is determined by a combination of both the instantaneous volatility and correlation structures. See Brigo and Mercurio [3] for more details.

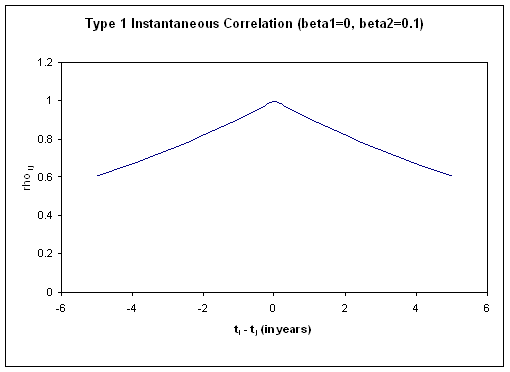
Figure 2

The FINCAD LMM calibration functions allow:

·         a functional form for instantaneous volatilities to be fitted to caplet data (caplet data contains no information about correlations).

·         a functional form for instantaneous correlations to be fitted to European swaption data given a specified form for instantaneous volatilities (obtained from calibration to caplets).

·         functional forms for both instantaneous volatilities and correlations to be fitted simultaneously to European swaption data alone.

For example, the FINCAD calibration functions allow a user to calibrate the instantaneous volatility and correlation parameters by (1) calibrating the volatility parameters , and  to caplet data; then (2) holding these parameters fixed while calibrating the instantaneous correlation parameters  and  to swaption data (see the Calibration FINCAD Math Reference document for more information).

The exact procedure by which caplets and swaptions are used to calibrate the instantaneous volatilities and correlations depends on the particular pricing application.  For example, one practitioner (Ref [6]) does not calibrate the instantaneous correlations at all.  Rather, the correlation parameters are set to values based on historical data.  The volatility parameters ,  are calibrated to caplet data, then a forward rate-forward rate covariance matrix is constructed (see Equation 4 below).  This matrix is transformed into a swap rate-swap rate covariance matrix, which is then calibrated to swaption data.  In this way one obtains a “calibration to European swaption prices whilst retaining as much calibration to the caplets as possible without violating the overall FRA/FRA correlation structure too much, which is typically exactly what a practitioner wants for the pricing of Bermuda swaptions” (Ref [6]).  A similar procedure using the FINCAD functions would be to (1) set the instantaneous correlation parameters  and  to values suggested in the literature (, see Ref [6]); (2) use the FINCAD functions to calibrate the instantaneous volatility parameters , and ; to caplet data; then (3) use the FINCAD functions to calibrate the instantaneous volatility and correlation parameters , , and  to swaption data, using a narrow range of allowed values for each parameter centered on the values determined in steps (1) and (2) (see the Calibration FINCAD Math Reference document for more information).

Calibrated values of the lognormal volatility and correlation parameters typically lie in the ranges:

·         : -1 to 1

·         :  0 to 0.5

·         :  0 to 5

·         :  0 to 0.5

·         : 0 to 1

·         : 0 to 1

The performance of the calibration functions with respect to determining volatility and correlation parameters depends on the characteristics and quality of the caplet and swaption data.  For example, calibration using illiquid or inaccurate data (see Refs [3], [13]) may result in function failure or incorrect parameter values.  Also, because the calibration functions use restricted parametric forms for instantaneous volatilities and correlations, there will be cases when the functions fail even when the market data is liquid and accurate.  In these cases, users will have to use a combination of the three approaches (described at the end of the previous section) for determining volatilities and correlations.

In order to make the calibration functions more efficient, closed form approximations are used to price European swaptions that do not require Monte Carlo simulation.  Note that caplets can already be priced easily with LMM (see Joshi [7] and Jaeckel [6]).  Two closed-form approximations are implemented for pricing European swaptions in LMM: one proposed by Rebonato and one proposed by Hull and White.  These are described in detail in Brigo and Mercurio [3].  The LMM swaption calibration function uses these closed-form approximations to price European swaptions.

Pricing

Evolving the Forward Rates using Monte Carlo Simulation

After specifying which forward rates to evolve and their instantaneous volatilities and correlations, by calibration or other means, a Monte Carlo simulation can be performed to price the instrument.  The first step is to evolve the forward rates from the value date to each date the pay-off of the instrument depends on.  This is done by numerically integrating Equation 1 using the predictor-corrector technique for solving ordinary differential equations as described by Jaeckel [6].

In particular, an  covariance matrix  is built for each user-defined forward rate evolution period, where  is the number of forward rates.  For example, given that  is the forward rate effective at  and terminating at , then for the time period , where , the elements of the  instantaneous covariance matrix are:

.

Equation 4

The covariance matrix  contains all the information needed to evolve the forward rates from time  to  and can be calculated from the restricted functional forms for instantaneous volatilities and correlations.  In particular, the parameterization of instantaneous correlation in Equation 3 is time-independent, which means that instantaneous correlation can be taken out of the covariance integral in Equation 4.  The resulting integral can be evaluated analytically using the functional form for instantaneous volatility from Equation 2 (see Jaeckel [6]).

If the pay-off of the instrument depends on the value of the forward rates  at one future time , the forward rates only have to be evolved for a single time step from the value date  to .  This requires only a single  covariance matrix for time period t0 to t1 to describe the evolution of forward rates.  If the payoff of the instrument depends on the forward rates observed at  dates , , … , the forward rates need to be evolved for m time steps from 0 to ,  to , …  to .  To specify the evolution of forward rates requires  separate covariance matrices, one for each time evolution period.

Given the matrix elements  for a particular time evolution period,  is decomposed into a pseudo square root via the Cholesky method, or via spectral decomposition if the Cholesky method fails for any reason:

.

Equation 5

 Equation 1 is then written as (Ref [6]):

Equation 6

where the  are  independent Wiener processes.  If one wishes to employ “factor reduction” and evolve the forward rates using  independent Wiener processes (Ref [6]), then Equation 1 is re-written as:

.

Equation 7

The variances of the forward rates, , (obtained from calibration or directly from the market-quoted implied volatilities of caplets) are retained by setting (Ref [6]):

.

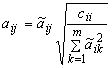Equation 8

The FINCAD implementation of the LMM uses the zero coupon bond maturing at time  (i.e., on the terminating date of the  forward rate, ) as numeraire, so the drift of  at time  is given by (Refs [3], [6]):

.

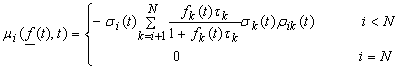Equation 9

 is the accrual factor for the rate term defined by .

Because the drifts given by Equation 9 are state dependent and therefore indirectly stochastic, Equation 1 must be solved using a numerical scheme.  FINCAD implements a log-Euler discretization of the forward rate process (Refs [3], [6]):

.

Equation 10

 is the drift from Equation 9, predicted using Equation 4 for the period , then corrected using the “predictor-corrector” method (Ref [6]) to take into account the fact that the  change during the evolution period.

Forward rates in the standard lognormal LMM are evolved over successive time periods in a Monte Carlo simulation according to Equation 10, given the forward rate-forward rate covariance matrix  for each time period.  By generating many such paths of forward rates, the expectation of a particular forward rate on a particular date in the chosen probability measure (i.e., the -forward measure or terminal measure), conditional on today’s value of the forward rate, is the average simulated value over all paths.  On each path of forward rates, the coupons and the price of the numeraire asset are calculated on coupon payment dates.  Today’s value of the numeraire asset is also calculated for the path.  The coupons are discounted through the numeraire and summed to get the price of the instrument on the path.  The fair value of the instrument is found by averaging over all paths.

User Defined Covariance Matrices

An input to the FINCAD interest rate derivative pricing functions that use the LMM is a sequence of covariance matrices, one for each time evolution period of the instrument.  Utility functions are provided to generate these covariance matrices, given the parametric forms for instantaneous volatilities and correlations described above. 

Instead of using the calibration and matrix generation functions, users can define their own covariance matrices and input them directly into the pricing functions.  The following example describes how this can be done.

The example assumes an instrument whose pay-off depends on 4 forward rates.  The first forward rate  is from , the second forward rate  is from , the third forward rate  is from , the fourth forward rate  is from  and the current date corresponds to time .  Also, suppose this instrument has a Bermudan structure and its pay-off depends on the forward rates observed at times , and .  Running the simulation requires evolving the forward rates from , ,  and .  Thus, four separate 4 by 4 covariance matrices are required to describe the evolution of forward rates, one for each time step that needs to be evolved.

Now, suppose the user wants to explicitly specify the instantaneous volatilities and correlations as piece-wise constant functions (i.e., and  are constants during each time step) with the following values:

From t0 to t1,


From t1 to t2,


From t2 to t3,


From t3 to t4,


Notice that the data has a certain structure.  For each time period  and  if .  This is because for i forward rate  has already expired because it is already past its starting time .  Forward rates that have already expired cannot be evolved so they do not have volatilities and correlations.  So for this example, from , the forward rates  have to be evolved; from , forward rates  have to be evolved; from , forward rates  have to be evolved; and from , only  has to be evolved.

Also, notice that the non-zero diagonals of the instantaneous correlation matrix are always one and the matrix is symmetric. This is because the correlation between  and  is the same as that between  and .  Another restriction on the instantaneous correlation matrix is that is it positive definite.  For more on restrictions for instantaneous volatilities and correlations, see Ref [3].

Given values for the instantaneous volatilities and correlations, Equation 4 is then used to generate the covariance matrices.  Because the instantaneous volatilities and correlations are piecewise-constant, the integral is easy to evaluate.  For example, to calculate the entry  suppose that  and  (in years).  From Equation 4,  using the values of  between  and .  Thus, .

Early Exercise in Monte Carlo Simulation

When there is only one possible exercise date (European exercise), Monte Carlo pricing is a straightforward procedure (see Ref [8]).  When there are multiple possible exercise dates (Bermudan exercise), Monte Carlo pricing is more difficult.  The Monte Carlo method propagates forward rates forward in time.  However, one needs to know about the future in order to determine whether or not it is optimal to exercise the option now, or hold the option until a later exercise date.  One needs to know both the “exercise value” and the “continuation value” of the option on a given date of a Monte Carlo path of simulated forward rates.  The continuation value is the expectation of future exercise values.  Additional steps must be taken in the Monte Carlo simulation to calculate this expectation. 

The FINCAD LMM implementation uses the Least Squares Monte Carlo (LSMC) algorithm proposed by Longstaff and Schwartz [8] to price instruments with early exercise features.  The LSMC algorithm works backwards from the last exercise date to previous exercise dates as follows:

1.       Calculate the exercise value on the exercise date for each path.  For Bermudan swaptions, the exercise value is simply the value of the underlying swap, which is easily calculated “off the curve” (Ref [12]).

2.       If this is the last exercise date, set the continuation value = discounted continuation value = 0 for each path and go to Step 6.

3.       For each path, set the continuation value on the exercise date equal to the discounted continuation value from the later exercise date.

4.       Regress the continuation values from each path in Step 3 against a linear combination of “basis functions” evaluated at “regression variables”.

5.       Use the regression parameters, regression variables, and basis functions from Step 4 to estimate the continuation value on the exercise date for each path.

6.       For each path, if the exercise value > continuation value, then set the exercise flag for this date = TRUE and set continuation value = exercise value.  Otherwise, set the exercise flag = FALSE and set continuation value = discounted continuation value.

7.       Move to the previous exercise date.

8.       Repeat steps 1-7 until there are no more exercise dates.

The earliest date on each path for which exercise flag = TRUE is the optimal exercise date for that path. 

The exercise strategy found by the LSMC algorithm is typically a sub-optimal exercise strategy (at best, the optimal exercise strategy), so the price of the option given by the LSMC algorithm is a lower bound on the price.

The choice of regression variables and choice of basis functions affect how closely the LSMC algorithm approximates the optimal exercise strategy, and depend on the specific instrument being priced (Refs [8], [12]).  The FINCAD pricing functions provide a choice between two sets of regression variables:  either the 0th and 1st moments of the interest rate curve (i.e., the level and slope of the interest rate curve, represented by a swap price per unit notional and a forward rate) or the sums of the random factors used to evolve each forward rate.  A choice between two different sets of basis functions is also provided:  either 2nd-order polynomials or 2nd-order Laguerre polynomials.  The price of an instrument, e.g., a Bermudan swaption, is not expected to be particularly sensitive to the basis functions.  Instead, one should focus on selecting regression variables that are indicative of continuation values relative to exercise values (Ref [12]).  The sums of random factors are general variables that can be used for any derivative.  In the case of swaptions, the 0th and 1st moments of the interest rate curve are expected to be the best choice for regression variables.  For more details on the choice of regression variables and basis functions for Bermudan swaptions see Pedersen [11] and Piterbarg [12]. 

The LSMC algorithm is described further in the Bermudan and American Style Basket Options FINCAD Math Reference document.

Local Volatility Extensions

FINCAD provides two local volatility extensions to the LMM in order to model implied volatility skew:  Constant Elasticity of Variance (CEV) and Displaced Diffusion (DD).

Constant Elasticity of Variance

In the LMM with CEV, Equation 1 becomes (Refs [5], [10], [14]):

Equation 11

so that Equation 9 becomes (Refs [1], [5], [10]):

.

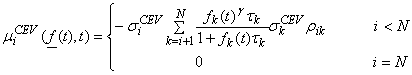Equation 12

and Equation 10 becomes (Refs [1], [5], [10]):

Equation 13

where  is the CEV parameter, constant for all forward rates.  That is, forward rates in the LMM+CEV are evolved over successive time periods in a Monte Carlo simulation according to Equation 13, given  and the forward rate-forward rate CEV covariance matrix for each time period.  The parameterization of CEV instantaneous volatility and correlation for calibration of the covariance matrix retain the same forms as shown in Equation 2 and Equation 3, respectively.  The standard LMM is recovered from the LMM+CEV by simply setting .

Note that Equation 13 is the log-Euler discretization of Equation 11.  In a process such as CEV where forward rate = 0 is possible, it is typically better to use a direct Euler discretization of the stochastic differential equation (Ref [1]).  However, for typical market conditions where forward rate = 0 is improbable, the log-Euler discretization works well.

Closed-form expressions for the prices of caplets and European swaptions are available (Refs [1], [3], [5], [10]) for calibration of the LMM+CEV.  Typical values of the calibrated model parameters are , , , and  for a negative skew (caplet implied volatility decreases with strike rate), or , , , and  for a positive skew (caplet implied volatility increases with strike rate).  When calibrating the LMM+CEV, one must usually input large uncertainties for the calibration instruments (caplets or swaptions) that are far from the money (see the Calibration FINCAD Math Reference document), because these instruments have near-zero vega which means the same price is obtained for a large range of volatilities.

Displaced Diffusion

In the LMM with DD, Equation 1 becomes (Refs [7], [10], [14]):

Equation 14

so that Equation 9 becomes (Refs [1], [7], [10]):

.

Equation 15

and Equation 10 becomes (Refs [1], [3], [10], [14]):

Equation 16

where  is the DD parameter, constant for all forward rates.  That is, forward rates in the LMM+DD are evolved over successive time periods in a Monte Carlo simulation according to Equation 16, given  and the forward rate-forward rate DD covariance matrix for each time period.  The parameterization of DD instantaneous volatility and correlation for calibration of the covariance matrix retain the same forms as shown in Equation 2 and Equation 3, respectively.  The standard LMM is recovered from the LMM+DD by simply setting  = 0.

Closed-form expressions for the prices of caplets and European swaptions are available (Refs [3], [10]) for calibration of the LMM+DD.  Typical values of the calibrated model parameters are , , , and  for a negative skew (caplet implied volatility decreases with strike rate), or , , , and  for a positive skew (caplet implied volatility increases with strike rate).  When calibrating the LMM+DD, one must usually input large uncertainties for the calibration instruments (caplets or swaptions) that are far from the money (see the Calibration FINCAD Math Reference document), because these instruments have near-zero vega which means the same price is obtained for a large range of volatilities.

FINCAD Functions

 

aaCovarMatGen2_LMM (d_v, period_date_tbl, fwdrate_tbl, acc, model_vol, model_cor, model_parms, scalfac_tbl)

Generates a sequence of forward rate - forward rate covariance matrices using the LIBOR Market Model.  The covariance matrices are used to evolve forward rates over sequential time periods.  Functional forms are used for instantaneous volatilities and correlations.

 

aaSwaption_eu_LMM (d_v, fwdrate_tbl, npa, cpn, acc, swpn, df_crv, intrp, approx, covar_mat, stat)

Calculates the fair value for a European style swaption using the LIBOR Market Model with closed form analytic approximations.

 

aaSwaption2_eu_LMM_ff (d_v, d_e, d_m, princ, cpn, freq, acc, d_rul, swpn, hl, approx, model_vol, model_cor, model_parms, scalfac_tbl, df_crv, intrp, stat)

Calculates fair value for a European style swaption using the LIBOR Market Model with local volatility.  Closed-form analytic approximations are used for valuation, and functional forms are used for instantaneous volatilities and correlations.

 

aaCaplet_LMM(r_option_type, princ, d_v, d_exp, d_e, d_t, rate_ex, acc, model_vol, model_parms, scalfac_tbl, df_crv, intrp, stat)

Calculates fair value of a caplet or floorlet using the LIBOR Market Model with local volatility.

 

aaCapletVltGen_LMM(d_v, d_e, acc, vol_tbl, scale_fact)

Generates the Black volatility of a caplet or floorlet using a functional form for the instantaneous volatility in the LIBOR Market Model.

 

aaSwaption_LMM_fs(d_v, swap_tbl, acc_pay, acc_rate, swpn, df_crv, intrp, covar_mat, num_fact, reg_var, basis_fn, num_rnd, table_type)

Calculates the fair value of a Bermudan style swaption with the LIBOR Market Model using Monte Carlo simulation.  Allows for known resets, setting of rate in-advance or in-arrears, and time-varying notionals, coupons, margins, and exercise fees.

 

aaSwaption_LMM_LV_fs(d_v, swap_tbl, acc_pay, acc_rate, swpn, df_crv, intrp, covar_mat, num_fact, lv_model, lv_param, reg_var, basis_fn, num_rnd, table_type)

Calculates the fair value of a Bermudan style swaption with the LIBOR Market Model and local volatility using Monte Carlo simulation.  Allows for known resets, setting of rate in-advance or in-arrears, and time-varying notionals, coupons, margins, and exercise fees.

 

aaSwaption_LMM_fs_tbl(d_v, swap_tbl, table_type)

Generates a table of rate evolution periods or rate terms for a swaption.

 

Description of Inputs

Input Argument

Type

Description

d_v

Date

Valuation (Settlement) Date.

d_e

Date

Effective Date.

d_m

Date

Maturity Date.

d_t

Date

Terminating Date.

d_exp

Date

Expiry Date.

npa, princ

Number

Notional Principal Amount.

cpn

Number

Coupon Rate.

freq

Number

Frequency.

acc, acc_pay, acc_rate

Number

Day Count Convention.

r_option_type, swpn

Number

Option Type.

rate_ex

Rate

Exercise Rate.

d_rul

Number

Business Day Convention.

swpn

Number

Specify as either a payer or receiver swaption.

hl

Table

Holiday List.

df_crv

Table

Discount Factor Curve.

intrp

Number

Interpolation Method.

model_vol

Number

Parameterization of instantaneous volatility.

model_cor

Number

Parameterization of instantaneous correlation.

model_parms

Table

Table containing values of instantaneous volatility and correlation parameters.

scalfac_tbl

Table

Volatility scale factor table for forward rates.  This table can be entered as a 3-column table (effective date, terminating date, scale factor) or as a single cell containing a single scale factor that is applied to the model-predicted volatilities of all forward rates.

scale_fact

 

Volatility scale factor for a single forward rate.

vol_tbl

Table

Table specifying the parameters for a functional form of instantaneous volatility.

swap_tbl

 

Swap coupon table.  This is an N×9 table, where the columns are rate effective date, rate terminating date, coupon effective date, coupon terminating date, notional principal amount, coupon, margin above or below a floating rate, exercise flag, and exercise fee (% of notional).  The dates must be input already adjusted for holidays, weekends, and a business day convention.  All rates are input as annualized rates.

 

Each row of the swap table corresponds to a coupon period. The columns of the table are specified as follows:

1.       Both rate terms and coupon periods must be contiguous. That is, the terminating date in one row of the table must be the effective date in the next row of the table.

2.       There is one rate per coupon period.  The rate effective date must be on or before the coupon terminating date.  The rate can set in advance or in arrears by adjusting the rate effective and terminating dates relative to the coupon effective and terminating dates.  In-arrears pricing is handled via Monte Carlo evolution of forward rates to the rate effective dates and coupon terminating dates.  No extra timing or convexity adjustments are required.

3.       A forward rate is evolved in Monte Carlo if rate effective date > value date.

4.       The coupon periods apply to both the fixed and floating legs of the swap.

5.       The coupon is the annualized rate on the fixed leg; the margin is the annualized margin on the floating leg.

An exercise flag > 0 means that the option to enter the underlying swap is exercisable on the coupon effective date.

lv_model

Number

Local volatility model.

lv_param

Number

Local volatility parameter.

period_date_tbl

Table

Table containing starting and end dates for a set of time periods to generate covariance matrices for the forward rates.

fwdrate_tbl

Table

Table containing effective and terminating dates for a set of forward rates.

covar_mat

Table

Table containing a covariance matrix (or sequence of covariance matrices) describing the evolution of a set of forward rates.

approx

Number

Approximate closed-form expression for valuing a European swaption in the Libor Market Model.

num_fact

Number

Maximum number of factors to use in Monte Carlo simulation.

reg_var

Number

Choice of regression variables in LSMC algorithm.

basis_fn

 

Choice of basis functions in LSMC algorithm.

num_rnd

Table

Number of Monte Carlo paths.  If this number is an integer, a random seed is used to generate random numbers.  Otherwise, a fixed seed is used.

stat

Number

Statistic to be output.

table_type

Number

Type of table to output.

 

Description of Outputs

aaCovarMatGen2_LMM

Output

Type

Description

covar_mat

Table

Table containing a sequence of covariance matrices

aaSwaption_eu_LMM, aaSwaption2_eu_LMM_ff

Output Statistics

Type

Description

1

Number

option price

2

Rate

swaption Black volatility

3

Rate

par swap rate

aaCaplet_LMM

Output Statistics

Type

Description

1

Number

caplet/floorlet price

2

Rate

caplet/floorlet Black volatility

3

Rate

implied forward rate

aaCapletVltGen_LMM

Output

Type

Description

caplet_vol

Number

caplet Black volatility

aaSwaption_LMM_fs, aaSwaption_LMM_LV_fs

table_type = 1, ROW 1 = average over all paths, ROW 2 = accuracy

Column

Type

Description

1

Number

Option price

2

Number

Expected time of exercise (in years)

3

Number

Probability of exercise

aaSwaption_LMM_fs_tbl

table_type = 1

Column

Type

Description

1

Date

Effective date of evolution period

2

Date

Terminating date of evolution period

table_type = 2

Column

Type

Description

1

Date

Effective date of rate term

2

Date

Terminating date of rate term

 

Example

Valuation of Bermudan Swaptions

This example shows how to value a Bermudan swaption in the LMM using aaSwaption_LMM_fs.  The flow of data through the FINCAD functions is shown in Figure 3.

Note that the flow of data for aaSwaption_LMM_LV_fs, which uses the LMM enhanced with local volatility, is identical to that shown in Figure 3 except that (1) aaSwaption_LMM_fs is replaced by aaSwaption_LMM_LV_fs; (2) aaCalibrateRCap3 and aaCalibrateSwaption2_LMM output an additional parameter, namely, the local volatility parameter, gamma; (3) gamma is input directly into aaSwaption_LMM_LV_fs.  The other model parameters (a, b, c, d, beta1, beta2) are still input into aaCovarMatGen2_LMM in order to produce the sequence of covariance matrices.

Figure 3:  Data flow through FINCAD functions in order to price a Bermudan swaption using the LIBOR Market Model.

Assume the Bermudan swaption being valued has settlement date of 14-Feb-2000, an effective date of 15-Mar-2000 and a maturity date of 15-Mar-2004.  An accrual method of 30/360, no business day adjustments and linear interpolation are used for all calculations.  The fixed and floating payments are both annual, the principal amount is 100, the fixed coupon is 5.0% and the swaption is the right to receive fixed.

First we generate the rate terms and coupon periods using aaDateGen with the following inputs:

aaDateGen

Argument

Description

Example Data

Switch

d_s

settlement date

14-Feb-2000

 

d_t

terminating date

15-Mar-2004

 

d_e

effective date

15-Mar-2000

 

d_f_cpn

date of first coupon after effective date

omitted

 

d_l_cpn

date of last coupon prior to terminating date

omitted

 

freq

cash flow frequency

1

annual

hl

holiday list

empty (for simplicity)

 

d_rul

business day convention

1

no date adjustment

table_type

table type

2

two-column array

The output rate terms and coupon periods are:

 Output Table 1 – rate terms/coupon periods

Effective Date

Terminating Date

15-Mar-2000

15-Mar-2001

15-Mar-2001

15-Mar-2002

15-Mar-2002

15-Mar-2003

15-Mar-2003

15-Mar-2004

Given the coupon periods and rate terms, we build the swap table:

t_1225 – swap table

rate eff date

rate term date

coupon eff date

coupon term date

NPA

cpn

margin

ex flag

ex fee

15-Mar-2000

15-Mar-2001

15-Mar-2000

15-Mar-2001

100

5.0%

0.0%

1

0.0%

15-Mar-2001

15-Mar-2002

15-Mar-2001

15-Mar-2002

100

5.0%

0.0%

1

0.0%

15-Mar-2002

15-Mar-2003

15-Mar-2002

15-Mar-2003

100

5.0%

0.0%

1

0.0%

15-Mar-2003

15-Mar-2004

15-Mar-2003

15-Mar-2004

100

5.0%

0.0%

1

0.0%

  We now generate the evolution periods and forward rates for Monte Carlo simulation using aaSwaption_LMM_fs_tbl:

aaSwaption_LMM_fs_tbl

Argument

Description

Example Data

Switch

d_v

value date

14-Feb-2000

 

swap_tbl

swap table

t_1225 (above)

 

table_type

table type

1…2

period dates table or forward rate table

The evolution periods (table_type = 1) and forward rates (table_type = 2) from aaSwaption_LMM_fs_tbl are: 

Output Table 2 – period dates table

Effective Date

Terminating Date

14-Feb-2000

15-Mar-2000

15-Mar-2000

15-Mar-2001

15-Mar-2001

15-Mar-2002

15-Mar-2002

15-Mar-2003

Output Table 3 –forward rate table

Effective Date

Terminating Date

15-Mar-2000

15-Mar-2001

15-Mar-2001

15-Mar-2002

15-Mar-2002

15-Mar-2003

15-Mar-2003

15-Mar-2004

Note that the list of forward rates in Output Table 3 includes all rates from the swap table above (t_1225), because all of these rates set in the future (i.e., after the Value Date).  Also note that there are 4 rate evolution periods in Output Table 2.  To price the swaption, forward rates need to be evolved to each of the rate effective dates.  Rates also need to be evolved to all coupon terminating dates (except the last one) because the swaption is exercisable on these dates.   These swaption exercise dates coincide with the rate effective dates, so we need only consider the rate effective dates when determining the rate evolution periods, which is why there are 4 periods in Output Table 2.

The function aaCovarMatGen2_LMM can be used to generate the sequence of covariance matrices required as an input to aaSwaption_LMM_fs.  Suppose that aaCalibrateSwaption2_LMM has been used to calibrate the LMM to swaptions, with the 4-parameter linear-exponential parametric form for instantaneous lognormal volatilities, the exponential form for instantaneous correlations, and volatility scale factors set to 1 (see the Calibration FINCAD Math Reference document).  Alternatively we could have used aCalibrateRCap3_LMM to calibrate the instantaneous lognormal volatility parameters (), then used aaCalibrateSwaption2_LMM to calibrate the instantaneous correlation parameters ( and ).  The calibrated parameter values are assembled in Output Table 4.

Output Table 4 – Model Parameters

a

b

c

d

beta1

beta2

-0.02

0.3

2

0.16

0.1

0.1

Output Tables 2 through 4 are used by aaCovarMatGen2_LMM to generate the covariance matrices for the Bermudan swaption.  The complete list of inputs to aaCovarMatGen2_LMM is shown below.

 aaCovarMatGen2_LMM

Argument

Description

Example Data

Switch

d_v

Valuation (settlement) date

14-Feb-2000

 

period_date_tbl

Table containing starting and end dates for a set of time periods

Output Table 2 (above)

 

fwdrate_tbl

Table containing effective and terminating dates for a set of forward rates

Output Table 3 (above)

 

acc

Day count convention

4

30/360

model_vol

Parameterization of instantaneous volatility

1

4-parameter linear exponential

model_cor

Parameterization of instantaneous correlation

1

2-parameter exponential

model_parms

Table containing values of all model parameters

Output Table 4 (above)

 

scalfac_tbl

Volatility scale factor table for forward rates.

1

 

Output Table 5 shows the sequence of four 4x4 covariance matrices generated by aaCovarMatGen2_LMM, which is used to evolve the 4 forward rates over the 4 time periods.

Output Table 5 – Covariance Matrix Sequence

0.00202425

0.00236746

0.00187570

0.00163840

0.00236746

0.00332062

0.00262800

0.00229292

0.00187570

0.00262800

0.00248774

0.00216844

0.00163840

0.00229292

0.00216844

0.00226080

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.03864862

0.03258181

0.02709047

0.00000000

0.03258181

0.03333816

0.02760589

0.00000000

0.02709047

0.02760589

0.02736581

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.03864862

0.03258181

0.00000000

0.00000000

0.03258181

0.03333816

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.00000000

0.03864862

Finally we call aaSwaption_LMM_fs.  We select 2nd order polynomials as basis functions and the 1st two moments of the interest rate curve as regression variables (as described under Formulas & Technical Details above).  We use all possible random factors, which in this case is 4 (the maximum number of stochastic rates in any one period is 4) and we use 1000 Monte Carlo paths with a fixed seed.  The discount factor curve and other inputs are listed below.

t_43_32 – discount factor curve

grid date

discount factor

14-Feb-2000

1.00000000

15-Feb-2000

0.99986634

15-Aug-2000

0.97583485

15-Feb-2001

0.95212637

15-Aug-2001

0.92936652

15-Feb-2002

0.90678702

15-Aug-2002

0.88511098

15-Feb-2003

0.86360669

15-Aug-2003

0.84296283

15-Feb-2004

0.82248256

15-Aug-2004

0.80271444

15-Feb-2005

0.78321202

15-Aug-2005

0.76448994

15-Feb-2006

0.74591621

15-Aug-2006

0.72808566

15-Feb-2007

0.71039639

15-Aug-2007

0.69341491

15-Feb-2008

0.67656799

15-Aug-2008

0.66030689

15-Feb-2009

0.64426435

15-Aug-2009

0.62886370

15-Feb-2010

0.61358509

15-Aug-2010

0.59891781

14-Feb-2011

0.58439810

14-Feb-2012

0.55648080

14-Feb-2013

0.52982607

14-Feb-2014

0.50451573

14-Feb-2015

0.48041449

aaSwaption_LMM_fs

Argument

Description

Example Data

Switch

d_v

value (settlement) date

14-Feb-2000

 

swap_tbl

swap table

t_1225 (above)

 

acc_pay

accrual method for coupon periods

4

30/360

acc_rate

accrual method for rate terms

4

30/360

df_crv

discount factor curve

t_43_32 (above)

 

intrp

interpolation method

1

linear

covar_mat

covariance matrix

Output Table 5 (above)

 

num_fact

maximum number of stochastic factors per period

4

 

reg_var

regression variables

1

IR curve moments

basis_fn

basis functions

1

polynomial

num_rnd

number of random trials

1000.5

 

table_type

table type

1

price table

The output price table, showing price (1st row) and accuracy (2nd row) is:

Output Table 6 – price table

Option price

Expected time of exercise (in years)

Probability of exercise

1.181049

2.447973

0.575075

0.113669

0.128543

0.037544

The 95% confidence interval for the option price is:

[1.181049 – 0.113669, 1.181049 + 0. 113669] = [1.067381, 1.294718].

Accuracy values can be made smaller by increasing the number of Monte Carlo paths (accuracy values decrease roughly in proportion to √P, where P is the number of paths).

 

Related Functions

aaCalibrateRcap2_LMM, aaCalibrateRcap3_LMM, aaCalibrateSwaption2_LMM, aaVol_Crv_Rcap_BL

LMM calibration functions and caplet volatility bootstrapping function

 

aaCallSnowball_LMM_fs, aaCallSnowball_LMM_LV_fs, aaCallSnowball_LMM_fs_tbl

Snowball valuation functions

 

aaSwaption_dgen, aaSwaption_dgen_cf, aaSwaption2_dgen, aaSwaption2_dgen_cf, aaSwaption_HW, aaSwaption_BK, aaSwaption2_HW, aaSwaption2_BK, aaSwaption_MF

Short-rate tree-based Bermudan swaption valuation functions

 

aaCaplet_HW, aaCaplet_BK, aaCaplet_MF, aaRcap_HW, aaRcap_BK, aaRcap_MF, aaSwaption_eu_HW, aaSwaption_eu_BK, aaSwaption_eu_MF, aaCalibrateRcap2_HW, aaCalibrateRcap2_BK, aaCalibrateRcap2_MF, aaCalibrateSwaption2_HW, aaCalibrateSwaption2_BK, aaCalibrateSwaption2_MF

Short rate calibration and calibration instrument pricing functions

 

References

[1]          Andersen, L. and Andreasen, J. (1998), ‘Volatility Skews and Extensions of the Libor Market Model’, Mathematical Finance, 7, 127-155.

[2]          Brace, A., Gatarek, D., and Musiela, M. (1997), ‘The Market Model of Interest Rate Dynamics’, Mathematical Finance, 7, 127-155.

[3]          Brigo, D. and Mercurio, F. (2001), Interest Rate Models, Theory and Practice, Berlin: Springer.

[4]          Hull, J. (2003), Options, Futures and Other Derivatives, 5th ed., Upper Saddle River: Prentice-Hall.

[5]          Hull, J. and White, A. (2000), ‘Forward Rate Volatilities, Swap Rate Volatilities, and the Implementation of the Libor Market Model’, Journal of Fixed Income, 10 (3), 46-62.

[6]          Jaeckel, P. (2002), Monte Carlo Methods in Finance, West Sussex: Wiley.

[7]          Joshi, M. (2003), The Concepts and Practice of Mathematical Finance, Cambridge: Cambridge University Press.

[8]          Longstaff, F. and Schwartz, E. (2001), ‘Valuing American Options by Simulation: A Simple Least Squares Approach’, The Review of Financial Studies, 14, 113-147.

[9]          Molgedey, L. (2002), ‘Calibration of the deterministic and stochastic volatility Libor Market Model’, Frankfurt MathFinance Workshop 2002.

[10]      Muck, M. (2003) ‘On the Similarity between Displaced Diffusion and Constant Elasticity of Variance Market Models of the Term Structure’, German Finance Association 11th Annual Meeting, Tuebingen, Germany.

[11]      Pedersen, M. (1999), ‘Bermudan Swaptions in the LIBOR Market Model’, SimCorp Financial Research Working Paper.

[12]      Piterbarg, V. (2003), ‘A Practitioner's Guide to Pricing and Hedging Callable Libor Exotics in Forward Libor Models’, Unpublished.

[13]      Rebonato, R. (1999), ‘On the simultaneous calibration of multi-factor log-normal interest-rate models to Black volatilities and to the correlation matrix’, The Journal of Computational Finance, 2, 5-27.

[14]      Rebonato, R. (2002) Modern Pricing of Interest-Rate Derivatives, Princeton: Princeton University Press.

 

 

Disclaimer

 

With respect to this document, FinancialCAD Corporation (“FINCAD”) makes no warranty either express or implied, including, but not limited to, any implied warranty of merchantability or fitness for a particular purpose. In no event shall FINCAD be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of the use of this document or the information contained in it. This document should not be relied on as a substitute for your own independent research or the advice of your professional financial, accounting or other advisors.

 

This information is subject to change without notice. FINCAD assumes no responsibility for any errors in this document or their consequences and reserves the right to make changes to this document without notice.

 

Copyright

 

Copyright © FinancialCAD Corporation 2008. All rights reserved.