Multi-Factor Short Rate Models

Overview

This document describes the FINCAD functions provided for two-factor short rate models. The benefit of using two factor models over one-factor models is that they are able to describe a wider variety of evolutions of the yield curve. This is important for interest rate derivatives whose price depends on the correlations between different interest rates. For more information on two-factor short rate models see Brigo and Mercurio [1], Hull [2], [3] and Rebonato [5]. Functional coverage includes:

· Calibration (using caps/floors and European swaptions)

· Caps/Floors

· European/Bermudan swaptions

· Bermudan CMS/in-arrears swaptions

· CMS/in-arrears swaps/FRN’s

Formulas & Technical Details

Model

FINCAD provides an implementation of the 2 Additive Factor Gaussian (2AFG) short rate model proposed by Brigo and Mercurio [1]. In their model, the instantaneous short rate is :

Equation 1

and the processes for and are described by:

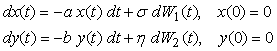
Equations 2 (a) & (b)

where (,) is a 2-D Brownian motion with instantaneous correlation satisfying the following:

Equation 3

It can be shown that another popular 2 factor short rate model proposed by Hull and White is related to the 2AFG model. In the Hull-White 2 factor (HW2F) short rate model, the instantaneous short rate is described by the following equation:

Equation 4

with a mean-reversion process described by:

Equation 5

and instantaneous correlation given by:

Equation 6

Brigo and Mercurio [1] show that by using a suitable change of parameters, the HW2F model can be transformed into the 2AFG model (i.e. transforming ). The 2AFG framework was implemented rather than the HW2F framework because it is easier to work with and analytic formulas for pricing caplets and European swaptions are provided for 2AFG (although it requires root finding and numerically evaluating an integral). However, the functions provided do allow the user to input HW2F model parameters (the HW2F parameters are transformed so they can be used in the 2AFG implementation).

Calibration

The calibration functions for two-factor short rate models are described in the Calibration FINCAD Math Reference document. Note that when calibrating to caplets, the calibration functions may return different fitted parameter values for different initial parameter guesses. This may happen because caplet prices contain information about volatilities of rates but not about correlations between rates. Conversely, swaption prices contain information about both rate volatilities and correlations. In any case, the quality of a calibration can be determined by examining the convergence flag and error statistic that are returned by the calibration function (see the Calibration FINCAD Math Reference document for more information).

Pricing

Functions are provided for pricing Bermudan swaptions and CMS Bermudan swaptions. These are implemented with a 3-D trinomial tree using the tree building procedure presented in Hull and White [3]. Note that the tree may lead to poor results for certain parameter values as reported by Muck and Rudolf [4] and Staley and Wickentowich [6]. This is due to the possibility of negative transition probabilities when constructing the tree. The approach used to handle negative transition probabilities (see [3]) produces the worst results when the correlation parameter approaches +/-1 in the 2AFG model. For more information on this issue, see Refs [1], [2], [3], [4] and [6].

FINCAD Functions

aaCaplet_MF(d_v, d_exp, d_e, d_t, model_type, model_parms, df_crv, intrp, stat)

Calculates fair value of a caplet or floorlet using a multi-factor short rate model.

aaRCap_MF(d_v, rcap2_obj, acc, df_crv, intrp, model_type, model_parms)

Calculates the fair value and the implied forward rate for a table of caplets or floorlets using a multi-factor short rate model.

aaSwaption_eu_MF(d_v, d_e, d_m, princ, cpn, freq, acc, d_rul, swpn, d_exp, hl, df_crv, intrp, model_type, model_parms, stat)

Calculates fair value for a European style swaption using a multi-factor short rate model.

aaSwaption_MF(d_v, d_e, d_m, princ, cpn, freq, acc, d_rul, swpn, d_call, d_call_exp, hl, df_crv, intrp, model_type, model_parms, iter_cpn, freq_flt, mgn, stat)

Calculates fair value for a Bermudan style swaption using a multi-factor short rate model.

aaSwaption_CMS(d_v, d_e, d_m, princ, cpn, freq_fix, acc_fix, d_rul, swpn, d_call, d_call_exp, hl, df_crv, intrp, model_type, model_parms, iter_cpn, freq_flt, acc_flt, mgn, freq_cms, numcf_cms, acc_cms, set_coupon, reset_mktdays, r_rate_obj, stat)

Calculates fair value for a Bermudan style CMS swaption using a multi-factor short rate model. Can also be used to value in-arrears swaptions and CMS/in-arrears swaps.

aaSwaption_CMS_cf(d_v, d_e, d_m, princ, cpn, freq_fix, acc_fix, d_rul, swpn, d_call, d_call_exp, hl, df_crv, intrp, model_type, model_parms, iter_cpn, freq_flt, acc_flt, mgn, freq_cms, numcf_cms, acc_cms, set_coupon, reset_mktdays, r_rate_obj, table_type)

Calculates cashflows and other tables related to a Bermudan style CMS swaption using a multi-factor short rate model. Can also be used to value in-arrears swaptions and CMS/in-arrears swaps.

Description of Inputs

Input Argument	Sample Data	Description
d_v	15-Jan-2000	Valuation (Settlement) Date
d_e	15-Jan-2000	Effective date
d_m	15-Jan-2003	Maturity Date
d_t	15-Jan-2003	Termination Date
d_exp	15-Jan-2001	Expiry Date
princ	1000000	Principal Amount
cpn	0.05	Coupon rate
freq	1 (for annual)	Frequency
acc	4 (for 30/360)	Day Count Convention
d_rul	2 (for next good business day)	Business Day Convention
swpn	1 (for right to pay fixed)	Specify as either a payer or receiver swaption
d_call	20-Jan-2001	First date on which the option can be exercised
d_call_exp	10-Jan-2003	Last date on which the call or put can be exercised
hl	t_26_3	Holiday list
df_crv	t_43_6	Discount Factor Curve
intrp	1 (for linear)	Interpolation Method
model_type	1 (for Hull-White 2 factor)	Short rate model type
model_parms	t_884	Table containing parameters for short rate model
iter_cpn	2	Number of time steps in tree per coupon period
freq_flt	1 (for annual)	Frequency of floating leg payments
mgn	0.005	Margin above or below a floating rate
stat	1	Statistic to be output
freq_fix	1 (for annual)	Frequency of fixed leg payments
acc_fix	4 (for 30/360)	Day Count Convention for fixed leg payments
acc_flt	4 (for 30/360)	Day Count Convention for floating leg payments
freq_cms	1 (for annual)	Frequency of underlying CMS rate
numcf_cms	2	Number of cash flows in underlying CMS rate
acc_cms	4 (for 30/360)	Day Count Convention for underlying CMS rate
set_coupon	1 (for set in-advance)	Setting of floating coupons
reset_mktdays	0	Number of business days prior to the reset date that the rate is fixed
r_rate_obj	t_670	Table of fixed reset rates
table_type	1 ( for a 4 column floating cash flow table)	Output table type selection

Description of Outputs

aaCaplet_MF

Output Statistics	Type	Description
1	Number	caplet/floorlet price
2	Rate	Implied forward rate

aaRcap_MF

Output	Type	Description
rcap_obj	Table_377	Table of rate cap or floor prices and forward rates

aaSwaption_eu_MF and aaSwaption_MF

Output Statistics	Type	Description
1	Number	option price
2	Number	expected time to exercise (in years)
3	Number	probability of exercise
4	Number	fair value of fixed leg with option (no accrued)
5	Number	fair value of fixed leg with option (with accrued)
6	Number	fair value of fixed leg (no accrued)
7	Number	accrued interest
8	Number	fair value of fixed leg (with accrued)

Outputs for aaSwaption_CMS

Output Statistics	Type	Description
1	Number	option price
2	Number	expected time to exercise (in years)
3	Number	probability of exercise
4	Number	fair value of fixed leg with option (no accrued)
5	Number	fair value of fixed leg with option (with accrued)
6	Number	fair value of fixed leg (no accrued)
7	Number	accrued interest
8	Number	fair value of fixed leg (with accrued)
9	Number	fair value of fixed leg from tree (with accrued)
10	Number	fair value of floating leg from tree (with accrued)

Outputs for aaSwaption_CMS_cf

Output	Type	Description
cf_tbl_C	Table_994	Table of cash flows for CMS swaption (and underlying swap)

Examples

Example 1: CMS Bermudan Swaptions

This example shows how to use the aaSwaption_CMS function to price a CMS Bermudan swaption with the 2AFG model assuming the model has been calibrated resulting in the following parameters:

Table 1 – Model Parameters

sigma	a	eta	b	rho
0.015245975	0.598990155	0.00593246	0.08297404	-0.3854344

Also, assume the value date is Feb.13, 2001, the effective date of the swaption is Feb.13, 2004 and the maturity date is Feb.13. 2008. The fixed and floating payments are both annual, the principal amount is 100 and the fixed coupon is 5.3%. The swaption is the right to receive fixed and may be exercised on the effective date of each payment period. The floating reset is a 2 year semi-annual CMS rate with no margin. The CMS rate is set at the beginning of each payment period (set in-advance, zero reset market days). An accrual method of 30/360 and no business day adjustments are used in all the calculations. The following discount factor curve and holiday list are used:

Table 2 – Discount Factor Curve		Table 3 – Holiday List

Grid Date	Discount Factor	Date
13-Feb-2001	1	25-Dec-2001
13-Mar-2001	0.996242	1-Jan-2002
13-May-2001	0.988274	25-Dec-2002
13-Aug-2001	0.976839	1-Jan-2003
13-Nov-2001	0.965947	25-Dec-2004
13-Feb-2002	0.955202	1-Jan-2005
13-Feb-2003	0.913289	25-Dec-2005
13-Feb-2004	0.870454	1-Jan-2006
13-Feb-2005	0.828414	25-Dec-2006
13-Feb-2006	0.786668	1-Jan-2007
13-Feb-2007	0.745072	25-Dec-2007
13-Feb-2008	0.704349	1-Jan-2008
13-Feb-2009	0.664992
13-Feb-2010	0.62784
13-Feb-2011	0.592534
13-Feb-2012	0.557407
13-Feb-2013	0.524275
13-Feb-2014	0.493195
13-Feb-2015	0.463957

Because the swaption is forward starting, we do not have any known resets so the input for the fixed reset table is left empty. Also, we use linear interpolation and 5 time steps per time period in the tree calculation. The inputs to the aaSwaption_CMS function are:

aaSwaption_CMS

Argument	Description	Example Data	Switch
d_v	value (settlement) date	13-Feb-2001
d_e	effective date	13-Feb-2004
d_m	maturity date	13-Feb-2008
princ	principal	100
cpn	coupon	5.3%
freq_fix	frequency of fixed leg	1	annual (Switch_13)
acc_fix	accrual method for fixed leg payments	4	30/360 (ISDA) (Switch_331)
d_rul	business day convention for coupon payments	1	no date adjustment (Switch_116)
swpn	swaption type	1	right to receive fixed (Switch_95)
d_call	first call or put date	13-Feb-2004
d_call_exp	last call or put date	13-Feb-2008
exer_date_type	exercise date type	1	fixed coupon effective dates (Switch_941)
hl	holiday list	Table 3
df_crv	discount factor curve	Table 2
intrp	interpolation method	1	linear (Switch_37)
model_type	model type	2	two additive factor gaussian (Switch_888)
model_parms	model parameters table	Table 1
iter_cpn	number of time steps per time period	5
freq_flt	frequency of floating leg	1	annual (Switch_13)
acc_flt	accrual method for floating leg payments	4	30/360 (ISDA) (Switch_331)
mgn_cms	margin above or below the floating reset (constant maturity yield)	0.0%
freq_cms	frequency of underlying constant maturity yield	2	semi-annual (Switch_13)
numcf_cms	number of cashflows in underlying bond (or Swap)	4
acc_cms	accrual method of underlying constant maturity yield	4	30/360 (ISDA) (Switch_331)
set_coupon	setting of coupons	1	set in advance (Switch_945)
reset_mktdays	number of business days prior to the reset date that the rate (constant maturity yield) is fixed	0
r_rate_obj	fixed reset rates (constant maturity yield)	Empty
stat	statistics	1,…,10

The results from the aaSwaption_CMS function are:

Table 4 – CMS Bermudan Swaption Output

Output Statistics	Description	Value
1	option price	1.38158627
2	expected time of exercise (in years)	5.280425782
3	probability of exercise	0.533042681
4	fair value of fixed leg with option (no accrued)	85.29521464
5	fair value of fixed leg with option (with accrued)	85.29521464
6	fair value of fixed leg (no accrued)	86.67680091
7	accrued interest	0
8	fair value of fixed leg (with accrued)	86.67680091
9	fixed leg from tree (with accrued)	86.67680091
10	float leg from tree (with accrued)	87.14590847

In-arrears Bermudan Swaptions

Note that the aaSwaption_CMS function has a “set_coupon” input which should be set to 1 if the floating reset is set at the beginning of the floating coupon payment period (in-advance) or 2 if it is set at the end (“in-arrears”). Using this input, the aaSwaption_CMS function can be used to price set “in-arrears” swaptions as well. For “in-arrears swaptions” on forward rates, set the number of cashflows in the underlying swap to 1 so the underlying swap rate is now a forward rate (at the frequency specified by the “freq_cms” input).

CMS/In-arrears Swaps/FRNs

The aaSwaption_CMS function also has an output statistic for the floating leg of the underlying swap. This allows the user to price CMS/in-arrears swaps and FRN’s using a two factor short rate model. A cash flow function aaSwaption_CMS_cf is also provided which generates the individual fixed and floating leg cash flows.

Related Functions

Two-factor calibration functions:

aaCalibrateRCap2_MF

aaCalibrateSwaption2_MF

One-factor tree-based Bermudan swaption functions:

One-factor calibration and related functions:

aaCalibrateSwaption2_HW

aaCalibrateSwaption2_BK

CMS/In-arrears functions using Black’s model:

aaFRN_arrears_dgen_cf

aaFRN_arrears_dgen_iv

aaFRN_arrears_dgen_p

aaFRN_arrears_dgen_tables

References

[1] Brigo, Damiano, Mercurio, Fabio, (2001), Interest Rate Models, Theory and Practice, Springer.

[2] Hull, John, (2003), Options, Futures and Other Derivatives: 5th ed., Prentice-Hall.

[3] Hull, John, White, Alan, (Winter 1994), ‘Numerical procedures for implementing term structure models II: Two-factor models’, Journal of Derivatives, 2.

[4] Muck, Matthias, Rudolf, Markus, (February 2002), ‘An extension of the discrete implementation of the Hull-and-White-2-Factor-Model’.

[5] Rebonato, Riccardo, (1998), Interest Rate Option Models: 2nd ed., Wiley.

[6] Staley, Mark, Wicentowich, Cameron, (December 2003), ’Spline Trees: Binomial Lattices for Multi-Factor Processes’.

Disclaimer

With respect to this document, FinancialCAD Corporation (“FINCAD”) makes no warranty either express or implied, including, but not limited to, any implied warranty of merchantability or fitness for a particular purpose. In no event shall FINCAD be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of the use of this document or the information contained in it. This document should not be relied on as a substitute for your own independent research or the advice of your professional financial, accounting or other advisors.

This information is subject to change without notice. FINCAD assumes no responsibility for any errors in this document or their consequences and reserves the right to make changes to this document without notice.