Credit Default Swaps
Overview
A credit default swap is a contract that provides
protection against credit loss on an underlying reference entity as a result of
a specific credit event. A credit
event is usually a default or, possibly, a credit downgrade of
the entity. The reference entity may be a
name, a bond, a loan, a trade receivable or some other type of liability. The buyer of a default swap pays a premium to
the writer or seller in exchange for right to receive a payment should a credit
event occur. In essence, the buyer is
purchasing insurance.
There are two types of conditional payments. One type of payment is a predetermined fixed
cash amount. The other type of payment,
determined at the time of the credit event, is equal to the difference between
the face value and the recovered amount of the reference entity, this payment
is made either at the time of the credit event or at the maturity of the
contract. There are also several
variations of premium payments. The
premium may be paid at inception or may be paid over time as a fixed or
variable amount. A default swap with a
payoff of a fixed amount is known as a binary (cash or
nothing) default swap. A default swap
with its premium paid at inception is also called a default put.
The value of a default swap depends not only on the credit
quality of the underlying reference entity but also on the credit quality of
the writer, also referred to as the counterparty. If the counterparty defaults, the buyer of a
default swap will not receive any payment if a credit event occurs. We also note that the premium payments end if
the counterparty defaults. Hence, the
value of a default swap depends on the probability of counterparty default,
probability of entity default and the correlation between them.
The recovery rate of a reference entity also plays an
important role in default swap valuation. It must be handled carefully. In the case of a bond, its recovery rate can refer
to a recovery rate of its principal only or to a recovery rate of both its
principal and accrued interests. A
recovery rate can also be deterministic or random. However, under the assumption that a recovery
rate is independent of other variables, a random recovery rate can be replaced
by its expected value and hence only deterministic recovery rates need to be
considered. In FINCAD functions all
recovery rates are assumed to be expected recovery rates. If the entity is a bond, different recovery
rates for the bond’s principal and coupon are allowed. Particularly, both cases of principal-only
recovery rates and recovery rates for principals and coupons are handled in the
functions.
The following FINCAD functions value default swaps on a single
entity with no counterparty default risk. The basic assumption in the valuation is that
interest rates, recovery rates and default events are independent. For basket-linked default swaps and default
swaps with counterparty default risk, see the Basket
Default Swaps FINCAD Math Reference document.
Formulas & Technical Details
We consider a typical credit default swap, a swap on a
bond with a maturity greater than or equal to the default swap’s maturity, a
counterparty default probability of 0, periodic premium payments, and the swap
starts at time 
= 0. Its payoff at time 
is:
where:
is the time to
maturity,
is the bond’s
principal,
and 
are the recovery rates
of principal and coupon respectively (typically, 
or 
) and
is the accrued
interest at time on a notional of 1.
Suppose that the default density function of the
bond is 
. Then the present
value of this payoff is:
where:
is the risk-free
discount factor at time .
Let 
be the cumulative risk
neutral default probability of the bond at time 
. Then:
Suppose
the premium rate is 
. If the contract
specifies that accrued premium interest must be paid, then the expected present
value of the premium payments is:
otherwise the present premium value is:
where
is the payment time of
the 
premium coupon (
) and
is the accrued
interest, on a notional of 1, of the 
premium coupon at time
at the rate of
100%.
The fair value of the default swap is simply the present
value of the payoff minus the present value of the premium payments. To get the par default swap spread we can set
the fair value of the default swap to be 0 and solve for the premium rate . The default swap
spread is then:
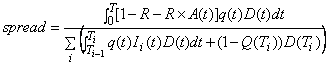
Note that if the premium has accrued interest at
time 0 the denominator in the above equation must be the fair premium minus the
accrued interest.
In a credit derivative contract, an upfront payment might
be required to capture the difference between the deal spread and the
prevailing market spread. When this fee
is taken into account, the default swap spread above changes to
where Premium(1)
denotes the premium payments with the coupon rate equal to 1=100%.
To calculate the integrals in the above formulas
some approximation is necessary. There
are many ways to approximate integrals.
Popular ones are trapezoidal rule and Simpson’s rule and their extended
versions. In FINCAD all these methods
are implemented except for the trapezoidal rule, which has been modified as
follows:
This method is called the “simplified calculation
method” in FINCAD functions, and will produce results comparable to those from
the JPMorgan® model on Bloomberg®.
Note: The differences in CDS value as a result
of different integration methods depend not only on the integration methods
used, but also on the given default probability and risk-free discount factor
curves. For example, if such curves are far away from a linear approximation in
premium payment periods, the CDS values calculated with the simplified
calculation method may be significantly different from those calculated with
other integration methods.
FINCAD Functions
Regular default swaps
Default swaps with a payoff depending on the market value
of the reference entity at the default time.
Type 1
The default swap protects the principal notional amount of
the entity. It is assumed that when the entity
defaults a portion of the notional is recovered. The payoff to the buyer of such a default swap
when the entity defaults is then:
where
is the notional and
is its recovery rate.
If the entity is a bond, this means no accrued
interest is recovered. On the other
hand, if a portion of its accrued interest can be recovered, the payoff to the
buyer of the default swap is:
where
is the bond’s
principal,
is accrued interest per one unit of principal at the default time
and
and 
are the recovery rates
of the bond’s principal and coupon respectively.
The premium can be paid periodically and/or at fixed
time points.
aaCDS_std(d_v,
contra_d, princ_pr, cpn_pr, freq_pr, pr_acc_type, acc, d_rul, front_fee, p_off,
p_off, dp_type, dp_crv, intrp_tb, rate_recover, hl, dfstd, intrp, pos, calc_para,
stat)
Calculates fair
value, payoff and premium values and risk statistics of a credit default swap using
simplified calculation method. Both
IMM and standard date generation methods are allowed.
aaCDS(d_v,
contra_d, cpn_pr, freq_pr, pr_acc_type, acc, d_rul, prem_fix, ref_type, ref_tbl,
p_off, dp_type, dp_crv, intrp_tb, rate_recover, hl, dfstd, intrp, pos, calc_para,
stat)
Calculates fair
value, payoff and premium values and risk statistics of a credit default swap. The default estimation data of the reference
name can be a par CDS spread curve or a default probability curve. Upfront fees
and three types of date generation methods are allowed.
Remark: If one sets cpn_pr = 0 and defines pr_fix as a
single element array with the value of an upfront fee (% notional), one can use
function aaCDS
to value a default put.
aaCDS_is(d_v,contra_d,cpn_pr,freq_pr,pr_acc_type,acc,d_rul,pr_fix,ref_type,ref_tbl,p_off,cds_p,dp_type,dp_crv,intrp_tb,rate_recover,hl,dfstd,intrp,calc_type)
Calculates the implied spread of a credit default swap
given a price.
aaCDS_if(d_v,
contra_d, cds_sprd, cpn_pr, freq_pr, pr_acc_type, acc, d_rul, prem_fix,
ref_type, ref_tbl, p_off, dp_type, dp_crv, intrp_tb, rate_recover, hl, dfstd,
intrp, pos, calc_para)
Calculates the implied upfront percentage payment of a
credit default swap given a par CDS spread.
aaCDS_cf(d_v,contra_d,cpn_pr,freq_pr,pr_acc_type,acc,d_rul,pr_fix,npa,p_off,dp_type,dp_crv,intrp_tb,rate_recover,hl,dfstd,intrp,pos,calc_para,table_type)
Calculates the premium cash flows of a credit default swap
and the expected payoffs at the premium leg payment dates.
Type 2
The reference entity is a free-style bond (a custom
structure, such as a loan book) with separate coupon and fixed payment
structures and the default swap protects the fixed payments. It is assumed that when the bond defaults a
portion of both its principal and its accrued interests can be recovered. The payoff to the buyer of the default swap
when the bond defaults is then the sum of:
where the
’s are the bond’s outstanding fixed payments, minus the sum
of:
where the
’s are the accrued interests at the default time. The premium of the default swap can be paid
periodically and/or at fixed time points.
aaCredit_DSWap_fs_sep(d_v,
contra_d, princ_pr, cpn_pr, freq_pr, pr_acc_type, acc, d_rul, prem_fix_tbl, loancpn,
loanfixed_tbl, acc_fs, payoff_type, prob_crv, intrp_prob, rate_recover, hl, df_crv_std,
intrp, position, calc_type, stat)
Calculates the fair value of the default swap, the fair
values of the payoff and premium legs and several other statistics.
Type 3
The reference entity is a free-style bond (a custom
structure, such as a loan book) with a mixed coupon and principal structure and
the premium payment schedule has a customer structure. It is assumed that when the bond defaults a
portion of both its principal and accrued interest can be recovered. The payoff to the buyer of the default swap
when the bond defaults is the sum of:
where
is principal of the coupon and
is its accrued
interest at the default time per one unit of principal,
is the recovery rate
for both principal and accrued interest.
The premium schedule can be customized, in the form of
coupon and/or lump sums.
aaCredit_DSwap_fs(d_v,
d_t, acc_time, prem_tbl, prem_fix_tbl, probordensity, prob_crv, rate_recover, payoff_type,
loan_tbl, yield_riskfree)
Given a risk-free yield, calculates the fair value of a
free-style bond default swap with custom-structured premium payments.
aaCredit_DPayoff_fs(d_v,
d_t, acc_time, probordensity, prob_crv, rate_recover, payoff_type, loan_tbl, yield_riskfree)
Given a risk-free yield, calculates the fair value of the
payoff leg.
aaCredit_DPremium_fs(d_v,
d_t, acc_time, probordensity, prob_crv, prem_tbl, prem_fix_tbl, yield_riskfree)
Given a risk-free yield, calculates the fair value of the
premium of a free-style bond default swap with custom-structured premium
payments.
Note that there are three other corresponding
functions with the additional suffix _crv.
These functions take in a discount factor curve while the ones above
take in a yield.
Binary (digital) default swaps
Default swaps that pay a fixed amount of cash if the
reference entities default.
For a binary default swap the buyer receives a fixed
amount of cash when a credit event occurs. Binary default swaps are much simpler than
regular default swaps since their payoffs depend on the default probability
curve only, and not on the recovery rate or the structure of the underlying entity. The following functions value binary default
swaps:
aaCDS_bin(d_v,
contra_d, cpn_pr, freq_pr, pr_acc_type, acc, d_rul, prem_fix, p_off, cash_rate,
dp_type, dp_crv, intrp_tb, rate_recover, hl, dfstd, intrp, pos, calc_type, stat)
Calculates fair value, payoff and premium values and risk
statistics of a binary credit default swap. The default estimation data of the reference
name can be a par CDS spread curve or a default probability curve.
For a CDS with a custom structured premium payment, use:
aaCredit_DSwap_bin_fs(d_v,
d_t, acc_time, payoff_amt, probordensity, prob_crv, payoff_type, prem_tbl,
prem_fix_tbl, yield_riskfree)
Calculates the fair value of a binary default swap on a
loan.
aaCredit_DSwap_bin_fs_crv(d_v,
d_t, acc_time, payoff_amt, probordensity, prob_crv, payoff_type, prem_tbl,
prem_fix_tbl, df_crv_std, intrp)
Calculates fair value, payoff and premium values and other
statistics of a binary credit default swap with custom
structured premium payments.
Description of Inputs
aaCredit*
|
Input Argument |
Description |
|
d_v |
Valuation date |
|
d_e |
Effective date of a default swap |
|
d_f_prem |
(Odd) first premium coupon date after effective date |
|
d_l_prem |
(Odd) last premium
coupon date before maturity date |
|
contra_d |
A table of default swap date(s).It can be a 1-, 2-, 3-, or
4-entry table. The 4 entries hold in
sequence the maturity date, effective date, first coupon date and next to
last coupon date for premium payments. Only one entry, the maturity date, is
required. If an entry is not
available, it can be set to be 0 to be ignored. |
|
npa |
Notional principal amount |
|
d_t |
Maturity date of a default swap |
|
princ_m |
Principal amount |
|
princ_pr |
Premium notional amount |
|
cpn_pr |
Premium payment rate |
|
freq_pr |
Premium payment frequency - a switch |
|
pr_acc_type |
Type of premium accrued interest payments - a switch: 1 = pay accrued interest of premium at default, 2 = pay no accrued interest of premium at default |
|
acc |
Accrual method of premium |
|
d_rul |
Business date convention for premium payment - a switch |
|
payoff_type |
Type of settlement time - a switch: 1 = payment to the CDS buyer is made at the time of
default, 2 = payment to the CDS buyer is made at the default swap's
termination. |
|
prob_crv |
A default probability curve. It can be a two or three column table. The first column can be time in years
(>=0 and <1000 ), or dates (>=1000) and the second default
probability values. Time and date must
be increasing. Probability must be
non-decreasing and between 0 and 1. If
the first column is time in years, the time accrual method (default = 30/360)
can be put in the first row of the third column. For a date based curve, the first value of
the second column must be 0 and the first date must be the valuation date. Excel users may pass term strings to
represent time intervals. Term strings
must be in the format kB, kD, kW, kM, or kY where k is an integer and D, W, M
and Y stands for calendar day, week, month and year respectively, e.g., 3M =
3 months. |
|
intrp_prob |
Interpolation method of a probability curve - a switch: 1 = linear, 2 = exponential. For both interpolation methods, if curve extension is
needed, the exponential extrapolation method is always used for curve
extension. |
|
rate_recover |
In functions dealing with CDS with regular premium
payments, this is an expected recovery rate table. It can be of 4 types: 1. a
one-entry table which has the recovery rate for both principal and coupon. 2. a
two-entry table which has the recovery rates for principal (the first entry)
and coupon (the second entry) respectively. 3. a
three-column table which is a time-dependent recovery rate table for
principal and coupon. The first column
has time in years. 4. a
four-column table which is similar to a three-column table except that the
entry in the first row of the fourth column holds the delay time (in years)
for the recovery payment. The default
recovery delay time is 0 which represents the assumption that recovery is
made immediately at default. In
functions valuing default swaps with custom-structured premium payments, it
is a single value of recovery rate, which is a recovery rate for both coupon
and principal. |
|
acc_time |
Time accrual method - a switch |
|
prem_fix_tbl |
Fixed premium table. It is a two-column table: (date, premium). Premium paid prior to (not equal to) the
value date or after (not equal to) the maturity date is ignored. This table can hold any fixed premium
payments additional to the premium coupons. |
|
bond_data_9 |
A 9-entry bond data table (principal, maturity, dated
date, first coupon date, next to last coupon date, coupon, frequency, accrual
method, business day convention). See aaBond3
for details. |
|
hl |
A holiday list |
|
df_crv_std |
Risk-free discounting factor curve or a risk-free yield. If it is a risk-free yield table, it can be
a one entry table of a yield value (annual, actual/365), or a two entry table
of yield and compounding frequency or a three entry table of yield, a
compounding frequency and a day count convention. |
|
intrp |
Interpolation method of the discount factor curve – a switch |
|
position |
Trading position - a switch: 1 = pay premium, 2 = receive premium. |
|
calc_type |
Type of calculation method - a switch. Generally, it has 4 values. They represent
different integration methods for calculating values of premiums and payoffs.
There are four selections: 1 = simplified calculation method, 2 = extended trapezoidal, 3 = Simpson's rule, 4 = extended Simpson's rule. In aaCredit_DS_SPV01, only the first method is
implemented. |
|
stat |
Statistics: any subset of {1,2,…,11} |
|
spread_tbl |
Par credit default spread table. It is a five-column table: (effective date of a default swap,
terminating date, par spread, type of accrued interest payment, recovery
rate). The terminating date must be in
increasing order. The type of accrued
interest payment takes two values: 1 = pay accrued interest of premium upon default, 2 = pay no accrued interest of premium up on default. |
|
loanCpn |
The coupon table of a free-style bond. It has four columns: effective date,
maturity date, principal, coupon rate. Interest payments and accrued interests that
do not fall within the interval (d_v, d_t) are ignored. |
|
loanfixed_tbl |
The fixed payment table of a free-style bond. It has two columns: date, amount. |
|
acc_fs |
Accrual method(s) of a free-style bond. If it has only one entry, both future coupon
payments and accrued interests have the same accrual method; otherwise they
are the first and second entries of the table, respectively. |
|
yield_riskfree |
Risk free yield to maturity. |
|
payoff_amt |
Payoff amount for a binary default swap |
|
cash_rate |
Payoff amount per one unit of notional for a binary
default swap. |
|
prem_tbl |
Premium payment table for user-defined premium payments. It is a four-column table (effective date,
terminating date, notional, premium rate). Premium payments made prior to the valuation
date are ignored. An accrued premium
payment must be paid and its present value is included in the fair value. |
|
loan_tbl |
Loan table. A four
column table (effective date, terminating date, principal, rate). If terminating date<=d_v or effective
date>=d_t, then the loan is ignored. |
|
probordensity |
Probability or density - a switch: 1 = probability, 2 = density |
|
table_type |
Table type of premium cash flows, a switch. See the section Description
of Outputs for details. |
aaCDS*
|
Input Argument |
Description |
|
d_v |
value (settlement) date |
|
d_e |
effective date |
|
d_t |
terminating date |
|
d_f_cpn |
date of first coupon after dated date |
|
d_l_cpn |
date of last coupon prior to maturity date |
|
contra_d |
Contra_d is a table of default swap date(s). It can have 2 to 7entries. The first four entries hold in sequence the
terminating date, effective date, odd first coupon date and next-to-last
coupon date for premium payments. The last three entries hold switch values
in sequence the effective date adjustment, terminating date adjustment and
date generation method for premium payments. Only the terminating date and
effective date are required. The third entry and fourth entry will default to
0 and the last three entries will default to 1 (adjust effective date, adjust
terminating date, backward date generation). Note that for most credit default
swaps in the market, the effective date and maturity date are not adjusted
and the premium cash flow dates are IMM dates. For this case, simply set both the effective
date and maturity date adjustment methods (the 5th and 6th
entries in the table) to 2 (no adjustment) and the date generation method
(the 7th entry in the table) to 3 (IMM date generation method). |
|
princ_pr |
premium notional principal |
|
cpn_pr |
premium coupon rate |
|
freq_pr |
premium payment frequency |
|
pr_acc_type |
type of premium accrued interest payment – a switch: 1 = pay accrued interest upon default, 2 = pay no accrued interest upon default |
|
acc |
accrual method |
|
d_rul |
business day convention |
|
pr_fix |
An upfront fee and fixed premium table. It can be a
single-element array or a two-column table. If it is a single element array,
it is the upfront fee (the upfront payment per one unit of notional). If it
is a two column table, it can store an upfront fee and fixed premium
payments. If the element in the first row and first column, pr_fix(1,1),
<= 1000, it is an upfront fee. Otherwise, the first row has a fixed
premium payment: (date, premium amount). All other rows always have fixed
premiums. Note that an upfront fee must be >=0 and <=1 and premium
payment dates must be increasing. |
|
ref_type |
type of reference – a switch: 1 = name (notional), 2 = bond (a level coupon bond) |
|
ref_tbl |
Reference data table. If the reference type ref_type = 1, it is a one entry
(notional) table. If the reference type ref_type = 2, it is the details of a
bond. It is a 9-column table. These columns are (principal, maturity,
dated date, first coupon date, next-to-last coupon date, coupon, frequency,
accrual method, business day convention). See aaBond3 for
their definitions. |
|
p_off |
payoff type – a switch: 1 = pay at default, 2 = pay at maturity |
|
cash_rate |
payoff rate (cash payment per one unit of notional
principal) |
|
dp_type |
default curve type – a switch: 1 = par CDS spread curve, 2 = default probability curve |
|
dp_crv |
A default curve, either a default probability or a CDS
spread curve, can be time-based (the first column >0 and <1000) or
date-based (the first column >=1000). If it is a default probability curve or a
time-based CDS spread curve, the first column has time (in years) or dates. If it is a date-based CDS spread curve, the
first two columns have the effective and terminating dates of the CDS
spreads. The next m columns have
default probabilities/CDS spreads, where m is the number of reference
entities. These columns must be
ordered in the same way as in the reference data table. Times and dates (the terminating dates for a
CDS spread curve) must be increasing. For
a time-based curve, the time-accrual method can be put in the third entry of
the table intrp_tb (see note 429). Probabilities must be nonnegative, <=1
and nondecreasing. CDS spreads must be nonnegative. For a date-based default probability curve,
the probabilities in the first row must be 0 and the first date must be the
valuation date if there is one. Excel
users may pass term strings to represent time intervals. Term strings must be in the format kB, kD,
kW, kM, or kY where k is an integer and D, W, M and Y stands for calendar
day, week, month and year respectively, e.g., 3M = 3 months. |
|
intrp_tb |
A default curve parameter table. The array intrp_tb can
have one to six entries. The first entry has the default probability curve
interpolation method. The second entry has the default probability curve
bootstrapping method (see switch sw_1040 in aaCredit_dfltprob_DSSpred2).
It is used only if the default curve type is "par CDS spread curve"
( dp_type =1). If this entry is missing and dp_type=1, the bootstrapping
method will be set to method 1 (assuming constant density). The third entry
stores the time accrual (day counting) method if the default curve is
time-based. If this entry is missing and the default curve is time-based, the
time accrual method will be set to 30/360. If the default curve is not time
based, this entry will be ignored. The fourth to sixth entries store the
effective and terminating date adjustment methods and the date generation
method of CDSs in a CDS curve, respectively. These entries are used only when
dp_type = 1. Their default values are 1. |
|
dp_para |
The array dp_para is a default curve parameter table, it can
have one to four entries. The first
entry has the default probability curve interpolation method. The second entry has the default probability
curve bootstrapping method (see switch sw_1207 in aaCredit_dfltprob_DSSprd_std).
It is used only if the default curve
type is "par CDS spread curve" ( dp_type =1). If this entry is
missing and dp_type=1, the bootstrapping method will be set to method 1 (assume
constant default density). The third
entry stores the time accrual (day counting) method if the default curve
dp_bskt is time-based. If this entry
is missing and dp_bskt is time-based, the time accrual method will be set to
30/360. If the default curve is not
time based, this entry will be ignored. The fourth entry indicates if the maturity
dates in the CDS spread table are IMM dates or standard dates. If they are IMM dates and the default curve
type is "par CDS spread curve" ( dp_type =1), all the CDS
maturities in the curve will be adjusted to IMM maturities in building a
default probability curve. If this
entry is missing or the default curve type is "default probability
curve", the standard maturities are used. |
|
rate_recover |
The recovery rate table. It can be of 3 types: 1.
a one-entry table of a recovery rate; 2. a
two-column table (time in years, recovery rate). 3. a
three-column table (time in years, principal recovery rate, coupon recovery
rate). The third type is only for the case that ref_type=2. If ref_type=2 and the recovery rate table is
type 1 or 2, then the principal and coupon have the same recovery rate. For aaCDS_std, only the first two types are
allowed. For binary CDS functions (aaCDS_bin*), it
is a single number of the recovery rate. |
|
recs |
The recovery rate table. It is an array of recovery rates.
It is used only if the input default
curve is a par CDS spread curve (dp_type=1). |
|
hl |
holiday list |
|
df_crv_std, dfstd |
The discount factor curve may be input as a 2-column,
multi-row table (col 1 = date, col 2 = discount factor), or as a single cell
containing a rate. If input as a
single rate, there are three format choices: 1.
a rate (1 row, 1 column); or 2. a
rate and a rate quotation basis (1 row, 2 columns); or 3. a
rate, a rate quotation basis, and an accrual method (1 row, 3 columns). If the basis or accrual are not provided, they are assumed
to be annual, actual/365. A 2-column
flat-rate discount factor curve is constructed internally using the rate,
basis, and accrual method. The last
date in the discount factor curve >= last "date" in the default
curve and the terminating date of the swap. |
|
intrp |
interpolation method |
|
pos |
trade position – a switch: 1 = long, 2 = short |
|
calc_para |
The table calc_para can have 1 or 2 entries. The first entry is a calculation method used
in CDS valuation (see switch sw_624 in the function aaCDS). The optional second entry is the number of
basis points used in DVOX calculation; it is defaulted to 1 when missing. Note that if the absolute value of the
second entry is large the function can fail. |
|
table_type |
output type – a switch: see the output description below
for details |
|
cds_p |
the price of a CDS. |
|
cds_sprd |
the par spread of a CDS |
Note: In most
functions of aaCDS_*,
the table, pr_fix, is taken as an optional input
generally that combines both upfront fee and fixed premium payments except for aaCDS_if. Since this function calculates the implied
upfront percentage payment as output, the table pr_fix
would only contain the fixed premium payments.
See its function reference
for more details.
Description of Outputs
For the functions that calculate fair value and risk
statistics, the outputs are
|
Output Statistic |
Description |
|
1 |
fair value: fair value of a default swap (= payoff – premium
) |
|
2 |
payoff: fair value of the insurance (i.e. loss due to
default) |
|
3 |
Premium: fair value of the periodic premium payments |
|
4 |
accrued interest of premium |
|
5 |
fair value minus accrued interest |
|
6 |
par spread: premium rate that makes the default swap have a
fair value - accrued interest a value
of 0. |
|
7 |
BPV on risk-free curve: the change in fair value per one
basis up shift of the risk-free discount factor curve |
|
8 |
number of days that premium accrues |
|
9 |
next premium payment date |
|
10 |
Previous premium payment date |
|
11 |
remaining coupons: number of remaining coupons of the
premium payments up to the maturity of the default swap |
|
12 |
DVOX of par CDS spread curve: the change in fair value per
X basis points up shift of the par CDS spread curve of the reference entity. |
|
13 |
rho of recovery rate: the change in fair value per 1%
increase of the recovery rate of the reference entity. |
|
14 |
theta: the change in fair value per one day increase of
valuation date |
For the cash flow function aaCDS_cf,
there are six types of output tables.
|
Output Table Type |
Description |
|
1 |
a 6-column present value cash flow table (date, present
value of premium interest, present value of fixed premium, total present
value of premiums, present value of payoff, total present values) |
|
2 |
a 5-column no-default premium cash flow table (date,
interest, fixed premium, total cash flow, accrued interest) |
|
3 |
a 5-column premium interest table (date, no-default
interest, accrued interest, expected interest, present value of interest) |
|
4 |
a 13-column extended premium cash flow table (date,
no-default interest, no-default fixed premium, total no-default cash flow,
accrued interest, expected interest, expected fixed premium, total expected
premium, present value of interest, present value of fixed premium, total present
value, risk-free discount factor,
cumulative default probability). |
|
5 |
a 6-column expected payoff cash flow table (date, expected
cash flow, present value, absolute default probability, loss given default, risk-free
discount factor) |
|
6 |
a 2-column default probability curve (time, default
probability) |
Remark: In the above table type 5 an absolute
default probability at a time period is the probability that the reference
entity defaults at this time period. In more detail, if the cumulative default
probabilities at the end points of a certain time period are 
, then the absolute default probability is 
For the implied upfront payment function aaCDS_if,
the output is the implied upfront percentage payment.
Examples
Examples are given for a default swap on a bond, a default
swap on a name and a default swap on user-defined loans and receivables.
Example 1 A default swap on a bond
Suppose Company A owns a bond issued by Company XYZ. Company A has concerns that Company XYZ may
default on its bond payments. To insure
against possible losses, Company A purchases a credit default swap from Bank B. The swap started on Dec. 1, 2004 and will
mature on Nov. 1, 2008. Company A pays a
2% premium semi-annually. In return, if Company
XYZ defaults at any time during the life of the swap, Bank B will pay Company A
the difference between the bond principal and whatever is recovered. The bond has a principal of $1,000,000 and
will mature on Dec. 1, 2010. The coupon
is 10% and is paid semiannually. Suppose
today’s date is Dec. 1, 2005, the day count convention for the swap is
actual/360 and calendar dates are used for date counting. The premium payment dates are cycle dates from
the maturity dates and all dates are (non-adjusted) calendar dates. Further,
suppose that the expected recovery rate of the bond in the event of a default
is 40%, the projected default probabilities are as given in the following
table:
Projected Default Probabilities
|
Term (years) |
Probability |
|
1 |
0.022031639 |
|
2 |
0.046242249 |
|
3 |
0.072660268 |
|
4 |
0.101233086 |
|
5 |
0.131884986 |
where the time is calculated with the time accrual (day counting) method 30/360. The
risk-free discount factor curve is given as follows:
Discount Factor Curve – Risk Free
|
grid date |
discount factor |
|
1-Dec-2005 |
1 |
|
1-Jun-2006 |
0.971285862 |
|
1-Dec-2006 |
0.943396226 |
|
1-Dec-2007 |
0.88999644 |
|
1-Dec-2008 |
0.839619283 |
|
1-Dec-2010 |
0.747258173 |
|
1-Dec-2015 |
0.558394777 |
|
1-Dec-2020 |
0.417265061 |
Bank B has been rated AAA by Moody’s for the last
20 years and is financially sound. It is
unlikely it will fail to meet its obligation if Company XYZ defaults and thus
the counterparty risk of the default swap can be ignored.
To value the default swap we consider two cases:
Case 1
The recovery rate is the recovery rate of the bond’s
principal only. Calling function aaCDS(),
using the simplified calculation method, we obtain the following results.
aaCDS
|
Argument |
Description |
Example Data |
Switch |
|
d_v |
value (settlement) date |
1-Dec-2005 |
|
|
contra_d |
CDS contract dates |
see below |
|
|
cpn_pr |
premium coupon rate |
2.000% |
|
|
freq_pr |
premium payment frequency |
2 |
semi-annual |
|
pr_acc_type |
type of premium accrued interest payment |
1 |
pay accrued interest upon default |
|
acc |
accrual method |
2 |
actual/360 |
|
d_rul |
business day convention |
1 |
no adjustment |
|
pr_fix |
upfront fee and fixed premium payment table |
0 |
|
|
ref_type |
type of reference |
2 |
bond (a level coupon bond) |
|
ref_tbl |
reference table |
see below |
|
|
p_off |
payoff type |
1 |
pay at default |
|
dp_type |
default curve type |
2 |
default probability curve |
|
dp_crv |
default curve |
see above |
|
|
intrp_tb |
default curve parameter table |
see below |
|
|
rate_recover |
recovery rate table |
see below |
|
|
hl |
holiday list |
0 |
|
|
dfstd |
discount factor curve |
see above |
|
|
intrp |
interpolation method |
1 |
linear |
|
pos |
trade position` |
1 |
buy protection |
|
calc_para |
calculation parameters |
see below |
|
|
stat |
stat list |
1…14 |
|
CDS contract dates (contra_d)
|
terminating date |
effective date |
|
1-Nov-2008 |
1-Dec-2004 |
Reference table (ref_tbl) is the following bond data table
|
principal |
maturity |
odd dates |
coupon |
frequency |
accrual |
day convention |
||
|
1000000 |
1-Dec-2010 |
0 |
0 |
0 |
10% |
2 |
14 |
1 |
Default curve parameter table (intrp_tb)
|
interpolation of default probability curve |
bootstrapping method |
accrual method of time-based default curve |
|
1 |
1 |
4 |
Recovery rate table (rate_recover)
|
time in years |
principal recovery rate |
coupon recovery rate |
|
3 |
0.4 |
0 |
The calculation parameters (calc_para)
|
calculation method |
Basis point (bump size for DVOX) |
|
1 |
1 |
Results
|
Statistics |
Description |
Value |
|
1 |
fair value |
-15333.79763 |
|
2 |
value of payoff |
38224.77441 |
|
3 |
value of premium |
-53558.57204 |
|
4 |
accrued interest of premium |
-1666.666667 |
|
5 |
fair value minus accrued interest |
-13667.13096 |
|
6 |
par spread |
0.014732461 |
|
7 |
basis point value of risk-free curve |
1.942917715 |
|
8 |
number of days that premium accrues |
30 |
|
9 |
next cash flow date |
38838 |
|
10 |
previous cash flow date |
38657 |
|
11 |
number of remaining cash flows |
6 |
|
12 |
DVOX of par CDS spread curve |
-361.4087799 |
|
13 |
rho of recovery rate |
-652.6110451 |
|
14 |
theta |
-47.63272315 |
Case 2
The recovery rate is the recovery rate of both the bond’s
principal and accrued interest. Change the above recovery rate table to
Recovery rate table (rate_recover)
|
time in years |
principal recovery rate |
coupon recovery rate |
|
3 |
0.4 |
0.4 |
Call function aaCDS() to get the
following results:
aaCDS
|
Argument |
Description |
Example Data |
Switch |
|
d_v |
value (settlement) date |
1-Dec-2005 |
|
|
contra_d |
CDS contract dates |
see above |
|
|
cpn_pr |
premium coupon rate |
2.000% |
|
|
freq_pr |
premium payment frequency |
2 |
semi-annual |
|
pr_acc_type |
type of premium accrued interest payment |
1 |
pay accrued interest upon default |
|
acc |
accrual method |
1 |
actual/365 (fixed) |
|
d_rul |
business day convention |
1 |
no adjustment |
|
pr_fix |
upfront fee and fixed premium payment table |
0 |
|
|
ref_type |
type of reference |
2 |
bond (a level coupon bond) |
|
ref_tbl |
reference table |
see above |
|
|
p_off |
payoff type |
1 |
pay at default |
|
dp_type |
default curve type |
2 |
default probability curve |
|
dp_crv |
default curve |
see above |
|
|
intrp_tb |
default curve parameter table |
see below |
|
|
rate_recover |
recovery rate table |
see above for Case 2 |
|
|
hl |
holiday list |
0 |
|
|
dfstd |
discount factor curve |
see above |
|
|
intrp |
interpolation method |
1 |
linear |
|
pos |
trade position` |
1 |
buy protection |
|
calc_para |
calculation parameters |
see above |
|
|
stat |
stat list |
1…14 |
|
Results
|
Statistics |
Description |
Value |
|
1 |
fair value |
-15955.1 |
|
2 |
value of payoff |
37603.52 |
|
3 |
value of premium |
-53558.6 |
|
4 |
accrued interest of premium |
-1666.67 |
|
5 |
fair value minus accrued interest |
-14288.4 |
|
6 |
par spread |
0.014493 |
|
7 |
basis point value of risk-free curve |
2.043153 |
|
8 |
number of days that premium accrues |
30 |
|
9 |
next cash flow date |
38838 |
|
10 |
previous cash flow date |
38657 |
|
11 |
number of remaining cash flows |
6 |
|
12 |
DVOX of par CDS spread curve |
-355.631 |
|
13 |
rho of recovery rate |
-652.611 |
|
14 |
theta |
-46.4365 |
Example 2 A credit default swap(CDS)
on a name with its cash flow dates IMM dates
Suppose in Example 1 the underlying entity is a name with
a notional of 1,000,000. The default probability
curve of the reference entity is unknown but its CDS spread curve is given as
follows:
Default curve (dp_crv)
|
term |
CDS spread |
|
6m |
0.05 |
|
1y |
0.055 |
|
2y |
0.06 |
|
3y |
0.065 |
|
5y |
0.07 |
Moreover, the premium cash flow dates are IMM
dates and are adjusted to the next business dates except for the effective and
maturity dates which are not adjusted. The cash flow dates of the CDSs in the
CDS spread curve follow the same convention. Since the reference entity is not
a bond, the bond table can be replaced with a single element array of the
notional and the recovery rate table can be replaced with a single element
array of the recovery rate. Call aaCDS, ignoring
holidays for simplicity, to get the following results.
aaCDS
|
Argument |
Description |
Example Data |
Switch |
|
d_v |
value (settlement) date |
1-Dec-2005 |
|
|
contra_d |
CDS contract dates |
see below |
|
|
cpn_pr |
premium coupon rate |
2.000% |
|
|
freq_pr |
premium payment frequency |
2 |
semi-annual |
|
pr_acc_type |
type of premium accrued interest payment |
1 |
pay accrued interest upon default |
|
acc |
accrual method |
2 |
actual/360 |
|
d_rul |
business day convention |
2 |
next business date |
|
pr_fix |
fixed premium payment table |
see above |
|
|
ref_type |
type of reference |
1 |
name (notional) |
|
ref_tbl |
reference table |
1000000 |
|
|
p_off |
payoff type |
1 |
pay at default |
|
dp_type |
default curve type |
1 |
default probability curve |
|
dp_crv |
default curve |
see above |
|
|
intrp_tb |
default curve parameter table |
see above |
|
|
rate_recover |
recovery rate table |
0.4 |
|
|
hl |
holiday list |
0 |
|
|
dfstd |
discount factor curve |
see above |
|
|
intrp |
interpolation method |
1 |
linear |
|
pos |
trade position` |
1 |
buy protection |
|
calc_para |
calculation parameters |
see above |
|
|
stat |
stat list |
1…14 |
|
CDS contract dates (contra_d)
|
Terminating date |
Effective date |
First coupon date |
Next to last coupon date |
Effective date adjustment |
Terminating date adjustment |
Date generation method |
|
20-Dec-08 |
1-Dec-04 |
0 |
0 |
2 |
2 |
3 |
|
|
|
|
|
switch: do not adjust effective date |
switch: do not adjust terminating date |
switch: IMM |
Results
|
Statistics |
Description |
Value |
|
1 |
fair value |
99626.4471 |
|
2 |
value of payoff |
157025.912 |
|
3 |
value of premium |
-57399.464 |
|
4 |
accrued interest of premium |
-9111.1111 |
|
5 |
fair value minus accrued interest |
108737.558 |
|
6 |
par spread |
0.06503676 |
|
7 |
basis point value of risk-free curve |
-17.118741 |
|
8 |
number of days that premium accrues |
164 |
|
9 |
next cash flow date |
20-Dec-05 |
|
10 |
previous cash flow date |
20-Jun-05 |
|
11 |
number of remaining cash flows |
7 |
|
12 |
DVOX of par CDS spread curve |
215.866623 |
|
13 |
rho of recovery rate |
-261.90688 |
|
14 |
theta |
-135.32165 |
Remark: Sometimes, the CDS in this example is called a
CDS on a CDS since the default curve is a CDS spread curve.
To calculate the premium cash flows of the CDS call the
function aaCDS_prem_cf. This function outputs five types of cash flow
tables. Since there are no fixed premiums in the CDS, table type 4 will give
the relevant information about the cash flows.
To expose the premium cash flows and the expected payoffs
at the premium payment dates, one can call the function aaCDS_cf.
The following are the results of the function call
aaCDS_cf
|
Argument |
Description |
Example Data |
Switch |
|
d_v |
value (settlement) date |
1-Dec-2005 |
|
|
contra_d |
CDS contract dates |
see above |
|
|
npa |
notional |
1000000 |
|
|
cpn_pr |
premium coupon rate |
2.00% |
|
|
freq_pr |
premium payment frequency |
2 |
semi-annual |
|
pr_acc_type |
type of premium accrued interest payment |
1 |
pay accrued interest upon default |
|
acc |
accrual method |
2 |
actual/360 |
|
d_rul |
business day convention |
2 |
no adjustment |
|
pr_fix |
fixed premium payment table |
0 |
|
|
p_off |
payoff type |
1 |
pay at default |
|
dp_type |
default curve type |
1 |
cds spread curve |
|
dp_crv |
default curve |
see above |
|
|
intrp_tb |
default curve parameter table |
see above |
|
|
rate_recover |
recovery rate table |
0.4 |
|
|
hl |
holiday list |
0 |
|
|
dfstd |
discount factor curve |
see above |
|
|
intrp |
interpolation method |
1 |
linear |
|
pos |
trade position |
1 |
buy protection |
|
calc_para |
calculation parameters |
1 |
simplified calculation method |
|
stat |
stat list |
1…14 |
|
Results: present
value CDS cash flow table
|
Date |
Premium interest |
Fixed premium |
Total premium |
Payoff |
Total |
|
20-Dec-05 |
-10133.93 |
-0 |
-10133.92896 |
2571.31065 |
-7562.618 |
|
20-Jun-06 |
-9547.835 |
-0 |
-9547.834781 |
23923.6003 |
14375.77 |
|
20-Dec-06 |
-8898.318 |
-0 |
-8898.317735 |
27119.8649 |
18221.55 |
|
20-Jun-07 |
-8155.741 |
-0 |
-8155.740637 |
26275.5802 |
18119.84 |
|
20-Dec-07 |
-7528.363 |
-0 |
-7528.362711 |
25650.8004 |
18122.44 |
|
20-Jun-08 |
-6882.217 |
-0 |
-6882.216674 |
26120.7299 |
19238.51 |
|
20-Dec-08 |
-6253.063 |
-0 |
-6253.062978 |
25364.0254 |
19110.96 |
It is easy to check that the sums of the columns
Premium interest, Payoff and Total match, respectively, those of the outputs of
the function aaCDS
above.
Example 3 CDS spread given a price
Suppose in Example 3 the quoted (clean) price of the CDS
is 9500. To calculate the implied spread that values the CDS to this price,
call the function aaCDS_is with the relevant inputs in Example 2 and the price
parameter cds_p = 9500. The output is 2.569%. One can easily check that if
setting cds_p = 108737.558 (fair value
– accrued interest) of the fifth output of Example 2, the implied spread = 2%,
which is exactly the input premium rate.
Example 4 Valuation of a credit default
swap with an upfront fee
Suppose in Example 2 the contract has an upfront fee of
0.2% and the premium is paid quarterly. To
value the CDS we can call function aaCDS or function aaCDS_std.
The following are the results of the function call to aaCDS_std:
aaCDS_std
|
Argument |
Description |
Example Data |
Switch |
|
d_v |
value (settlement) date |
1-Dec-2005 |
|
|
contra_d |
CDS contract dates |
see below |
|
|
npa |
notional |
1000000 |
|
|
cpn_pr |
premium coupon rate |
2.00% |
|
|
freq_pr |
premium payment frequency |
3 |
quarterly |
|
pr_acc_type |
type of premium accrued interest payment |
1 |
pay accrued interest upon default |
|
acc |
accrual method |
2 |
actual/360 |
|
d_rul |
business day convention |
2 |
next business day |
|
front_fee |
upfront premium payment (% of notional) |
0.20% |
|
|
p_off |
payoff type |
1 |
pay at default |
|
dp_type |
default curve type |
1 |
CDS spread curve |
|
dp_crv |
default curve |
see above |
|
|
dp_para |
default curve parameter table |
see below |
|
|
rate_recover |
recovery rate table |
0.4 |
|
|
hl |
holiday list |
0 |
|
|
dfstd |
discount factor curve |
see above |
|
|
intrp |
interpolation method |
1 |
linear |
|
pos |
trade position |
1 |
buy protection |
|
calc_para |
calculation parameters |
see above |
|
|
stat |
stat list |
1…14 |
|
where the default parameters table is given as
follows:
Default curve parameter table
|
interpolation of default probability curve |
bootstrapping method |
accrual method of time-based default curve |
standard/IMM maturities |
|
1 |
1 |
4 |
2 |
Results
|
Statistics |
Description |
Value |
|
1 |
fair value |
105514.324 |
|
2 |
value of payoff |
158170.0372 |
|
3 |
value of premium |
-52655.71324 |
|
4 |
accrued interest of premium |
-4000 |
|
5 |
fair value minus accrued interest |
109514.324 |
|
6 |
par spread |
0.064193916 |
|
7 |
basis point value of risk-free curve |
-15.95579294 |
|
8 |
number of days that premium accrues |
72 |
|
9 |
next cash flow date |
20-Dec-05 |
|
10 |
previous cash flow date |
20-Sep-05 |
|
11 |
number of remaining cash flows |
13 |
|
12 |
DVOX of par CDS spread curve |
217.4476779 |
|
13 |
rho of recovery rate |
-263.7103043 |
|
14 |
theta |
-134.2151268 |
Example 5 Valuation of a default
swap on user-defined loans and receivables
Suppose in Example 1 the default swap is purchased to
protect loans to and receivables from Company XYZ. The loans and receivables are given in the
following tables:
Loan coupon table
|
effective date |
terminating date |
notional |
rate |
|
1-Dec-2004 |
1-Sep-2006 |
100000 |
0.08 |
|
1-Sep-2005 |
1-Mar-2007 |
50000 |
0.08 |
|
1-Jun-2005 |
1-Jun-2008 |
500000 |
0.1 |
|
1-Jun-2007 |
1-Dec-2010 |
200000 |
0.1 |
Fixed payments (principals & receivables)
|
date |
amount |
|
1-Sep-2006 |
50000 |
|
1-Mar-2007 |
50000 |
|
1-Nov-2008 |
80000 |
|
1-Jun-2009 |
300000 |
|
1-Dec-2010 |
200000 |
Suppose that 30% of both principals and coupons
can be recovered when Company XYZ defaults. The payoff structure is similar to that in
Example 1. In more detail in the case
that Company XYZ defaults during the protection period, for any future fixed
payments Bank B will pay Company A the difference of the outstanding face
values of the fixed payments and whatever is recovered of the outstanding fixed
payments and coupons. Suppose the premium
is paid in fixed amounts scheduled in the following table:
Fixed payments (premium)
|
date |
amount |
|
1-Oct-2006 |
5000 |
|
1-Oct-2007 |
2500 |
|
1-Oct-2008 |
1500 |
Using the function aaCredit_Dswap_fs_sep
we obtain the following results:
aaCredit_Dswap_fs_sep
|
Argument |
Description |
Example Data |
Switch |
|
d_v |
value (settlement) date |
1-Dec-05 |
|
|
contra_d |
CDS contract dates |
see above |
|
|
princ_pr |
premium notional principal |
100000 |
|
|
cpn_pr |
premium coupon rate |
0 |
|
|
freq_pr |
premium payment frequency |
2 |
semi-annual |
|
pr_acc_type |
type of premium accrued interest payment |
1 |
pay accrued interest upon default |
|
acc |
accrual method |
2 |
actual/360 |
|
d_rul |
business day convention |
1 |
no adjustment |
|
prem_fix |
fixed premium payment table |
see above |
|
|
loancpn |
loan coupon payment table |
see above |
|
|
loanfixed_tbl |
loan fixed payment table |
see above |
|
|
acc_fs |
accrual method(s) of bond coupon |
1 |
|
|
payoff_type |
payoff type |
1 |
pay at default |
|
prob_crv |
default probability curve |
see above |
|
|
intrp_prob |
interpolation method of probability curve |
1 |
linear |
|
rate_recover |
recovery rate table |
30% |
|
|
hl |
holiday list |
0 |
|
|
df_crv_std |
discount factor curve |
see above |
|
|
intrp |
interpolation method |
1 |
linear |
|
position |
trade position |
1 |
buy protection |
|
calc_type |
calculation type |
1 |
simplified calculation method |
|
stat |
stat list |
1…14 |
|
Results
|
Statistics |
Description |
Value |
|
1 |
fair value |
18817.7 |
|
2 |
value of payoff |
26831.41 |
|
3 |
value of premium |
-8013.729 |
|
4 |
accrued interest of premium |
-0 |
|
5 |
fair value minus accrued interest |
18817.68 |
|
6 |
par spread |
0.070752 |
|
7 |
basis point value of risk-free curve |
-3.171209 |
|
8 |
number of days that premium accrues |
0 |
|
9 |
next cash flow date |
38991 |
|
10 |
previous cash flow date |
0 |
|
11 |
number of remaining cash flows |
0 |
|
12 |
DV01 of par CDS spread curve |
152.7873 |
|
13 |
rho of recovery rate |
-437.7992 |
|
14 |
theta |
-27.49973 |
References
[1]
Francis, J. C., Frost, J. A. and Whittaker, J.
G., (1999), The Handbook of Credit Derivatives,
[2]
[3]
Luo, L., (2005), ‘Bootstrapping default
probability curves’, Journal of Credit Risk 1
(4), p. 169 – 179.
Disclaimer
With respect to this document,
FinancialCAD Corporation (“FINCAD”) makes no warranty either express or
implied, including, but not limited to, any implied warranty of merchantability
or fitness for a particular purpose. In no event shall FINCAD be liable to
anyone for special, collateral, incidental, or consequential damages in
connection with or arising out of the use of this document or the information
contained in it. This document should not be relied on as a substitute for your
own independent research or the advice of your professional financial,
accounting or other advisors.
This information is subject to change
without notice. FINCAD assumes no responsibility for any errors in this
document or their consequences and reserves the right to make changes to this
document without notice.
Copyright
Copyright © FinancialCAD Corporation 2008.
All rights reserved.