Synthetic CDO Valuation Using Quasi-Analytic Methods
Overview
A collateralized debt obligation (CDO) is a security that is
backed by or linked to a diversified pool of credits. The credits can be
assets, such as bonds or loans, or simply defaultable names, such as companies or
countries. In general, there are two types of CDOs: cash CDOs and synthetic
CDOs. A cash CDO is backed by “true” assets, such as bonds or loans. Its
payoffs, either coupons or principals, come from the actual cash flows of the
assets in the pool. Synthetic CDOs are not backed by cash flows of assets. Instead,
they are linked to their reference entities by credit derivatives, such as
credit default swaps. The payoffs of most synthetic CDOs are only affected by
credit events, e.g., defaults, of the reference entities and are not related to
the actual cash flows of the pool.
A common structure of CDOs involves slicing the credit
risk of the reference pool into a few different risk levels. A “slice” of
credit risk, the credit risk between two risk levels, is called a tranche. The
tranche that absorbs the first loss piece is often called an equity tranche. The
remaining tranches are called mezzanine or senior tranches. Tranches with higher
credit risks support the tranches with lower credit risks.
A typical feature of a cash CDO is the so-called cash flow
waterfall structure where a tranche is paid for its coupon and/or principal
only if all the tranches with lower credit risk have been paid off. Such a
feature requires a match between the incoming coupons and principals of the
pool and the payouts of the tranches. Most
synthetic CDOs don’t have a cash flow waterfall structure. Synthetic CDOs are only
concerned with the default loss. This simplified structure makes structuring,
managing and valuing synthetic CDOs easier than cash CDOs. The important
implication of such a simplified CDO structure is that tranche customization is
possible. Since the payoffs of one tranche don’t depend on the payoffs of other
tranches, it is easy to structure CDOs with any types of tranches, based on an investor’s
risk appetite. This makes synthetic CDOs attractive to both CDO investors and managers
and has helped the rapid development of the CDO market.
Synthetic CDOs without a cash flow waterfall structure are
sometimes called single tranche CDOs. In the rest of this document all CDOs
discussed are single tranche CDOs.
CDO tranches, CDSs on tranches and CDO notes
The risk levels of a synthetic CDO are determined by the
total accumulated loss of the reference pool. A tranche is defined as a certain
loss range. The lower bound of the range is called an attachment point and the
upper bound a detachment point. For example, a 5-10% tranche has an attachment
point of 5% and a detachment point of 10%. When the accumulated loss of the
reference pool is no more than 5% of the total initial notional of the pool,
the tranche will not be affected. However, when the loss has exceeded 5%, any
further loss will be deducted from the tranche’s notional until the detachment
point, 10%, is reached. At this point, the tranche is wiped out.
The most common credit derivatives of synthetic CDOs are credit
default swaps (CDS) and credit-linked notes on CDO tranches. A CDS on a CDO
tranche is, to a certain extent, similar to a single-entity credit default swap
(for single entity CDSs, see the Credit Default Swaps FINCAD Math Reference document). It has a
payoff leg and a premium leg. The buyer of a CDS on a tranche will be
compensated by the seller for any loss to the tranche and in return the buyer
pays a periodic premium to the seller. While the basic structure is similar,
there are two fundamental differences between a tranche CDS and single entity
CDS:
1. In
a single-entity CDS the seller will take the full loss of the reference credit
while in a CDS on a CDO tranche the seller is protected by the tranches with
higher credit risk. In more detail, as
long as the total loss of the reference pool does not exceed the attachment
point of a tranche, the tranche is not affected. Moreover, the loss to a tranche is limited to
its notional, not the total loss of any of the credits in the pool.
2. In
a single-entity CDS the premium notional is fixed during the life of the CDS
while in a CDS on a CDO tranche the premium notional changes. When a tranche suffers a loss, the buyer will
be paid up to the notional of the tranche and at the same time, for most CDOs, the
lost amount will be subtracted from the tranche’s notional. Thus the premium
payment reduces, until the notional reaches 0 when the CDS ends.
A similar comparison can be made between a
tranche CDS and a basket CDS, such as a first-to-default CDS (for details on
basket CDSs see the Basket Default Swaps FINCAD Math Reference document). Like a single entity CDS, a basket CDS allows
only a single credit event and the investor will suffer the full loss if a
credit event occurs. The only difference
between a basket CDS and a single-entity CDS is that in a basket CDS the credit
risk to the investor is from multiple entities. We can say that basket CDSs are more like
single-entity CDSs than tranche CDSs. Particularly,
one should not confuse a first-loss CDS with a first-to-default CDS. A first-loss CDS is a CDS on the equity
tranche of a CDO and, as is pointed out above, it is significantly different
from a first-to-default CDS.
It should be to be pointed out that a first loss CDS is a
CDS on the loss of a portfolio of entities up to a certain level. It doesn’t have to be associated with a formal
CDO structure, although it can always be viewed as a CDS on the equity tranche
of a CDO, i.e., a CDO that has only one tranche, the equity tranche.
Synthetic CDOs consisting only of credit default swaps are
unfunded CDOs. Some synthetic CDOs issue
notes linked to CDO tranches. These CDOs
are funded or partially funded. The buyer of a CDO note pays a certain amount,
the note’s principal, upfront and receives periodic coupon payments from the
CDO that are based on the principal and a fixed coupon rate. If the tranche doesn’t suffer any loss during
the life of the note, the investor will receive a full repayment of the amount
invested at the beginning. However, if
there are defaults in the reference pool and the pool’s accumulated loss
exceeds the attachment point of the linked tranche, the principal will be
reduced and thus the future coupon and the principal repayment will be reduced.
A similar comparison to the above can be made between a CDO
note (also known as a credit-linked note or a tranche-linked note) and a
single-entity credit-linked note. For
details on single entity credit-linked notes see the Credit-Linked Notes and Rating Sensitive Notes
FINCAD Math Reference document.
Some CDO products, such as CDOs on the CDS indices CDX
and ITraxx,
are exchange traded and are standardized. For a standardized CDO, each entity in the
reference pool has the same notional and the same recovery rate. While standardized CDOs are a special class of
CDOs, the homogeneity of their reference pools greatly simplifies their valuation,
and more importantly, speeds up their calculation.
A typical CDO has a reference pool of more than 100
reference entities. Valuation of a CDO
with such a large reference pool is a challenging task. Monte Carlo
simulation has been a useful tool in CDO valuation, but its performance has
always been an obstacle for wide use in the rapidly developing CDO market. Non-Monte Carlo methods have proven to be more
effective than Monte Carlo simulation, thanks in
part to the standardization of the CDO market. Such non-Monte Carlo methods have been
referred to in the literature as quasi-analytic, semi-analytic, or closed-form
methods.
FINCAD provides tools to value both CDSs on tranches and CDO
notes. CDSs on tranches are valued with both
Monte Carlo and quasi-analytic methods. CDO
notes are valued with Monte-Carlo simulation. This document mainly discusses quasi-analytic
methods. For discussions on the
application of Monte Carlo simulation to CDOs see
the Synthetic
CDO Valuation Using Monte Carlo Simulation FINCAD Math Reference
document.
Formulas & Technical Details
Consider a CDO tranche with attachment and detachment points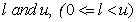 , respectively. Let
, respectively. Let 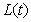 denote the accumulated
loss of the pool at time
denote the accumulated
loss of the pool at time 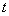 (the current time is 0).
Let
(the current time is 0).
Let 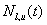 denote the (full) notional
of the tranche at time
denote the (full) notional
of the tranche at time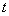 . Then:
. Then:

Credit default swaps on tranches
Consider a CDS on a tranche with its notional being the
tranche’s size. Let  be the time
be the time 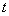 value of the premium leg (also called a fixed leg or a fee
leg) of a credit default swap on the tranche. Let
value of the premium leg (also called a fixed leg or a fee
leg) of a credit default swap on the tranche. Let 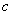 be the annual premium
coupon rate and
be the annual premium
coupon rate and 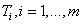 the premium coupon
payment time points. The premium payment amount at a premium payment date is
the product of the premium rate and the current notional of the tranche. For
most synthetic CDO deals, when an entity defaults prior to payment date, the
accrued interest must be paid at the default time. For other less common
synthetic CDOs there is no such accrued premium payment. Accordingly, the
present value of the premium payments can be calculated as
the premium coupon
payment time points. The premium payment amount at a premium payment date is
the product of the premium rate and the current notional of the tranche. For
most synthetic CDO deals, when an entity defaults prior to payment date, the
accrued interest must be paid at the default time. For other less common
synthetic CDOs there is no such accrued premium payment. Accordingly, the
present value of the premium payments can be calculated as
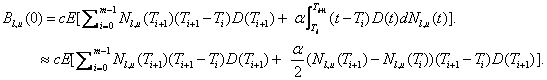
where: 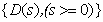 is a risk-free
discount factor curve and the constant
is a risk-free
discount factor curve and the constant 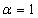 if the accrued premium
is paid when an entity defaults prior to a premium payment date; and
if the accrued premium
is paid when an entity defaults prior to a premium payment date; and 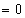 , otherwise.
, otherwise.
Let 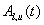 be the time t value of
the payoff leg (also called a default leg or a floating leg or an asset leg) of
the CDS. Then:
be the time t value of
the payoff leg (also called a default leg or a floating leg or an asset leg) of
the CDS. Then:
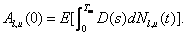
If we assume that compensation is made at the next premium
coupon payment date when default occurs, then the above formula can be detailed
as:
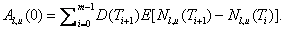
The par CDS spread is then:
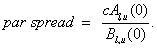
CDO notes (Tranche-linked notes)
For a tranche-linked note, at any coupon payment date, if
the pool loss hasn’t eaten into the tranche yet, the investor will receive a
predetermined coupon based on the initial principal. However, when the tranche suffers a loss, the
note’s notional will be reduced and therefore both the future coupon payments
and the redemption will be reduced.
The one-factor Gaussian (normal) copula model
Default times of different reference entities are
correlated. Ideally, a full correlation
matrix should be used in modeling the correlation between reference entities of
a reference pool. Unfortunately, this is
difficult due to computational intensity, calibration complexity and rarity of
default data. The current popular model
on default correlation is the so-called one-factor Gaussian (normal) copula
model. Under this model the credit
quality of entity 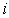 is represented by a
Gaussian random variable:
is represented by a
Gaussian random variable:
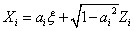
where
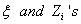 are independent
Gaussian random variables with mean 0 and standard deviation 1 (N(0, 1)) and
are independent
Gaussian random variables with mean 0 and standard deviation 1 (N(0, 1)) and
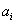 is a constant between
0 and 1. The constant
is a constant between
0 and 1. The constant 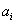 is called the factor
loading of entity
is called the factor
loading of entity 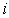 . A higher value of
. A higher value of 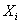 represents a higher credit
quality of the entity. Given a default
probability
represents a higher credit
quality of the entity. Given a default
probability  of the entity one can
then find a threshold value
of the entity one can
then find a threshold value  of
of 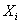 such that:
such that:
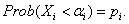
Since 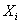 is an N(0,1) variable,
is an N(0,1) variable,
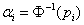 , where
, where 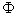 is the cumulative
distribution function of an N(0,1) variable.
With the Gaussian copula model we can determine the credit correlation
easily by simply using the joint probability:
is the cumulative
distribution function of an N(0,1) variable.
With the Gaussian copula model we can determine the credit correlation
easily by simply using the joint probability:
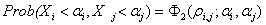
where
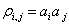 is the correlation of
is the correlation of 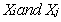 and
and
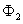 is the cumulative
standard bivariate normal distribution function.
is the cumulative
standard bivariate normal distribution function.
A special case of the Gaussian copula model is the
one for which all factor loadings are equal. For this case each pair of the reference
entities has the same correlation,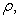 and the factor loading is the square root of the
correlation:
and the factor loading is the square root of the
correlation:
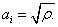
The Fast Fourier Transform (FFT)
In the valuation of a CDO, the key is to calculate the
loss distribution of the reference pool. Let 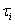 be the default time of
entity
be the default time of
entity 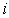 and
and 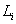 the loss amount when the
entity defaults. Then the total loss of
the reference pool up to a given time horizon
the loss amount when the
entity defaults. Then the total loss of
the reference pool up to a given time horizon  is:
is:
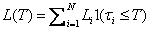
where
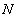 is the number of
entities in the pool and
is the number of
entities in the pool and
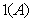 is the indicator
function of
is the indicator
function of 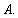
When the reference entities are homogeneous, i.e.,
all entities have the same notional and the same recovery rate, the estimation
of 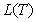 is relatively simple:
the loss distribution can be determined by the number of defaults. However, for a more general case, to
determine the loss amount at a default time we have to trace down the defaulted
entity and hence the simple counting method no longer works. For this case, a more general method is
required.
is relatively simple:
the loss distribution can be determined by the number of defaults. However, for a more general case, to
determine the loss amount at a default time we have to trace down the defaulted
entity and hence the simple counting method no longer works. For this case, a more general method is
required.
Note that to calculate the distribution of 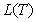 we only need to
determine its characteristic function:
we only need to
determine its characteristic function:
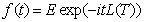 .
.
For this a natural choice is the FFT. When the characteristic function has been
determined, the reverse FFT can be used to back out the loss distribution. For details on calculating loss distributions
using FFT see the paper by A. Debuysscher and M. Szego [5].
The recursion method
The FFT discussed above is general and convenient for
extension, e.g., to the case of random recovery rates. The downside of an FFT
for CDO valuation is its resource intensity in computation, particularly, when
the losses given default of the CDO’s reference entities vary significantly
from entity to entity.
More recently, another type of methods, the so-called
recursion or convolutional methods, have been proposed (for details see
Andersen [1] (2003) and Luo [7] (2006)). Research has shown that the recursion method
is significantly faster than the FFT. For a comparison of computational speed
of the FFT and the recursion see Luo [7] (2006).
The main idea of a recursion method is that when the loss
from default of each entity in a pool is an integer and if the defaults of all
entities are independent, then the loss distribution of an 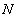 -entity pool can be derived from the loss distribution of a
sub-pool with
-entity pool can be derived from the loss distribution of a
sub-pool with  entities and the default probability of the
entities and the default probability of the 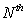 entity convolutionally. Under a factor copula model the
defaults of the reference entities in a pool are conditionally independent
given the common factor. Thus the recursion method can be used to calculate the
conditional loss distribution of the reference pool. When all the conditional
loss probabilities are known, integrating over the common factor one can obtain
the absolute loss distribution of the reference pool.
entity convolutionally. Under a factor copula model the
defaults of the reference entities in a pool are conditionally independent
given the common factor. Thus the recursion method can be used to calculate the
conditional loss distribution of the reference pool. When all the conditional
loss probabilities are known, integrating over the common factor one can obtain
the absolute loss distribution of the reference pool.
In general, losses from defaults are not integers. The
first step in using a recursion method is to approximate non-integer losses
points by integer loss points. Such an algorithm is proposed in Andersen [1] (2003).It is slightly modified in FINCAD
implementation to improve accuracy.
Tranche correlation and base correlation
CDO tranches are actively traded in the market and, especially
for standardized tranches, market quotes are available for par CDO tranche
spreads. A natural question to ask is:
based on a one-factor Gaussian copula model, can we back out correlations from
quoted tranche spreads? In more detail,
given the spread of a CDO tranche is there a correlation that gives the tranche
a par spread equal to the given spread? Such
a correlation is known as a tranche correlation. Research shows that such a correlation does
exist for reasonable par CDS spreads, but, in general, is not unique except the
equity tranche. For the equity tranche (the
tranche with an attachment of 0), the implied correlation is unique (for a
proof see the paper by Burtschell et al [4]). The implied correlation
of an equity tranche is referred to as a base correlation. For a non-equity tranche its base correlation can
also be defined. It is the correlation that
applies to the tranche that has an attachment point of 0 and the same detachment
point of the given tranche. It should be
pointed out that a tranche correlation and a base correlation are tranche
dependent. For different tranches their
correlations can be different.
For a non-equity tranche, the tranche that has an
attachment point of 0 and a detachment point equal to that of the given tranche
is called in this document a base tranche of the given tranche. CDO quotes are
available for regular tranches, but not for base tranches other than the equity
tranche. Hence only for the equity
tranche its base correlation can be calculated directly from the market quotes.
For other tranches their base correlations
cannot be calculated directly and a so-called bootstrapping algorithm must be
used.
To explain the idea of bootstrapping base correlations, consider
the second tranche of a CDO, i.e. the tranche that is beside the equity
tranche. Suppose the base correlation of
the equity tranche has been determined (with a root finding method, e.g., the bisection
method), and we want to determine the base correlation of the second tranche. Note that the loss to the second tranche is
the difference of the loss to its base tranche and the loss to the first
(equity) tranche. Thus the payoff and
premium of the second tranche can also be expressed as the differences of the
base tranche and the equity tranche. Since
the payoff and premium of the equity tranche can be determined from its base
correlation, by matching the calculated par spread and the quoted par spread of
the second tranche, we can solve for the base correlation of the second base
tranche using a root finding procedure. For more details on bootstrapping, the reader
is referred to the paper by McGinty et al [9].
Base correlation mapping
Base correlations are quoted for standardized tranches.
Rigorously speaking, such correlations can only be used to value CDOs that have
the same reference baskets and the same tranche structure. However, since the
value of a CDO tranche is determined by the loss distribution of the reference
portfolio, through proper loss profile matching one can reasonably make use the
quoted base correlations by mapping correlations of standardized tranches to
bespoke tranches. More generally, one can map base correlations of different
CDOs through loss profile matching.
There can be many different ways of matching loss profiles
of CDOs. Here are the two most commonly used ones in the industry.
1.
Match expected loss ratio. For a given base correlation 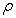 define the expected
loss ratio of a portfolio as:
define the expected
loss ratio of a portfolio as:
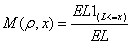
where
 is the portfolio loss
for a certain time horizon,
is the portfolio loss
for a certain time horizon,
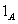 is the indicator of
is the indicator of 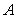 and
and
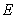 stands for the
expectation with respect to the risk-neutral probability measure.
stands for the
expectation with respect to the risk-neutral probability measure.
Suppose 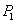 and
and  are two credit portfolios and the base correlation of
portfolio
are two credit portfolios and the base correlation of
portfolio 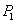 corresponding to detachment
corresponding to detachment 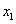 is
is 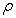 . Then there is a unique point
. Then there is a unique point  such that:
such that:

where
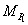 and
and 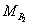 are the expected loss
ratios of portfolios
are the expected loss
ratios of portfolios 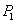 and
and  , respectively. For this loss profile matching an obvious
choice is to select
, respectively. For this loss profile matching an obvious
choice is to select 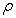 as the base
correlation of portfolio
as the base
correlation of portfolio  at the detachment
at the detachment  . For more details see
the paper of Pugachevsky [10].
. For more details see
the paper of Pugachevsky [10].
This way given a base correlation curve of a benchmark
synthetic CDO, a bespoke base correlation curve can be built. If the bespoke
base correlations at certain detachment points need to be decided,
interpolation can be used. The most popular interpolation method is the
quadratic method. Note that in FINCAD no extrapolation is allowed. In the
interpolation when a detachment point of a bespoke CDO is beyond the base
correlation curve range mapped through the above process, the base correlation
at the closest end point of the curve will be picked.
2. Shift
the base correlation curve. Suppose the
base correlation curve 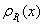 (as a function of its detachment point) of portfolio
(as a function of its detachment point) of portfolio 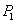 is known. To determine the base correlation curve
is known. To determine the base correlation curve 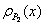 one possibility is simply by shifting:
one possibility is simply by shifting:
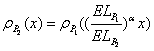
where
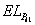 is the expected loss of portfolio
is the expected loss of portfolio 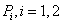 and
and
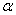 is a scaling factor.
is a scaling factor.
FINCAD Functions
CDO valuation given tranche or base correlations
aaCDO_ST_DS_std_p(d_v,
contra_d, npa_ini, num_ref_ini, num_dflt, tranche_type, tranche_corr, corr_type,
freq_pr, acc, d_rul, dp_type, dp_bskt, intrp_tb, rate_recover, hl, dfstd, intrp,
accu_level, calc_para, stat, tranche_list):
Calculates the fair values and other statistics of a
credit default swap on standardized CDO tranches using a one-factor Gaussian
copula model. The correlation can be either a tranche or a base correlation. Multiple tranches can be valued simultaneously.
Two calculation methods, a fast Fourier transform and a recursion method, are provided.
aaCDO_ST_DS2_std_prem_cf(d_v,
contra_d, npa_ini, num_ref_ini, num_dflt, tranche_type, tranche_corr, corr_type,
freq_pr, acc, d_rul, dp_type, dp_bskt, intrp_tb, rate_recover, hl, dfstd, intrp,
accu_level, calc_para, output_type, tranche_list):
Calculates expected cash flows and their present values of
a credit default swap on standardized CDO tranches using a one-factor Gaussian
copula model. The correlation can be either a tranche or a base correlation.
Two calculation methods, a fast Fourier transform and a recursion method, are
provided.
aaCDO_ST_DS_p(d_v,
contra_d, ref_bskt, tranche_type, tranche_corr, corr_type, freq_pr, acc, d_rul,
dp_type, dp_bskt, intrp_tb, hl, dfstd, intrp, accu_level, calc_para, stat, tranche_list):
Calculates the fair values and other statistics of a
credit default swap on synthetic CDO tranches using a one-factor Gaussian
copula model. The correlation can be
either a tranche or a base correlation. Multiple
tranches can be valued simultaneously. Two calculation methods, a fast Fourier
transform and a recursion method, are provided.
aaCDO_ST_DS2_prem_cf(d_v, contra_d, ref_bskt, tranche_type, tranche_cpn,
corr_type, freq_pr, acc, d_rul, dp_type, dp_bskt, intrp_tb, hl, dfstd, intrp, accu_level,
calc_para, output_type, tranche_list):
Calculates expected cash flows and their present values of
a credit default swap on synthetic CDO tranches using a one-factor Gaussian
copula model. The correlation can be either a tranche or a base correlation.
Two calculation methods, a fast Fourier transform and a recursion method, are
provided.
CDO valuation given factor loadings
aaCDO_ST_DS_fl_p(d_v,
contra_d, ref_bskt, tranche_type, tranche_cpn, freq_pr, acc, d_rul, modl_type, modl_para,
dp_type, dp_bskt, intrp_tb, hl, dfstd, intrp, accu_level, calc_para, stat, tranche_list):
Calculates the fair values and other statistics of a
credit default swap on synthetic CDO tranches using a one-factor copula model.
Different reference entities can have different factor loadings. Multiple tranches can be valued simultaneously.
Two calculation methods, a fast Fourier transform and a recursion method, are
provided.
aaCDO_ST_DS2_fl_prem_cf(d_v,
contra_d, ref_bskt, tranche_type, tranche_cpn, freq_pr, acc, d_rul, modl_type, modl_para,
dp_type, dp_bskt, intrp_tb, hl, dfstd, intrp, accu_level, calc_para, output_type,
tranche_list):
Calculates expected cash flows and their present values of
a credit default swap on synthetic CDO tranches using a one-factor Gaussian
copula model. Different reference entities can have different factor loadings.
Two calculation methods, a fast Fourier transform and a recursion method, are
provided.
aaCDO_ST_DS_dgen_fl_p(d_v,
contra_d, ref_bskt, tranche_type, tranche_dgen, cpn_tbl_tran, pr_fix, freq_pr, acc,
d_rul, modl_type, modl_para, dp_type, dp_bskt, intrp_tb, hl, dfstd, intrp, accu_level,
calc_para, stat, tranche_list):
Calculates the fair values and other statistics of a
credit default swap on synthetic CDO tranches using a one-factor Gaussian
copula model. Different reference
entities can have different factor loadings and the premium leg can have
variable notionals and coupons. Multiple
tranches can be valued simultaneously. Two calculation methods, a fast Fourier
transform and a recursion method, are provided.
aaCDO_ST_DS2_dgen_fl_prem_cf(d_v,
contra_d, ref_bskt, tranche_type, tranche_dgen, cpn_tbl_tran, pr_fix, freq_pr, acc,
d_rul, modl_type, modl_para, dp_type, dp_bskt, intrp_tb, hl, dfstd, intrp, accu_level, calc_para,output_type,
tranche_list):
Calculates expected premium cash flows and their present
values of synthetic CDO tranches using a one-factor Gaussian copula model. Different reference entities can have
different factor loadings and a premium leg can have variable notionals and
coupons. Two calculation methods, a fast Fourier transform and a recursion
method, are provided.
Calculation of sensitivities with respect to individual entities
aaCDO_ST_DS_risk(d_v,
contra_d, ref_bskt, tranche_type, tranche_corr, corr_type, freq_pr, acc, d_rul,
dp_type, dp_bskt, intrp_tb, hl, dfstd, intrp, accu_level, calc_para, tranche_list,
out_type, entity_list):
Calculates for each entity the credit spread and other
sensitivities of credit default swaps on synthetic CDO tranches. A one-factor Gaussian copula model with either
a tranche or a base correlation is used in CDO modeling. Two calculation
methods, a fast Fourier transform and a recursion method, are provided.
aaCDO_ST_DS_fl_risk(d_v,
contra_d, ref_bskt, tranche_type, tranche_cpn, freq_pr, acc, d_rul, modl_type, modl_para,
dp_type, dp_bskt, intrp_tb, hl, dfstd, intrp, accu_level, calc_para, tranche_list,
out_type, entity_list):
Calculates for each name the credit spread and other
sensitivities of credit default swaps on synthetic CDO tranches. A one-factor Gaussian copula model with
variable factor loadings is used in CDO modeling. Two calculation methods, a
fast Fourier transform and a recursion method, are provided.
aaCDO_ST_DS_dgen_fl_risk(d_v,
contra_d, ref_bskt, tranche_type, tranche_dgen, cpn_tbl_tran, pr_fix, freq_pr, acc,
d_rul, modl_type, modl_para, dp_type, dp_bskt, intrp_tb, hl, dfstd, intrp, accu_level, calc_para, tranche_list,
out_type, entity_list):
Calculates for each name the credit spread and other
sensitivities of credit default swaps on synthetic CDO tranches that have
variable notionals and coupons. A
one-factor Gaussian copula model with variable factor loadings is used in CDO
modeling. Two calculation methods, a fast Fourier transform and a recursion
method, are provided.
Calibration of base correlations
aaCDO_ST_DS2_base_ic(d_v,
contra_d, ref_bskt, tranche_sprd, freq_pr, acc, d_rul, dp_type, dp_bskt, intrp_tb,
hl, dfstd, intrp, accu_level, calc_para, tranche_list):
Given par spreads of a credit default swap on synthetic
CDO tranches, calculates the base correlations of the tranches. Two calculation methods, a fast Fourier
transform and a recursion method, are provided.
aaCDO_ST_DS2_std_base_ic(d_v,
contra_d, num_ref_ini, num_dflt, tranche_sprd, freq_pr, acc, d_rul, dp_type, dp_bskt,
intrp_tb, rate_recover, hl, dfstd, intrp,
accu_level, calc_para, tranche_list):
Given par spreads of a credit default swap on standardized
CDO tranches calculates the base correlations of the tranches. Two calculation
methods, a fast Fourier transform and a
recursion method, are provided.
Calculation of loss distributions
aaCredit_loss_prob2_cum(ref_bskt,
prob_bskt, intrp_prob, modl_type, modl_para, low_bound, up_bound, unit_type, time_points,
accu_level, calc_method).
Calculates the cumulative loss distribution of a basket of
defaultable entities using a one-factor Gaussian copula model. Two calculation
methods, a fast Fourier transform and a recursion method, are provided.
aaCredit_loss_prob2_disc(ref_bskt,
prob_bskt, intrp_prob, modl_type, modl_para, time_points, accu_level, calc_method, output_type):
Calculates the loss distribution at discrete loss points
of a basket of defaultable entities using a one-factor Gaussian copula model.
Two calculation methods, a fast Fourier transform and a recursion method, are
provided.
aaCredit_tranche_loss_prob_cum(ref_bskt,
prob_bskt, intrp_prob, tranche_bound, tranche_type, modl_type, modl_para,
time_pts, accu_level, calc_method, output_type):
Given a basket of defaultable entities and tranches of
credit losses, calculate cumulative loss distributions and expected loses of
the tranches using a one-factor Gaussian copula model. Two calculation methods,
a fast Fourier transform and a recursion method, are provided.
Base correlation mapping
aaCDO_ST_baseCorr_map(base_corr,
intrp_gen, ref_bmark, ref_custom, intrp_prob, time_m, detach_custom, map_type,
rescale, accu_level, calc_method):
Map a benchmark base correlation curve to a bespoke base
correlation curve.
Description of Inputs
Functions valuing synthetic CDOs given tranche or base correlations
aaCDO_ST_DS_std_p
aaCDO_ST_DS2_std_prem_cf
aaCDO_ST_DS_p
aaCDO_ST_DS2_prem_cf
|
Input Argument
|
Description
|
|
d_v
|
Valuation date
|
|
contra_d
|
The array contra_d is a table of default swap date(s). It
can have 2 to 7 entries. The first four entries hold in sequence the
terminating date, effective date, odd first coupon date and
next-to-terminating coupon date for premium payments. The last three entries
hold switch values in sequence:
the effective date adjustment method
1.
adjust effective date,
2. do
not adjust effective date
terminating date adjustment method
1.
adjust terminating date,
2. do
not adjust terminating date)
and date generation method
1.
backward,
2.
forward,
3.
IMM dates for premium payments. An IMM date is
the 20th of a month. For example, if the coupon frequency is
quarterly, the IMM dates are: March 20, June 20, Sept. 20 and Dec. 20.
In the table only the
terminating date and the effective date are required. The default values of
the third and fourth entries are 0 and that of the last three entries are 1.
|
|
ref_npa
|
Notional of a reference entity. It is used in the standardized tranche
functions only.
|
|
num_ref_ini
|
Initial number of reference entities. It is used in the standardized tranche
functions only.
|
|
num_dflt
|
Number of defaulted entities up to the valuation date,
inclusive. Used in the standardized
tranche functions only.
|
|
tranche_type
|
Type of tranche (or loss layer) definition - a switch:
1.
proportional (to the initial pool principal),
2.
actual dollar amount.
These two types are mutually convertible. For example, when a proportional tranche
boundary value is converted to an actual dollar amount, the initial tranche
notional is multiplied by the boundary value.
|
|
tranche_corr
|
A 5- to 9-column tranche data table. The required columns are (attachment point,
detachment point, correlation, notional, coupon). The correlation can either be a tranche
correlation or a base correlation, which is determined by the parameter
corr_type. The notional can be any
number between 0 and the size of the tranche. If it is 0, it will be calculated as the
size of the tranche. When a portion of
a tranche, instead of the whole tranche, is traded, the actual traded initial
notional should be entered here. For
the optional columns 6 - 9, their default values are 1 (buy protection), 1
(premium notional is adjusted for loss), 0 and 0, respectively. . The upfront
fee in column 8 is the ratio of the upfront payment amount to the outstanding
notional of a tranche. An upfront payment is a premium that is paid from the
protection buyer to the protection seller at the valuation date. if
contra_d(2) < = d_v or at the effective date if contra_d(2) > d_v,
i.e., if the CDO is forward-start. If
a CDO is not forward-start, an upfront
fee is only used in the par or implied spread calculation and is not included
in the premium valuation. For a forward-start CDO the upfront payment is included
in the premium value of the CDO. Column 9 holds tranche prices, which are
used only for the calculation of implied tranche spreads.
|
|
corr_type
|
Correlation type - a switch:
1.
tranche correlation;
2.
base correlation.
The tranche correlation of a tranche is a
correlation that can be applied to this tranche. A base correlation of a tranche is a
correlation that can be applied to its base tranche, the tranche having an
attachment point of 0 and a detachment point being the same as that of the
given tranche.
|
|
freq_pr
|
Premium payment frequency, a switch.
|
|
acc
|
Accrual method - a switch.
|
|
d_rul
|
Business day convention - a switch.
|
|
dp_type
|
Default curve type – a switch:
1.
a CDS spread curve,
2.
a default probability curve
|
|
dp_bskt
|
A default curve, either a default probability or a CDS
spread curve, can be time-based (the first column >0 and <1000) or
date-based (the first column >=1000). If it is a default probability curve or a
time-based CDS spread curve, the first column has time (in years) or dates. If it is a date-based CDS spread curve, the first two columns have the effective and
terminating dates of the CDS spreads. The
next m columns have default probabilities/CDS spreads, where m is the number
of reference entities. These columns
must be ordered in the same way as in the reference data table. Times and dates (the terminating dates for a
CDS spread curve) must be increasing. For
a time-based curve, the time-accrual method can be put in the third entry of
the table intrp_tb. Probabilities must
be nonnegative, <=1 and nondecreasing. CDS spreads must be nonnegative. For a date-based default probability curve,
the probabilities in the first row must be 0 and the first date must be the
valuation date if there is one. Excel
users may pass term strings to represent time intervals. Term strings must be in the format kB, kD,
kW, kM, or kY where k is an integer and B, D, W, M and Y stands for market
day, calendar day, week, month and year respectively, e.g., 3M = 3 months.
|
|
intrp_tb
|
A default curve parameter table. The array intrp_tb can
have one to six entries. The first entry has the default probability curve
interpolation method. The second entry has the default probability curve
bootstrapping method (see switch sw_1040 in aaCredit_dfltprob_DSSpred2). It
is used only if the default curve type is "par CDS spread curve" (
dp_type =1). If this entry is missing and dp_type=1, the bootstrapping method
will be set to method 1 (assuming constant density). The third entry stores
the time accrual (day counting) method if the default curve is time-based. If
this entry is missing and the default curve is time-based, the time accrual
method will be set to 30/360. If the default curve is not time based, this
entry will be ignored. The fourth to sixth entries store the effective and
terminating date adjustment types and the date generation method of a CDS
curve, respectively. These entries are used only when dp_type = 1. Their
default values are 1.
|
|
rate_recover
|
Recovery rate of all the credits in the credit pool. Used in the standardized tranche functions
only.
|
|
hl
|
Holiday list
|
|
dfstd
|
Discount factor curve.
It may be input as a 2-column, multi-row table (column 1 = date,
column 2 = discount factor), or as a single cell containing a rate. If input
as a single rate, there are three format choices:
1.
a rate (1 row, 1 column); or
2. a
rate and a rate quotation basis (1 row, 2 columns); or
3. a
rate, a rate quotation basis, and an accrual method (1 row, 3 columns).
If the basis or accrual is not provided, they
are assumed to be annual, actual/365. A
2-column flat-rate discount factor curve is constructed internally using the
rate, basis, and accrual method. The last date in the discount factor curve
>= last "date" in the default curve and the terminating date of
the swap
|
|
intrp
|
Interpolation method of the discount factor curve, a
switch.
|
|
accu_level
|
Level of accuracy, a switch. There are four levels of accuracy. For valuation functions the accuracy levels
are determined according to the levels of accuracy in integration. The four accuracy levels correspond to four
different numbers of points, 10, 30, 50 and 100, respectively, that are used
in the Gaussian quadrature of integration.
For base correlation calibration, they are determined according to
accuracy in integration and levels of tolerance in convergence. The four levels correspond to the above numbers
of Gaussian quadrature points and the four tolerance levels, 0.01, 0.001,
0.0001 and 0.00001, respectively.
|
|
calc_para
|
In a fair value calculation function it is a calculation
parameters and premium accrual type table. It can have one or three entries. The first entry has the calculation method
(1 = FFT, 2 = a recursion method). The
second entry is the bump size (in basis points) for DVOX and/or delta
calculation. The third entry has the premium accrual type (1 = pay accrued
premium upon default, 2 = pay no accrual premium upon default). The default
value of the second entry is 1 (basis point) and that of the third entry is 2.
In a cash flow function it is a one or two entry table. It
is similar to above but without the second entry, the entry of a DVOX bump
size.
|
|
stat
|
A list of indicators for fair value and other statistics. It can be any subset of {1,…23}.
|
|
tranche_list
|
List of tranche indicators. It can be any (ascending) subset of {1, 2,
the number of rows of the tranche table}.
|
|
ref_bskt
|
Reference data table. It can have 2 or 3 columns. The first two columns have the notional and
recovery rate of a reference entity. The
optional third column has the default status of an entity (0 = alive, 1 =
defaulted). When the column is
missing, its default value is 0.
|
|
output_type
|
Output type of a premium cash flow table, a switch,
1.
a 6-column table of no-default cash flow table
(tranche ID, date, notional, coupon, no-default interest, accrued interest);
2. a
6-column cash flow table (tranche ID, date, no-default interest, expected
interest, present value, accrued interest);
3. a
16-column extended cash flow table (tranche ID, effective date, terminating
date, notional, coupon, no-default int., no-default fixed premium, total
no-default cash flow, accrued interest, expected interest., expected fixed
premium, total expected cash flow, present value of interest, present value
of fixed premium, total present value,
discount factor). The fixed premium
column has a non-zero value only if the effective date > the valuation
date and the upfront column of the tranche table has a positive value.
4. a
default probability curve
|
For other functions, the definitions for most of
their input parameters are the same as those given in the above table. In the
following, descriptions will only be given for those parameters that don’t
appear in the above table or have different meanings.
Functions valuing synthetic CDOs given factor loadings
aaCDO_ST_DS_fl_p
aaCDO_ST_DS2_fl_prem_cf
aaCDO_ST_DS_dgen_fl_p
aaCDO_ST_DS2_dgen_fl_prem_cf
|
Input Argument
|
Description
|
|
tranche_cpn
|
A 4- to 8-column tranche data table. It is similar to the table tranche_corr (see
the input parameter table above) except that it doesn’t have a correlation
column
|
|
modl_type
|
Model type. There
is only one selection in this release: normal (Gaussian) copula model.
|
|
modl_para
|
An array of factor loading(s). It can have up to N (the number of reference
entities, i.e., rows of ref_bskt) elements. The ith element is the factor loading of the
ith entity. If the table has m< N
elements, the factor loading of any jth (j>=m+1) element is set to the
value of the mth element. Note that if all the pairs of the entities in the
basket have the same correlation, the factor loading of all the entities is
the same, which is the square root of the absolute value of the correlation.
|
|
tranche_dgen
|
A tranche table. The
required columns are (attachment point, detachment point). The columns 3 - 5 are optional. Their
default values are 1 (buy protection), 1 (premium notional is adjusted for
loss) and 0% (no upfront fee), respectively. See tranche_cpn above for the
description of an upfront fee in column 5.
|
|
cpn_tbl_tran
|
A notional and coupon table. It has 2N+2 columns (effective date, terminating
date, notional of tranche 1, coupon of tranche 1, notional of tranche N,
coupon of tranche N), where N is the number of tranches. The terminating date must be ascending and
the terminating date of the ith row must be the same as the effective date in
the (i+1)th row. The notional of a
tranche cannot be larger than the tranche size.
|
|
pr_fix
|
A fixed premium payment table. It can be a single entry
table or an N+1-column table, where N is the number of tranches. If it is single entry table, all tranches
have no fixed premium payments. If it is an N+1-column table, the first
column has payment dates and the (i+1)th column the fixed premium payment of
the ith tranche, i=1...N. Dates must be ascending and fixed premium
payments must be nonnegative. Note
also that an upfront payment of a tranche can be treated as a fixed payment,
but will be used in valuation only if its payment date is later than d_v.
|
|
stat
|
A list of indicators for fair value and other statistics. It can be any subset of {1, 2,…21}.
|
|
output_type
|
Output type of a premium cash flow table, a switch,
1.
an 8-column table of no-default cash flow
table (tranche ID, date, notional, coupon, no-default interest, no-default
fixed payment, total cash flow, accrued interest);
2.
a 5-column expected cash flow table (tranche
ID, date, expected interest, expected fixed payment, total expected cash
flow).
3.
a 5-column present value cash flow table
(tranche ID, date, present value of interest, present value of fixed payment,
total present value);
4.
a 6-column interest cash flow table (tranche
ID, date, no-default interest, expected interest, present value, accrued
interest);
5.
a 16-column extended cash flow table (tranche
ID, effective date, terminating date, notional, coupon, no-default interest,
no-default fixed payment, total no-default cash flow, accrued interest,
expected interest, expected fixed payment, total expected cash flow, present
value of interest, present value of fixed payment, total present value,
discount factor).
6.
a default probability curve
|
Functions for calculating sensitivities for each entity in the reference
pool
aaCDO_ST_DS_std_risk
aaCDO_ST_DS_risk
aaCDO_ST_DS_fl_risk
aaCDO_ST_DS_dgen_fl_risk
|
Input Argument
|
Description
|
|
out_type
|
An output type. In aaCDO_ST_DS_std_risk,
it is a switch with three values:
1.
delta of CDS spread;
2. DVOX
of CDS spread.
3. Jump-to-default
value (value of default),
in aaCDO_ST_DS_risk,
it has four values:
1.
delta of CDS spread;
2. DVOX
of CDS spread;
3. rho
of correlation;
4. Jump-to-default
value (value of default)
and in aaCDO_ST_DS_fl_risk
and aaCDO_ST_DS_dgen_fl_risk,
it has five values:
1.
delta of CDS spread;
2. DVOX
of CDS spread;
3. rho
of correlation;
4. rho
of factor loading;
5. Jump-to-default
value (value of default)
|
|
entity_list
|
A list of entities of the reference pool. In aaCDO_ST_DS_std_risk,
the entity list is any subset of {1…, number of entities minus number of
defaulted entities}, noting that in this case no reference table is given and
only the information on the survived references is available. In other functions the list can be any
subset of {1, 2,...number of entities}.
|
Functions for calibrating base correlations
aaCDO_ST_DS2_std_base_ic
aaCDO_ST_DS2_base_ic
|
Input Argument
|
Description
|
|
tranche_sprd
|
A tranche table with par spreads or implied spreads given
prices. It can have 3 to 5 columns.
The required columns are (attachment point, detachment point, par/implied CDS
spread). For the optional forth and
fifth columns (trading position, upfront payment) their default values are 1
(buy protection), 1 (premium notional is adjusted for loss) and 0%, respectively.
The upfront payment in column 5 is a
fee that is paid from the protection buyer to the protection seller at the
valuation date. An upfront fee, a
number between 0 and 1, is the ratio of the upfront fee amount to the
outstanding notional of the tranche.
|
|
accu_level
|
Level of accuracy, a switch. There are four levels of accuracy. They are determined according to the levels
of accuracy in integration and accuracy of convergence in root finding.
|
|
calc_para
|
It is the same as that of a cash flow function. See the
input parameter description of the function aaCDO_ST_DS2_prem_cf
for details
|
Functions for calculating loss distributions
aaCredit_loss_prob2_cum
aaCredit_loss_prob2_disc
aaCredit_tranche_loss_prob_cum
|
Input Argument
|
Description
|
|
ref_bskt
|
A two-column reference entity data table (notional, recovery
rate)
|
|
intrp_prob
|
The interpolation method of a probability curve; a switch:
1.
linear,
2. exponential
For both interpolation methods, if the default
probability curve is not long enough, the exponential extrapolation method is
always used to extend the curve.
|
|
prob_bskt
|
A basket default probability curve. It is a time-based default probability curve
(time in years, default probability of entity i, i=1, 2 to N), where N is the number of entities
(rows) in the reference entity table ref_bskt.
|
|
low_bound
|
The lower bound of loss range
|
|
up_bound
|
The upper bound of loss range
|
|
unit_type
|
Unit type of loss bounds, a switch:
1.
the lower and upper bounds are proportional to
the total notional of the reference entity pool;
2. the
bounds are in dollar amount.
|
|
time_points
|
Time points (in years) at which loss probabilities are to
be calculated
|
|
calc_method
|
Calculation method. a switch
1.
a fast Fourier transform
2. a
recursion method
|
|
output_type
|
Output type, a switch (used in aaCredit_loss_prob2_disc
only)
1.
remove negligible loss points
2. keep
all loss points
 Note: If the losses given default of the
reference entities are not the same, many extra loss points may be used in
the calculation of the loss probabilities. These points are not actual loss
points, but may still have very small probability values due to approximation
or round off errors. When output type 1 is selected, any loss points with a
loss probability less than 0.00000000001 will not be included in the output
table.
Note: If the losses given default of the
reference entities are not the same, many extra loss points may be used in
the calculation of the loss probabilities. These points are not actual loss
points, but may still have very small probability values due to approximation
or round off errors. When output type 1 is selected, any loss points with a
loss probability less than 0.00000000001 will not be included in the output
table.
|
|
tranche_bound
|
A tranche definition and loss range table. It has four
columns. The first two columns have the tranche attachment point and
detachment point. The third and fourth columns have the lower bound and upper
bound of the tranche loss. The two bounds are the range of the loss for which
the probability is calculated.
|
The function for base correlation mapping
aaCDO_ST_baseCorr_map
|
Input Argument
|
Description
|
|
base_corr
|
A base correlation table (detachment point, base
correlation). Note that a detachment point must be >0 and rigorously
increasing, and a base correlation must be >=0 and <1.
|
|
intrp_gen
|
Interpolation method of a base correlation curve – a
switch.
|
|
ref_bMark
|
The reference data table of the benchmark CDO. It can be a
two-column reference entity data table (notional, recovery rate) or a three column and one row table where
the third column has the number of entities in the basket. Note that for a
three column table, all the reference entities must have the same notional
and the same recovery rate.
|
|
ref_custom
|
Similar to ref_bMark, but
it is the reference table for the bespoke CDO.
|
|
prob_bmark
|
Default probability curve of the benchmark reference
basket. It can be an N+1 column table with N the number of entities, where
the first column has the time horizon and column i+1 has the default
probability of entity i. or a two-column table where the second column has
the default probabilities of each entity in the basket. Note that for t he
second type of table all the entities must have the same default
probabilities.
|
|
intrp_prob
|
See above
|
|
time_m
|
Time to maturity of the CDOs
|
|
detach_custom
|
Detachment points of the custom CDO at which base
correlations are to be calculated.
|
|
map_type
|
Correlation mapping type, a switch. See the section Base
correlation mapping for details.
|
|
accu_level
|
See above
|
|
calc_method
|
See above
|
Description of Outputs
Functions that calculate fair values and other statistics
aaCDO_ST_DS_std_p
aaCDO_ST_DS_p
aaCDO_ST_DS_fl_p
|
Output Statistics
|
Description
|
|
1
|
Fair value
|
|
2
|
Value of payoff
|
|
3
|
Value of premium
|
|
4
|
Accrued interest of premium
|
|
5
|
fair value minus accrued interest
|
|
6
|
Implied spread given price.
Case 1: The input tranche data
table does not have a column of quoted prices.
For this case when the effective date <= the
valuation date, the implied spread of a tranche is the (par) CDS spread that
makes the fair value minus the accrued interest equal the amount of the
tranche’s upfront payment; otherwise, it is the CDS spread that makes the
fair value minus the accrued interest equal 0.
Case 2. The input tranche data
table has a column of tranche prices.
For this case when the effective date <= the
valuation date, the implied spread of a tranche is the CDS spread that makes
the fair value minus the accrued interest equal the amount of the tranche’s
upfront payment plus the given tranche price; otherwise, it is the CDS spread
that makes the fair value minus the accrued interest equal the tranche price.
|
|
7
|
Ratio of par or implied spread and reference credit spread
aggregate. This is the ration of the par spread of a tranche and the sum of
the par CDS spreads of reference entities at maturity.
|
|
8
|
Attachment point
|
|
9
|
Detachment point
|
|
10
|
Tranche size
|
|
11
|
Tranche notional
|
|
12
|
Tranche loss up to the valuation date, inclusive
|
|
13
|
Outstanding tranche notional. This is the difference of the initial
tranche notional and the accumulated loss to the tranche.
|
|
14
|
DVOX of credit default spreads
|
|
15
|
Rho
of recovery rate
|
|
16
|
Rho
of correlations ( rho of factor loadings in aaCDO_ST_DS_fl_p)
|
|
17
|
BPV of risk-free rate
|
|
18
|
Theta
|
|
19
|
Number of days that premium accrues
|
|
20
|
Next coupon date
|
|
21
|
Previous coupon date
|
|
22
|
Number of remaining cash flows
|
|
23
|
Implied upfront fee given premium coupon rate. If the CDO
is not forward-start, it is the upfront fee per one unit notional of a
tranche that makes the upfront payment amount, the fee times the outstanding
notional of a tranche, equal the tranche’s fair value minus its accrued
interest; otherwise it is the upfront fee that makes the fair value of the
tranche minus its accrued interest have a value of 0. If the trading position
of a tranche is selling protection, the upfront payment must be multiplied by
-1 in the calculation.
|
The function aaCDO_ST_DS_dgen_fl_p has
all the above outputs except the statistics 6 and 7.
The outputs are arranged in a two-dimensional array. Different rows correspond to different statistics.
The columns correspond to the tranches in the tranche list tranche_list. The
order of the tranches remains the same as in the list.
Functions that calculate CDO premium cash flows
aaCDO_ST_DS2_std_prem_cf
aaCDO_ST_DS2_prem_cf
aaCDO_ST_DS2_fl_prem_cf
|
table_type
|
Switch
|
Description
|
|
|
1
|
No-default cash flow table
|
A six column table of cash flows (tranche ID, date, notional,
coupon, no-default interest, accrued interest) given that no default occurs
during the life of the CDO.
|
|
|
2
|
Expected cash flow table
|
A six-column expected and present value cash flow table
(tranche ID, date, no-default interest, expected interest, present value, accrued
interest)
|
|
|
3
|
Extended cash flow table
|
A 16-column extended cash flow table (tranche ID, effective
date, terminating date, notional, coupon, no-default interest, no-default
fixed payment, total no-default cash flow, accrued interest, expected
interest, expected fixed payment, total expected cash flow, present value of
interest, present value of fixed payment, total present value, discount
factor). The columns corresponding to
fixed cash flows store the upfront fee payment only. These columns have zero values unless the
CDO is forward-start, i.e., contra_d(2)>d_v.
|
|
|
|
4
|
Default probability curve
|
If the input default curve is a CDS spread curve, it is
the default probability curve generated from the spread curve. Otherwise, it
is simply the default probability curve standardized from the input curve.
|
|
For aaCDO_ST_DS2_dgen_fl_prem_cf, its output table has the
following six types
|
table_type
|
Switch
|
Description
|
|
1
|
No-default cash flow table
|
An 8-column table of no-default cash flow table (tranche
ID, date, notional, coupon, no-default interest, no-default fixed payment,
total cash flow, accrued interest)
|
|
2
|
Expected cash flow table
|
A 5-column expected cash flow table (tranche ID, date,
expected interest, expected fixed payment, total expected cash flow).
|
|
3
|
Cash flow present value table
|
A 5-column cash flow present value table (tranche ID,
date, present value of interest, present value of fixed payment, total
present value);
|
|
4
|
Interest cash flow table
|
A 6-column interest cash flow table (tranche ID, date,
no-default interest, expected interest, present value, accrued interest
|
|
5
|
Extended cash flow table
|
A 16-column extended cash flow table (tranche ID,
effective date, terminating date, notional, coupon, no-default interest, no-default
fixed payment, total no-default cash flow, accrued interest, expected
interest, expected fixed payment, total expected cash flow, present value of
interest, present value of fixed payment, total present value, discount
factor). The columns corresponding to
fixed cash flows store the upfront fee payment only. These columns have zero values unless the
CDO is forward-start, i.e., contra_d(2)>d_v.
|
|
6
|
Default probability curve
|
See the above table for descriptions.
|
Functions that calculate sensitivities on individual reference entities
aaCDO_ST_DS_std_risk
aaCDO_ST_DS_risk
aaCDO_ST_DS_fl_risk
aaCDO_ST_DS_dgen_fl_risk
These functions calculate sensitivity statistics with
respect to individual entities. Their
outputs are two-dimensional arrays. The
rows correspond to the entities given in entity_list and
the columns to entity IDs (the first column) and tranche IDs given in the table
tranche_list.
The tranche order is the
same as that in the input array tranche_list.
Functions that calculate implied base correlations
aaCDO_ST_DS2_std_ic
aaCDO_ST_DS2_ic
The outputs of these base correlation calibration
functions are two dimensional arrays. The
rows correspond to the entities and the columns to tranche IDs given in the
table tranche_list.
The tranche order is the same as that in
the input array tranche_list.
Functions for calculating loss distributions
aaCredit_loss_prob2_cum
aaCredit_loss_prob2_disc
aaCredit_tranche_loss_prob_cum
For aaCredit_loss_prob2_cum, its output table, a 1
by N table with N being the number of points in the input array time_points,
gives for any time point in this array the probability that the total
accumulated loss from time 0 to this time point will fall between the range
low_bound and up_bound.
For aaCredit_loss_prob2_dis, the loss
probabilities are calculated for a set of loss units. It is an M by N table,
where M is the number of loss units and N is the number of points in the input
array time_points . Note that M depends on the reference data table ref_bskt.
If this table is far from being homogeneous, M can be very large. If the output
type is set to “remove negligible loss points”, the extra loss points, which are
not the “true” loss points of the reference pool, will not be included in the
output table. See more details on the input parameters table of these
functions.
For aaCredit_tranche_loss_prob_cum, its outputs
are similar to those of the function aaCredit_loss_prob2_cum
except that the loss probabilities are for losses of tranches instead of losses
of the whole reference portfolio.
Function that maps base correlations of benchmark tranches and bespoke
tranches:
aaCDO_ST_baseCorr_map
The output of this function is a base correlation
curve for the bespoke CDO tranches.
Calculation of risk statistics
DVOX
1.
DVOX on all credit spread curves
of the entities in the reference pool.
This statistic is an output of a fair value
calculation function, e.g., aaCDO_ST_DS_std_p. It is defined as the change in the fair value
per X basis point shift in all the par CDS spread curves of the entities in the
reference pool. In more detail, let 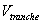 be the fair value of a
CDO derivative. For every entity in the
reference pool, add X basis points to its default curve (if the default curve
is a default probability curve derive a par spread curve first) and build a new
default curve. Then combine these
default curves together to form a basket default curve and use this basket
default curve as an input to revalue the derivative. Let
be the fair value of a
CDO derivative. For every entity in the
reference pool, add X basis points to its default curve (if the default curve
is a default probability curve derive a par spread curve first) and build a new
default curve. Then combine these
default curves together to form a basket default curve and use this basket
default curve as an input to revalue the derivative. Let 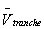 be the new fair value.
The DVOX is then calculated as follows:
be the new fair value.
The DVOX is then calculated as follows:
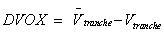
2. DVOX on
a single reference entity.
This statistic is calculated in functions, that
calculate risk statistics exclusively, e.g., aaCDO_ST_DS_std_risk.
It is defined similarly as above, but
only the default curve of the specified entity is shifted X basis point.
See Remark 2 in the section Recursion Method on fast
calculation of DVOXs on individual reference entities.
Delta
Deltas are calculated in functions that output risk statistics
exclusively. The delta on the par CDS
spread of a reference entity is defined as:
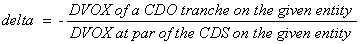
where DVOX at par of a CDS is the DVOX of a CDS with
its premium rate being the par premium rate of the CDS.
Rho of
recovery rate
1.
Rho of recovery
rate of the whole reference pool.
This statistic is calculated in fair value calculation
functions only. It is the change in the
fair value of a CDO derivative per 1% change in the recovery rate. In more
detail, let 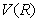 be the fair value of
the derivative at a recovery rate
be the fair value of
the derivative at a recovery rate 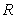 . Then:
. Then:
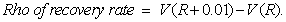
If the recovery rates of the reference entities differ,
the recovery 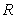 in the above formula
should be replaced with a vector of recovery rates and to bump it simply add
0.01 to every component of the vector.
in the above formula
should be replaced with a vector of recovery rates and to bump it simply add
0.01 to every component of the vector.
2. Rho of
recovery rate of a single reference entity.
This statistic is calculated in functions that only calculate
risk statistics. It is defined similarly
as above, but only the recovery rate of the specified entity is bumped 1%. If a
function, e.g., aaCDO_ST_DS_std_risk, has only one recovery
rate as an input for all the reference entities, such a risk statistic is not
calculated.
Rho of
correlation
This statistic is an output of functions that take in
a correlation and calculate fair values. It is the change in the fair value of a CDO
derivative per 1% change in the correlation. In more detail, let  be the fair value of
the CDO derivative at the correlation
be the fair value of
the CDO derivative at the correlation Then:
Then:

Rho of
factor loading
1.
Rho of
factor loadings on all the reference entities.
This statistic is an output of functions that take in
factor loadings and calculate fair values. It is the change in the fair value of the CDO
derivative per 10% increase in the factor loadings of all the reference
entities. In more detail, let 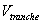 be the fair value of
the CDO derivative. For all the entities
in the reference pool add 0.1 to their factor loadings. Then revalue the derivative to get a new fair
value
be the fair value of
the CDO derivative. For all the entities
in the reference pool add 0.1 to their factor loadings. Then revalue the derivative to get a new fair
value 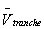 . The rho of factor
loading is then calculated as follows:
. The rho of factor
loading is then calculated as follows:
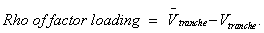
2. Rho of
factor loading on a single reference entity.
This statistic is an output of functions that have a
factor loading table as an input and calculate risk statistics only. It is defined similarly as above, but only the
factor loading of a specified entity is bumped 10%.
Theta
The theta of a CDO derivative is the change in the
fair value of the derivative per one day increase of the valuation date. Let 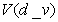 be the fair value of
the derivative. Then:
be the fair value of
the derivative. Then:
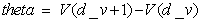
BPV
The BPV (basis point value) of a risk free discount
factor curve is the change in the fair value of a CDO derivative when the
risk-free discount factor curve is shifted up one basis point. To shift up a discount factor curve simply add
one basis point to every point of the corresponding spot rate curve of the
discount factor curve.
Jump-to-default value
The jump-to-default value, also known as the value on
default (VOD), of a tranche position of a synthetic CDO is the sensitivity of
the CDO resulting from an instant default of an entity in the reference basket,
keeping all other credit spreads in the reference basket unchanged. It is
calculated as the sum of the loss amount of the entity which is assumed to
default instantly and the change of the CDO’s fair value after and before the
default of the entity. For example, for a protect seller position the loss
amount is the negative of the loss given default of the reference entity. For
the second part, calculate the fair value of the tranche and then recalculate
it with the default status to default of the entity for which its VOD is to be
calculated. The second part is simply the difference of the tranche’s value of
the second and the first calculation.
Examples
Context examples are given below for various types of CDOs
on valuation, calibration of implied base correlations and delta hedging.
Example 1: CDOs with no
upfront fee payments and no historical defaults
Consider a standardized synthetic CDO with three tranches,
0%-3%, 3%-10% and 10%-15%. The reference
pool has 125 names and each has a notional of 1000000. An investor bought the whole equity tranche and
to hedge it he sold the whole mezzanine tranche 3-10%. For the equity tranche, whenever a reference
name defaults he will be compensated for the loss and at the same time the
notional of his premium payment will be reduced by the lost amount. For the mezzanine tranche, when the
accumulated loss reaches 3% of the total notional of the pool, he has to pay to
the buyer of the tranche any loss to the tranche and at the same time he will
receive less premium payment: the
premium notional of the mezzanine tranche will be reduced by the loss to this
tranche. Suppose all the reference names
have the same flat CDS spread, 0.5% and the same recovery rate, 40%. Other details of the CDO and the required data
are shown in the following six tables.
aaCDO_ST_DS_std_p
|
Argument
|
Description
|
Example Data
|
Switch
|
|
d_v
|
Valuation date
|
1-Dec-2006
|
|
|
contra_d
|
CDS date table
|
see below
|
|
|
ref_npa
|
Notional of a reference entity
|
1000000
|
|
|
num_ref_ini
|
Initial number of reference entities
|
125
|
|
|
num_dflt
|
Number of defaulted entities up to the valuation date
|
0
|
|
|
tranche_type
|
Type of a tranche (or loss layer) definition
|
1
|
proportional
|
|
tranche_corr
|
Tranche table
|
see below
|
|
|
corr_type
|
Correlation type
|
2
|
base correlation
|
|
freq_pr
|
Premium payment frequency
|
3
|
quarterly
|
|
acc
|
Accrual method
|
2
|
act./360
|
|
d_rul
|
Business day convention
|
2
|
next business day
|
|
dp_type
|
Default curve type
|
1
|
par CDS spread curve
|
|
dp_bskt
|
Par CDS spread curve
|
see below
|
|
|
intrp_tb
|
Default curve parameter table
|
see below
|
|
|
rate_recover
|
Recovery rate
|
0.4
|
|
|
hl
|
A holiday list
|
0
|
|
|
dfstd
|
The discount factor curve
|
see below
|
|
|
Intrp
|
Interpolation method of the discount factor curve, a
switch.
|
1
|
linear
|
|
accu_level
|
Level of accuracy
|
2
|
accuracy level 2
|
|
calc_para
|
Calculation parameter table
|
see below
|
|
|
stat
|
List of statistics
|
{1, 2,…,23}
|
|
|
tranche_list
|
Tranche list
|
see below
|
|
CDS Date Table
|
Terminating date
|
Effective date
|
First coupon date
|
Next to last coupon date
|
Effective date adjustment
|
Terminating date adjustment
|
Date generation method
|
|
20-Dec-2010
|
1-Dec-2005
|
0
|
0
|
2
|
2
|
3
|
|
|
|
|
|
Switch: no adjustment
|
Switch: no adjustment
|
Switch: IMM date generation
|
Tranche Table
|
Attachment
|
Detachment
|
Base Correlation
|
Notional
|
Coupon
|
Position
|
Switch
|
|
0
|
0.03
|
0.35
|
0
|
0.1
|
1
|
Buy protection
|
|
0.03
|
0.1
|
0.38
|
0
|
0.02
|
2
|
Sell protection
|
|
0.1
|
0.15
|
0
|
0
|
0
|
1
|
Buy protection
|
Reference Entity CDS Spread Table
|
Effective Date
|
Terminating Date
|
CDS Spread of Entity 1
|
CDS Spread of Entity 2
|
CDS Spread of Entity 3
|
CDS Spread of Entity …
|
|
1-Oct-2006
|
1-Oct-2010
|
0.005
|
0.005
|
0.005
|
…
|
Default Curve Parameter Table
|
interpolation of
default probability curve
|
bootstrapping method
|
accrual method of
time-based default curve
|
effective date
adjustment
|
maturity date
adjustment
|
date generation
method
|
|
1
|
1
|
4
|
2
|
2
|
3
|
Risk-free Discount Factor Curve
|
Date
|
Discount factor
|
|
1-Dec-2006
|
1
|
|
1-Jun-2007
|
0.971285862
|
|
1-Dec-2007
|
0.943396226
|
|
1-Dec-2008
|
0.88999644
|
|
1-Dec-2009
|
0.839619283
|
|
1-Dec-2011
|
0.747258173
|
|
1-Dec-2016
|
0.558394777
|
|
1-Dec-2020
|
0.417265061
|
Calculation Parameters and Premium Accrual Type Table
|
Calculation method
|
Bump size
|
Premium accrual type
|
|
2
|
1
|
1
|
Tranche List
To value the tranche portfolio call the function aaCDO_ST_DS_std_p,
Results
|
Output Statistics
|
Description
|
Tranche 1
|
Tranche 2
|
|
1
|
Fair value
|
125825.44
|
-30885.52
|
|
2
|
Value of payoff
|
1278041.58
|
-679223.77
|
|
3
|
Value of premium
|
-1152216.14
|
648338.25
|
|
4
|
Accrued interest of premium
|
-75000.00
|
35000.00
|
|
5
|
Fair value minus accrued interest
|
200825.44
|
-65885.52
|
|
6
|
Par spread
|
11.86%
|
2.21%
|
|
7
|
Ratio of par spread and reference credit spread aggregate
|
18.98%
|
3.54%
|
|
8
|
Attachment point
|
0.00
|
3750000
|
|
9
|
Detachment point
|
3750000.00
|
12500000
|
|
10
|
Tranche size
|
3750000.00
|
8750000
|
|
11
|
Tranche notional
|
3750000.00
|
8750000
|
|
12
|
Tranche loss up to the valuation date, inclusive
|
0.00
|
0
|
|
13
|
Outstanding tranche notional
|
3750000.00
|
8750000
|
|
14
|
DVOX of credit default spreads
|
21067.43
|
-17928.86
|
|
15
|
Rho
of recovery rate
|
4453.10
|
60.88
|
|
16
|
Rho
of correlations or factor loading
|
-22976.17
|
-4168.75
|
|
17
|
BPV of risk-free rate
|
-18.02
|
34.01
|
|
18
|
Theta
|
-1030.13
|
660.26
|
|
19
|
Number of days that premium accrues
|
72.00
|
72.00
|
|
20
|
Next coupon date
|
20-Dec-2006
|
20-Dec-2006
|
|
21
|
Previous coupon date
|
20-Sep-2006
|
20-Sep-2006
|
|
22
|
Number of remaining cash flows
|
17.00
|
17.00
|
|
23
|
Implied upfront fee given coupon
|
5.355345%
|
0.752977%
|
To round check par spreads simply replace the coupons
of tranches 1 and 2 in the input tranche data table with the output par spreads
and set the statistic list to the single number 5 (the statistic fair value
minus accrued interest) and then rerun the function. The outputs for both tranche
1 and 2 should be 0.
To round check the implied upfront fee, simply
multiply the size and the implied upfront fee of a tranche. For example for
tranche 1 this is:

which equals the fair value minus accrued interest of
tranche 1. To round check tranche 2 a negative sign should be applied to the
result since the tranche has a position of selling protection.
To view the cash flows of the premium legs call the
function aaCDO_ST_DS2_std_prem_cf
with table_type = 3. Here is the output premium cash flow table:
Results
|
ID
|
Date
|
No-default Interest
|
Expected Interest
|
Present Value
|
Accrued Interest
|
|
1
|
20-Dec-2006
|
-94791.67
|
-94708.61
|
-94424.71
|
-75000.00
|
|
1
|
20-Mar-2007
|
-93750.00
|
-91271.52
|
-89701.93
|
0.00
|
|
1
|
20-Jun-2007
|
-95833.33
|
-89988.17
|
-87143.66
|
0.00
|
|
1
|
20-Sep-2007
|
-95833.33
|
-86953.60
|
-82985.84
|
0.00
|
|
1
|
20-Dec-2007
|
-94791.67
|
-83251.38
|
-78308.26
|
0.00
|
|
1
|
20-Mar-2008
|
-94791.67
|
-80692.29
|
-74829.76
|
0.00
|
|
1
|
20-Jun-2008
|
-95833.33
|
-79133.92
|
-72322.41
|
0.00
|
|
1
|
22-Sep-2008
|
-97916.67
|
-78457.84
|
-70628.49
|
0.00
|
|
1
|
22-Dec-2008
|
-94791.67
|
-73766.69
|
-65438.28
|
0.00
|
|
1
|
20-Mar-2009
|
-91666.67
|
-69387.95
|
-60711.15
|
0.00
|
|
1
|
22-Jun-2009
|
-97916.67
|
-72103.14
|
-62151.35
|
0.00
|
|
1
|
21-Sep-2009
|
-94791.67
|
-67904.06
|
-57678.98
|
0.00
|
|
1
|
21-Dec-2009
|
-94791.67
|
-66117.40
|
-55346.14
|
0.00
|
|
1
|
22-Mar-2010
|
-94791.67
|
-64404.07
|
-53170.42
|
0.00
|
|
1
|
21-Jun-2010
|
-94791.67
|
-62758.82
|
-51089.56
|
0.00
|
|
1
|
20-Sep-2010
|
-94791.67
|
-61176.74
|
-49097.29
|
0.00
|
|
1
|
20-Dec-2010
|
-94791.67
|
-59653.40
|
-47187.91
|
0.00
|
|
2
|
20-Dec-2006
|
44236.11
|
44235.64
|
44103.03
|
35000.00
|
|
2
|
20-Mar-2007
|
43750.00
|
43705.37
|
42953.77
|
0.00
|
|
2
|
20-Jun-2007
|
44722.22
|
44564.33
|
43155.66
|
0.00
|
|
2
|
20-Sep-2007
|
44722.22
|
44403.63
|
42377.45
|
0.00
|
|
2
|
20-Dec-2007
|
44236.11
|
43731.00
|
41134.44
|
0.00
|
|
2
|
20-Mar-2008
|
44236.11
|
43517.73
|
40356.04
|
0.00
|
|
2
|
20-Jun-2008
|
44722.22
|
43761.20
|
39994.42
|
0.00
|
|
2
|
22-Sep-2008
|
45694.44
|
44453.69
|
40017.63
|
0.00
|
|
2
|
22-Dec-2008
|
44236.11
|
42772.14
|
37943.08
|
0.00
|
|
2
|
20-Mar-2009
|
42777.78
|
41104.96
|
35964.88
|
0.00
|
|
2
|
22-Jun-2009
|
45694.44
|
43619.11
|
37598.74
|
0.00
|
|
2
|
21-Sep-2009
|
44236.11
|
41937.13
|
35622.19
|
0.00
|
|
2
|
21-Dec-2009
|
44236.11
|
41647.29
|
34862.48
|
0.00
|
|
2
|
22-Mar-2010
|
44236.11
|
41353.03
|
34140.04
|
0.00
|
|
2
|
21-Jun-2010
|
44236.11
|
41053.95
|
33420.45
|
0.00
|
|
2
|
20-Sep-2010
|
44236.11
|
40749.82
|
32703.70
|
0.00
|
|
2
|
20-Dec-2010
|
44236.11
|
40441.00
|
31990.24
|
0.00
|
 Note that in the call to the above cash flow
function, the parameter table calc_para must be
replaced with the following table
Note that in the call to the above cash flow
function, the parameter table calc_para must be
replaced with the following table
Calculation Parameters and Premium Accrual Type Table
|
Calculation method
|
Premium accrual type
|
|
2
|
1
|
Example 2: CDOs with an
upfront fee payment
Suppose in Example 1 the tranches are to be traded and the
equity tranche has a 5% upfront fee, a fee that is paid to the protection
seller at the valuation date. Then the tranche table should be modified as follows:
Tranche Table
|
Attachment
|
Detachment
|
Correlation
|
Notional
|
Coupon
|
Position
|
Notional Adjustment Method
|
Upfront Fee
|
|
0
|
0.03
|
0.35
|
0
|
0.1
|
1
|
1
|
5%
|
|
0.03
|
0.1
|
0.38
|
0
|
0.02
|
2
|
1
|
0
|
|
0.1
|
0.15
|
0
|
0
|
0
|
1
|
1
|
0
|
Since for a non-forward-start CDO an upfront payment
of a tranche is not counted as part of the fair value in a FINCAD CDO function,
the outputs are the same as those of example 1 except for the par CDS spreads
and the ratios of par spread aggregate which are given below:
Results
|
Output Statistics
|
Description
|
Tranche 1
|
Tranche 2
|
|
6
|
Par spread
|
10.12%
|
2.21%
|
|
7
|
Ratio of par spread and reference credit spread aggregate
|
16.20%
|
3.54%
|
 Note that the outputs of tranche 2 are the same
as those in example 1. This is obvious since tranche 2 doesn’t have an upfront fee.
Note that the outputs of tranche 2 are the same
as those in example 1. This is obvious since tranche 2 doesn’t have an upfront fee.
Example 4: CDOs with
historical defaults
Suppose in Example 1 five of the reference entities have
defaulted. To value the CDO, in the
input parameter table of Example 1 set the number of defaults to 5 and replace
the default curve with a curve of 120 entities. Suppose the CDS contract dates
are given as follows
CDS Dates Table
|
Terminating date
|
Effective date
|
First coupon date
|
Next to last coupon date
|
Effective date adjustment
|
Terminating date adjustment
|
Date generation method
|
|
1-Sep-2010
|
1-Sep-2004
|
0
|
0
|
1
|
1
|
3
|
Then call the same function to get the
following results:
Results
|
Output Statistics
|
Description
|
Tranche 1
|
Tranche 2
|
|
1
|
Fair value
|
229881.17
|
-685813.37
|
|
2
|
Value of payoff
|
406159.91
|
-1275745.18
|
|
3
|
Value of premium
|
-176278.74
|
589931.81
|
|
4
|
Accrued interest of premium
|
-15000.00
|
35000.00
|
|
5
|
Fair value minus accrued interest
|
244881.17
|
-720813.37
|
|
6
|
Par spread
|
0.2518
|
0.0460
|
|
7
|
Ratio of par spread and reference credit spread aggregate
|
0.4197
|
0.0766
|
|
8
|
Attachment point
|
0.00
|
3750000.00
|
|
9
|
Detachment point
|
3750000
|
12500000
|
|
10
|
Tranche size
|
3750000
|
8750000
|
|
11
|
Tranche notional
|
3750000
|
8750000
|
|
12
|
Tranche loss up to the valuation date, inclusive
|
3000000
|
0
|
|
13
|
Outstanding tranche notional
|
750000
|
8750000
|
|
14
|
DVOX of credit default spreads
|
4560.18789
|
-25625.675
|
|
15
|
Rho
of recovery rate
|
9039.54836
|
16855.5286
|
|
16
|
Rho of correlations or factor loading
|
-8428.8721
|
9191.3896
|
|
17
|
BPV of risk-free rate
|
-26.877809
|
141.064217
|
|
18
|
Theta
|
-253.6743
|
952.160623
|
|
19
|
Number of days that premium accrues
|
72
|
72
|
|
20
|
Next coupon date
|
20-Dec-2006
|
20-Dec-2006
|
|
21
|
Previous coupon date
|
20-Sep-2006
|
20-Sep-2006
|
|
22
|
Number of remaining cash flows
|
16
|
16
|
|
23
|
Par upfront fee ratio
|
0.32650823
|
0.08237867
|
Example 5: Calibration of
base correlations
Suppose in example 1 the par spreads of tranches 1 and 2
are 12% and 2%, respectively, but the base correlations are unknown. To
calculate the base correlations that are implied from the par spreads, we can
call the function aaCDO_ST_DS2_std_base_ic. The input tables are given in the following
three tables.
aaCDO_ST_DS_std_base_ic
|
Argument
|
Description
|
Example Data
|
Switch
|
|
d_v
|
Valuation date
|
1-Dec-2006
|
|
|
contra_d
|
CDS date table
|
see example 1
|
|
|
num_ref_ini
|
Initial number of reference entities.
|
125
|
|
|
num_dflt
|
Number of defaulted entities up to the valuation date
|
0
|
|
|
tranche_sprd
|
Tranche table
|
see below
|
|
|
freq_pr
|
Premium payment frequency
|
3
|
Quarterly
|
|
acc
|
Accrual method
|
2
|
act./360
|
|
d_rul
|
Business day convention
|
2
|
next business day
|
|
dp_type
|
Default curve type
|
1
|
par CDS spread curve
|
|
dp_bskt
|
Par CDS spread curve
|
see example 1
|
|
|
intrp_tb
|
Default curve parameter table
|
see example 1
|
|
|
rate_recover
|
Recovery rate
|
0.4
|
|
|
hl
|
Holiday list
|
0
|
|
|
dfstd
|
The discount factor curve
|
see example 1
|
|
|
intrp
|
Interpolation method of the discount factor curve, a
switch.
|
1
|
Linear
|
|
accu_level
|
Level of accuracy
|
2
|
accuracy level 2
|
|
calc_para
|
Calculation method and premium accrual type table
|
See below
|
|
|
tranche_list
|
Tranche list
|
see example 1
|
|
Tranche Table
|
Attachment
|
Detachment
|
Spread
|
|
0
|
0.03
|
0.12
|
|
0.03
|
0.1
|
0.02
|
Calculation Method and Premium Accrual Type Table
|
Calculation method
|
Premium accrual type
|
|
2
|
1
|
Other input tables are the same as those in example
1. The results are shown below:
Output Table Results
|
Tranche ID
|
Base Correlation
|
Number of Internal Function
Calls
|
Convergence
(0 = converged)
|
|
1
|
0.3442
|
13
|
0
|
|
2
|
0.4145
|
26
|
0
|
 Note that the calibrated base correlations are
slightly different from those in the input tranche table in example 1. This is
because the spreads in the tranche table of this example are slightly different
from the par spreads of the tranches (see the outputs of example 1 corresponding
to the statistic 6).
Note that the calibrated base correlations are
slightly different from those in the input tranche table in example 1. This is
because the spreads in the tranche table of this example are slightly different
from the par spreads of the tranches (see the outputs of example 1 corresponding
to the statistic 6).
Example 6: A CDO of variable
reference notionals and recovery rates
Suppose in example 1 the CDO is not standardized and its
reference entity pool has 10 names with their notionals and recovery rates
given as in the following table:
Notional and Recovery Rate Table
|
Notional
|
Recovery Rate
|
|
1000000
|
0.4
|
|
1000000
|
0.4
|
|
1000000
|
0.4
|
|
2000000
|
0.4
|
|
2000000
|
0.4
|
|
2000000
|
0.3
|
|
2000000
|
0.3
|
|
3000000
|
0.3
|
|
3000000
|
0.3
|
|
3000000
|
0.3
|
Suppose also that CDS spread curves of the entities
are:
Par CDS Spread Curve
|
|
Names
|
|
Dates
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Effective Date
|
Maturity Date
|
|
|
|
|
|
|
|
|
|
|
|
1-Dec-2006
|
1-Dec-2010
|
0.02
|
0.02
|
0.01
|
0.03
|
0.04
|
0.02
|
0.05
|
0.03
|
0.02
|
0.02
|
Moreover, the coupon rates of tranche 1 and tranche 2
are 5% and 2%, their tranche correlations are 0.35 and 0.38, and their upfront
fees are 30% and 10%, respectively. To value the CDO, call the function aaCDO_ST_DS_p
with the following input tables:
aaCDO_ST_DS_p
|
Argument
|
Description
|
Example Data
|
Switch
|
|
d_v
|
Valuation date
|
1-Dec-2006
|
|
|
contra_d
|
CDS date table
|
see example 1
|
|
|
ref_bskt
|
Reference notional and recovery rate table
|
see above
|
|
|
tranche_type
|
Type of a tranche (or loss layer) definition
|
1
|
proportional
|
|
tranche_corr
|
Tranche table
|
see below
|
|
|
corr_type
|
Correlation type
|
1
|
tranche correlation
|
|
freq_pr
|
Premium payment frequency
|
3
|
Quarterly
|
|
acc
|
Accrual method
|
2
|
act./360
|
|
d_rul
|
Business day convention, a switch.
|
2
|
next business day
|
|
dp_type
|
Default curve type
|
1
|
par CDS spread curve
|
|
dp_bskt
|
Par CDS spread curve
|
see above
|
|
|
intrp_tb
|
Default curve parameter table
|
see example 1
|
|
|
hl
|
holiday list
|
0
|
|
|
dfstd
|
The discount factor curve
|
|
|
|
intrp
|
Interpolation method of the discount factor curve, a
switch.
|
1
|
linear
|
|
accu_level
|
Level of accuracy
|
2
|
accuracy level 2
|
|
calc_para
|
Calculation parameter table
|
See example 1
|
|
|
stat
|
Stat list
|
{1, 2,…,23}
|
|
|
tranche_list
|
Tranche list
|
1, 2
|
|
Tranche Table
|
Attachment
|
Detachment
|
Tranche Correlation
|
Notional
|
Coupon
|
Position
|
Notional adjustment method
|
Upfront fee
|
|
0
|
0.1
|
0.35
|
0
|
0.05
|
1
|
1
|
0.3
|
|
0.1
|
0.2
|
0.38
|
0
|
0.02
|
2
|
1
|
0.1
|
|
0.2
|
0.3
|
0
|
0
|
0
|
1
|
1
|
0
|
Results
|
Output Statistics
|
Description
|
Tranche 1
|
Tranche 2
|
|
1
|
Fair value
|
684586.66
|
-336820.42
|
|
2
|
Value of payoff
|
960530.33
|
-472931.00
|
|
3
|
Value of premium
|
-275943.66
|
136110.58
|
|
4
|
Accrued interest of premium
|
-20000.00
|
8000.00
|
|
5
|
Fair value minus accrued interest
|
704586.66
|
-344820.42
|
|
6
|
Par spread
|
0.07
|
0.04
|
|
7
|
Ratio of par spread and reference credit spread aggregate
|
0.27
|
0.16
|
|
8
|
Attachment point
|
0.00
|
2000000.00
|
|
9
|
Detachment point
|
2000000.00
|
4000000.00
|
|
10
|
Tranche size
|
2000000.00
|
2000000.00
|
|
11
|
Tranche notional
|
2000000.00
|
2000000.00
|
|
12
|
Tranche loss up to the valuation date, inclusive
|
0.00
|
0.00
|
|
13
|
Outstanding tranche notional
|
2000000.00
|
2000000.00
|
|
14
|
DVOX of credit default spreads
|
2341.28
|
-1876.69
|
|
15
|
Rho
of recovery rate
|
5504.05
|
871.72
|
|
16
|
Rho
of correlations or factor loading
|
-8042.14
|
727.70
|
|
17
|
BPV of risk-free rate
|
-113.00
|
73.29
|
|
18
|
Theta
|
-515.42
|
335.54
|
|
19
|
Number of days that premium accrues
|
72.00
|
72.00
|
|
20
|
Next coupon date
|
39071.00
|
39071.00
|
|
21
|
Previous coupon date
|
38980.00
|
38980.00
|
|
22
|
Number of remaining cash flows
|
17.00
|
17.00
|
|
23
|
Implied upfront fee given premium coupon
|
0.35229333
|
0.172410211
|
Example 7: A CDO with variable reference notionals, recovery rates and
defaulted entities
Suppose in Example 6, the reference entity 4 defaulted
sometime after the CDO started trading. Suppose also the contract dates are
given as in Example 4. Then the reference table needs a default status column
as is shown below:
Reference Notional and Recovery Rate Table
|
Notional
|
Recovery Rate
|
Default Status (0=no,
1 =yes)
|
|
1000000
|
0.4
|
0
|
|
1000000
|
0.4
|
0
|
|
1000000
|
0.4
|
0
|
|
2000000
|
0.4
|
1
|
|
2000000
|
0.4
|
0
|
|
2000000
|
0.3
|
0
|
|
2000000
|
0.3
|
0
|
|
3000000
|
0.3
|
0
|
|
3000000
|
0.3
|
0
|
|
3000000
|
0.3
|
0
|
Results
|
Output Statistics
|
Description
|
Tranche 1
|
Tranche 2
|
|
1
|
Fair value
|
298361.62
|
-530327.37
|
|
2
|
Value of payoff
|
400815.95
|
-650501.47
|
|
3
|
Value of premium
|
-102454.34
|
120174.10
|
|
4
|
Accrued interest of premium
|
-8000.00
|
8000.00
|
|
5
|
Fair value minus accrued interest
|
306361.62
|
-538327.37
|
|
6
|
Par spread
|
0.09
|
0.08
|
|
7
|
Ratio of par spread and reference credit spread aggregate
|
0.37
|
0.35
|
|
8
|
Attachment point
|
0.00
|
2000000.00
|
|
9
|
Detachment point
|
2000000.00
|
4000000.00
|
|
10
|
Tranche size
|
2000000.00
|
2000000.00
|
|
11
|
Tranche notional
|
2000000.00
|
2000000.00
|
|
12
|
Tranche loss up to the valuation date, inclusive
|
1200000.00
|
0.00
|
|
13
|
Outstanding tranche notional
|
800000.00
|
2000000.00
|
|
14
|
DVOX of credit default spreads
|
927.48
|
-1958.66
|
|
15
|
Rho
of recovery rate
|
10250.25
|
4449.53
|
|
16
|
Rho
of correlations or factor loading
|
-3571.70
|
3679.82
|
|
17
|
BPV of risk-free rate
|
-45.21
|
92.46
|
|
18
|
Theta
|
-216.62
|
382.34
|
|
19
|
Number of days that premium accrues
|
72.00
|
72.00
|
|
20
|
Next coupon date
|
39071.00
|
39071.00
|
|
21
|
Previous coupon date
|
38980.00
|
38980.00
|
|
22
|
Number of remaining cash flows
|
16.00
|
16.00
|
|
23
|
Implied upfront fee given premium coupon
|
0.38295202
|
0.269163684
|
Example 8: A CDO with factor loadings
Suppose in example 6 neither correlation nor base
correlation is available, but the betas of the reference names can be obtained.
To value the CDO we can scale the betas
so that they are between -1 and 1 and use them as factor loadings. Suppose the factor loadings are shown as in
the following table:
Model Parameter Table
|
Name
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Factor Loading
|
0.5
|
0.6
|
0.4
|
0.7
|
0.8
|
0.2
|
0.6
|
0.5
|
0.3
|
0.1
|
To value the CDO call the function aaCDO_ST_DS_fl_p
with the following input table:
aaCDO_ST_DS_fl_p
|
Argument
|
Description
|
Example Data
|
Switch
|
|
d_v
|
Valuation date
|
1-Dec-2006
|
|
|
contra_d
|
CDS date table
|
see below
|
|
|
ref_bskt
|
Reference notional and recovery rate table
|
see example 7
|
|
|
tranche_type
|
Type of a tranche (or loss layer) definition
|
1
|
Proportional
|
|
tranche_corr
|
Tranche table
|
see below
|
|
|
corr_type
|
Correlation type
|
1
|
tranche correlation
|
|
freq_pr
|
Premium payment frequency
|
3
|
Quarterly
|
|
acc
|
Accrual method
|
2
|
act./360
|
|
d_rul
|
Business day convention, a switch.
|
2
|
next business day
|
|
modl_type
|
Model type
|
1
|
normal copula
|
|
modl_para
|
Model parameter table
|
see above
|
|
|
dp_type
|
Default curve type
|
1
|
par CDS spread curve
|
|
dp_bskt
|
Par CDS spread curve
|
see example 6
|
|
|
intrp_tb
|
Default curve parameter table
|
see example 1
|
|
|
hl
|
A holiday list
|
0
|
|
|
dfstd
|
The discount factor curve
|
|
|
|
intrp
|
Interpolation method of the discount factor curve, a
switch.
|
1
|
|
|
accu_level
|
Level of accuracy
|
2
|
accuracy level 2
|
|
calc_para
|
Calculation parameter table
|
see above
|
|
|
stat
|
Stat list
|
{1, 2,…,23}
|
|
|
tranche_list
|
Tranche list
|
1, 2
|
|
Tranche Table
|
Attachment
|
Detachment
|
Notional
|
Coupon
|
Position
|
Notional adjustment method
|
Upfront fee
|
|
0
|
0.1
|
0
|
0.05
|
1
|
1
|
0.3
|
|
0.1
|
0.2
|
0
|
0.02
|
2
|
1
|
0.1
|
|
0.2
|
0.3
|
0
|
0
|
1
|
1
|
0
|
Results
|
Output Statistics
|
Description
|
Tranche 1
|
Tranche 2
|
|
1
|
Fair value
|
782977.281
|
-352400.7328
|
|
2
|
Value of payoff
|
1048989.81
|
-488908.6835
|
|
3
|
Value of premium
|
-266012.53
|
136507.9507
|
|
4
|
Accrued interest of premium
|
-20000
|
8000
|
|
5
|
Fair value minus accrued interest
|
802977.281
|
-360400.7328
|
|
6
|
Par spread
|
0.09125344
|
0.04496355
|
|
7
|
Ratio of par spread and reference credit spread aggregate
|
0.35097478
|
0.172936731
|
|
8
|
Attachment point
|
0
|
2000000
|
|
9
|
Detachment point
|
2000000
|
4000000
|
|
10
|
Tranche size
|
2000000
|
2000000
|
|
11
|
Tranche notional
|
2000000
|
2000000
|
|
12
|
Tranche loss up to the valuation date, inclusive
|
0
|
0
|
|
13
|
Outstanding tranche notional
|
2000000
|
2000000
|
|
14
|
DVOX of credit default spreads
|
2675.09
|
-2109.10
|
|
15
|
Rho
of recovery rate
|
6342.18
|
2393.29
|
|
16
|
Rho
of correlations or factor loading
|
-92586.93
|
520.43
|
|
17
|
BPV of risk-free rate
|
-130.48
|
81.37
|
|
18
|
Theta
|
-548.46
|
379.61
|
|
19
|
Number of days that premium accrues
|
72
|
72
|
|
20
|
Next coupon date
|
20-Dec-06
|
20-Dec-06
|
|
21
|
Previous coupon date
|
20-Sep-06
|
20-Sep-06
|
|
22
|
Number of remaining cash flows
|
17
|
17
|
|
23
|
Implied upfront fee given premium coupon
|
0.40148864
|
0.180200366
|
Example 9: Deltas with
respect to the CDS spreads of individual entities
Suppose in example 8 we want to calculate the deltas of
name 1 and name 2. Then we should use
the function aaCDO_ST_DS_risk.
Its input table is similar to that of aaCDO_ST_DS_p
except that it has an output type parameter and a name list table and has no
statistics list. For this example, the output type is 1 (delta) and the entity
list is {1, 2}. The following are the
outputs:
Output Table Results
|
Name
|
Tranche 1
|
Tranche 2
|
|
1
|
-0.42511
|
0.290643661
|
|
2
|
-0.38811
|
0.300931327
|
From the above table we see that to hedge the equity
tranche the trader should sell CDS of both name 1 and name 2, and to hedge
tranche 2 the holder of the tranche portfolio should buy CDSs of the names. The
net hedge will be to sell CDSs of name 1 and name 2 with notionals of:

and
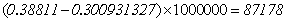
respectively.
Example 10: Bespoke tranches
To value bespoke tranches of synthetic credit risk, one
often makes the standardized tranches, such as tranches of iTraxx
or Dow Jones CDX,
benchmarks for calibrating credit models. Function aaCDO_std_baseCorr_map
can be used to calibrate base correlations of bespoke tranches. Suppose that the
reference pool and base correlations of a benchmark CDO are given as follows:
Benchmark references table
|
notional of an entity
|
recovery rate
|
number of entities
|
|
100
|
40.000%
|
3
|
Benchmark basket default probability curve
|
time in years
|
default probability of entity 1
|
default probability of entity 2
|
default probability of entity 3
|
|
1
|
0.022032
|
0.0317
|
0.0219
|
|
2
|
0.046242
|
0.0655
|
0.0461
|
|
3
|
0.07266
|
0.1022
|
0.0725
|
|
4
|
0.101233
|
0.142
|
0.101
|
|
5
|
0.131885
|
0.1752
|
0.1315
|
Benchmark base correlation table
|
detachment point
|
base correlation
|
|
0.03
|
0.07
|
|
0.07
|
0.11
|
|
0.15
|
0.15
|
Also suppose that reference pool and tranche
detachment points of the bespoke CDO are described in the following tables:
Bespoke reference table
|
notional amount
|
recovery rate
|
|
100
|
0.3
|
|
200
|
0.4
|
|
300
|
0.4
|
Bespoke basket default probability curve
|
time in years
|
default probability of entity 1
|
default probability of entity 2
|
default probability of entity 3
|
|
1
|
0.022032
|
0.0317
|
0.0219
|
|
2
|
0.046242
|
0.0655
|
0.0461
|
|
3
|
0.07266
|
0.1022
|
0.0725
|
|
4
|
0.101233
|
0.142
|
0.101
|
|
5
|
0.131885
|
0.1752
|
0.1315
|
Detachment points of bespoke tranches
|
detachment point
|
|
0.05
|
|
0.1
|
|
0.2
|
Input details are described in the following table:
aaCDO_ST_baseCorr_map
|
Argument
|
Description
|
Example Data
|
Switch
|
|
base_corr
|
benchmark base correlation table
|
See above
|
|
|
intrp_gen
|
base correlation interpolation method
|
1
|
linear
|
|
ref_bMark
|
benchmark references table
|
See above
|
|
|
ref_custom
|
bespoke references table
|
See above
|
|
|
prob_bMark
|
benchmark basket default probability curve
|
See above
|
|
|
prob_custom
|
bespoke basket default probability curve
|
See above
|
|
|
intrp_prob
|
interpolation method of probability curve
|
1
|
linear
|
|
time_m
|
time to maturity of CDO
|
2.5
|
|
|
detach_custom
|
detachment points of bespoke tranches
|
See above
|
|
|
map_type
|
mapping method of base correlations
|
1
|
match loss profiles
|
|
rescale
|
scaling factor (used when mapping type = 2 only)
|
100%
|
|
|
accu_level
|
level of accuracy
|
1
|
accuracy level 1
|
|
calc_method
|
calculation method
|
2
|
recursion method
|
Then the base correlations of the bespoke tranches
can be estimated by calling aaCDO_baseCorr_map:
Output table
|
detachment
point
|
base correlation
|
|
0.05
|
0.088824283
|
|
0.1
|
0.12196818
|
|
0.2
|
0.15
|
Example 11: Tranche loss distribution
The tranche value of a synthetic CDO is based on the
tranche loss distribution. Function aaCredit_tranche_loss_prob_cum
can be used to calculate the tranche loss distribution. Suppose, in Example 10,
one likes to know the loss distribution of the bespoke equity tranche. To use
this function, we specify the following inputs:
aaCredit_tranche_loss_prob_cum
|
Argument
|
Description
|
Example Data
|
Switch
|
|
ref_bskt
|
notional and recovery rate table
|
see above
|
|
|
prob_bskt
|
default probability curve
|
see below
|
|
|
intrp_prob
|
interpolation method of probability curve
|
1
|
linear
|
|
tranche_bound
|
tranche and loss range table
|
see below
|
|
|
tranche_type
|
type of tranche definition
|
1
|
tranche boundaries are proportional to the total
notional
|
|
modl_type
|
model type
|
1
|
normal copula
|
|
modl_para
|
model parameters
|
see below
|
|
|
time_points
|
time points (in years) at which loss probabilities
are to be calculated
|
see below
|
|
|
accu_level
|
level of accuracy
|
1
|
accuracy level 1
|
|
calc_method
|
calculation method
|
2
|
recursion method
|
|
output_type
|
output type
|
1
|
tranche loss distribution
|
Tranche and loss range table
|
attachment point
|
detachment point
|
lower loss bound
|
upper loss bound
|
|
0
|
0.05
|
0
|
0.05
|
Time points (in years) at which loss probabilities are to
be calculated
|
time length
(in years)
|
|
0.5
|
|
1
|
|
5
|
 Note that the factor loading is the square root
of the correlation.
Note that the factor loading is the square root
of the correlation.
Model parameters
|
factor loading
|
|
0.298034029690451
|
Calling aaCredit_tranche_loss_prob_cum,
we get the following loss distributions for the equity tranche:
Output table
|
attachment point
|
detachment point
|
probability of loss from time 0
to time point 1
|
probability of loss from time 0
to time point 2
|
probability of loss from time 0
to time point N
|
|
0
|
0.05
|
0.0370100730996259
|
0.0727404397902457
|
0.297664746815289
|
References
[1]
Andersen, L. Sidenius, J. and Basu, S. (November
2003), ‘All your hedges in one basket,’ Risk,
67-72.
[2]
Andersen L., Sidenius, J. et al, (2004), The Bank of America Guide to Advanced Correlation
Products, Incisive Financial Publishing.
[3]
Brasch, H. (2004), ‘A note on efficient pricing
and risk calculation of credit basket products’, TD Securities.
[4]
Burtschell, X., Gregory, J. and Laurrent, J.,
(2005), A Comparative Analysis of CDO Pricing models,
preprint.
[5]
Debuysscher, A. and Szego, M., (2003), The Fourier Transform Method – Technical document,
Moody’s Investors Service.
[6]
Fabozzi, F. and Goodman, L., (2001), Investing in Collateralized Debt Obligations, New Hope, J. Fabozzi
Associates.
[7]
Luo L., (May 2006), ‘CDOs and Search for Simplicity’,
Wilmott Magazine,
[8]
Merrill Lynch, (June 2004), ‘Standardized
Tranches’, Credit Derivatives Research.
[9]
McGinty, L., Beinstern, E. and Watts, M., (2004), Credit
Correlation, A Guide, JP Morgan publication.
[10]
Pugachevsky, D. (2005), ‘How to value bespoke
synthetic CDO tranches consistent with standard ones’, preprint.
[11] Schonbucher,
P., (2003), Credit Derivatives Pricing, Models,
Pricing and Implementation, Wiley Finance.
Disclaimer
With respect to this document,
FinancialCAD Corporation (“FINCAD”) makes no warranty either express or
implied, including, but not limited to, any implied warranty of merchantability
or fitness for a particular purpose. In no event shall FINCAD be liable to
anyone for special, collateral, incidental, or consequential damages in
connection with or arising out of the use of this document or the information
contained in it. This document should not be relied on as a substitute for your
own independent research or the advice of your professional financial,
accounting or other advisors.
This information is subject to
change without notice. FINCAD assumes no responsibility for any errors in this
document or their consequences and reserves the right to make changes to this
document without notice.
Copyright
Copyright © FinancialCAD
Corporation 2008. All rights reserved.
![]()
![]() , respectively. Let
, respectively. Let ![]() denote the accumulated
loss of the pool at time
denote the accumulated
loss of the pool at time ![]() (the current time is 0).
Let
(the current time is 0).
Let ![]() denote the (full) notional
of the tranche at time
denote the (full) notional
of the tranche at time![]() . Then:
. Then:![]()
![]() be the time
be the time ![]() value of the premium leg (also called a fixed leg or a fee
leg) of a credit default swap on the tranche. Let
value of the premium leg (also called a fixed leg or a fee
leg) of a credit default swap on the tranche. Let ![]() be the annual premium
coupon rate and
be the annual premium
coupon rate and ![]() the premium coupon
payment time points. The premium payment amount at a premium payment date is
the product of the premium rate and the current notional of the tranche. For
most synthetic CDO deals, when an entity defaults prior to payment date, the
accrued interest must be paid at the default time. For other less common
synthetic CDOs there is no such accrued premium payment. Accordingly, the
present value of the premium payments can be calculated as
the premium coupon
payment time points. The premium payment amount at a premium payment date is
the product of the premium rate and the current notional of the tranche. For
most synthetic CDO deals, when an entity defaults prior to payment date, the
accrued interest must be paid at the default time. For other less common
synthetic CDOs there is no such accrued premium payment. Accordingly, the
present value of the premium payments can be calculated as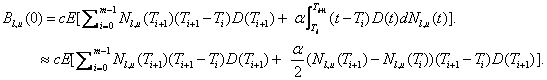
![]() is a risk-free
discount factor curve and the constant
is a risk-free
discount factor curve and the constant ![]() if the accrued premium
is paid when an entity defaults prior to a premium payment date; and
if the accrued premium
is paid when an entity defaults prior to a premium payment date; and ![]() , otherwise.
, otherwise.![]() be the time t value of
the payoff leg (also called a default leg or a floating leg or an asset leg) of
the CDS. Then:
be the time t value of
the payoff leg (also called a default leg or a floating leg or an asset leg) of
the CDS. Then:![]()
![]()
![]()