Interest Rate Curve Generation
Overview
FINCAD Zero Coupon Curves
Bootstrapping a set of quoted benchmark rates and security
prices creates zero coupon discount factor curves. Bootstrapping starts with the shortest term
security and steps through them all in ascending order of maturity. At every step, discount factors from the
preceding securities are used to determine the discount factor for the current
one. The curve generation process strips
each security into its individual cashflows and then prices it using zero
coupon pricing.
A zero curve is the most basic requirement for pricing and
hedging interest rate (and many other) derivatives and FINCAD XL offers a suite
of functions for:
·
Bootstrapping money market and futures rates
·
Bootstrapping swap market curves, for example
the LIBOR curve, based on market quoted money market rates, FRA or futures
rates and swap rates
·
Bootstrapping bond market curves, for example
the treasury curve, based on market quoted money market rates, FRA or futures
rates and bond prices
·
Manipulating (adding spreads, extending,
smoothing) interest rate curves
Formulas & Technical Details
Choosing benchmark instruments for input is an important
part of the curve generation process.
The underlying benchmark interest rate securities may be money market
instruments (such as T-bills, LIBOR deposit, etc.), FRA's (forward rate
agreements), interest rate futures (such as Eurodollar futures), government
bonds or quoted par swap rates.
Liquidity, risk rating of the instrument being valued and availability
of quotes are taken into consideration when making the choice. Generally, the process will involve more than
one type of instrument in order to cover the entire range of maturities that
accurately describe the term structure of interest rates.
Benchmark quotes that are selected for the curve are fed
into the function in the form of tables.
Each table contains a row per quote.
Every row has fields that help describe the benchmark rate or security
represented by the quote. What follows
is a description of these tables and some sample tables that are used as
examples in the outline of the bootstrapping process.
Note: The tables shown in this document were
designed as sample inputs for a curve as of 27 May 1998. The “Use?” field in the tables specifies
whether the rate should be used in the curve generation or not.
Each rate is described using a settlement (or effective)
date, maturity date, accrual method (e.g. act/360) and a compounding method
(e.g. simple interest). These fields are
input in the form of a table, an example of which is displayed below. Any adjustment for holidays or weekends or
settlement days is done prior to the curve building (see the Bond Curve and Swap
Curve workbook in FINCAD XL). Note that
the rate compounding method and the accrual method may be set differently for
individual rates.
|
Effective Date
|
Maturity Date
|
Rate
|
Compounding
|
Accrual
|
Use?
(Y = 1, N = 0)
|
|
28-May-1998
|
29-May-1998
|
5.26%
|
7
|
2
|
1
|
|
29-May-1998
|
01-Jun-1998
|
5.26%
|
7
|
2
|
0
|
|
29-May-1998
|
05-Jun-1998
|
5.32%
|
7
|
2
|
0
|
|
29-May-1998
|
30-Nov-1998
|
5.47%
|
7
|
2
|
0
|
|
29-May-1998
|
26-Feb-1999
|
5.54%
|
7
|
2
|
1
|
|
29-May-1998
|
28-May-1999
|
5.60%
|
7
|
2
|
0
|
Each of these rates is defined using an effective date,
maturity date, quoted rate, accrual method (e.g. act/360) and a compounding
method (e.g. simple interest). The
settlement date, maturity date, quoted rate, rate accrual method and rate
compounding method are inputs to the curve functions in a table of the form
displayed below. Any adjustment to the
settlement and maturity dates is done prior to the curve building (see the Bond
Curve and Swap Curve workbook in FINCAD XL).
Note that the rate compounding method and accrual method may be set
differently for individual rates.
|
Contract*
|
Effective Date
|
Maturity Date
|
Rate
|
Compounding
|
Accrual
|
Use?
(Y = 1, N = 0)
|
|
Jun-1998
|
17-Jun-1998 Wed
|
15-Sep-1998 Tue
|
0.000%
|
7
|
2
|
0
|
|
Jul-1998
|
15-Jul-1998 Wed
|
13-Oct-1998 Tue
|
0.000%
|
7
|
2
|
0
|
|
Aug-1998
|
19-Aug-1998 Wed
|
17-Nov-1998 Tue
|
0.000%
|
7
|
2
|
0
|
|
Sep-1998
|
16-Sep-1998 Wed
|
15-Dec-1998 Tue
|
0.000%
|
7
|
2
|
0
|
|
Dec-1998
|
16-Dec-1998 Wed
|
16-Mar-1999 Tue
|
0.000%
|
7
|
2
|
0
|
|
Mar-1999
|
17-Mar-1999 Wed
|
15-Jun-1999 Tue
|
6.000%
|
7
|
2
|
1
|
|
Jun-1999
|
16-Jun-1999 Wed
|
14-Sep-1999 Tue
|
6.010%
|
7
|
2
|
1
|
|
Sep-1999
|
15-Sep-1999 Wed
|
14-Dec-1999 Tue
|
6.020%
|
7
|
2
|
1
|
|
Mar-2008
|
19-Mar-2008 Wed
|
17-Jun-2008 Tue
|
0.000%
|
7
|
2
|
0
|
*The Contract field is not
part of the input.
To correctly specify the par swap rate inputs, the user
has to define the coupon frequency, the date adjustment rule and the accrual
method for every rate, as shown in the table below:
|
Effective Date
|
Maturity Date
|
Rate
|
Fixed Leg Frequency
|
Fixed Leg Accrual
|
Date Adj. Rule
|
Use?
(Y = 1, N = 0)
|
|
29-May-1998
|
29-May-1999
|
0.000%
|
1 (= annual)
|
2 (= act/360)
|
1 (= no adj.)
|
0
|
|
29-May-1998
|
29-May-2000
|
5.702%
|
1
|
2
|
1
|
0
|
|
29-May-1998
|
29-May-2001
|
5.731%
|
1
|
2
|
1
|
1
|
|
29-May-1998
|
29-May-2002
|
5.764%
|
1
|
2
|
1
|
0
|
|
29-May-1998
|
29-May-2003
|
5.780%
|
1
|
2
|
1
|
1
|
|
29-May-1998
|
29-May-2028
|
0.000%
|
1
|
2
|
1
|
0
|
Coupon dates for every par swap are generated
from the maturity date supplied by the user as part of the rate
definition. All coupon dates including
the maturity date are adjusted for holidays and weekends internally in the
manner specified by the user in the date adjustment rule field.
Therefore the maturity dates that are input into the table
above should be cycle dates for correct usage of the curve generation
procedure.
In some cases, e.g. trading the afternoon swap curve in
some jurisdictions, it may be that the first reset
rate of the floating leg of the underlying swap has been set. This situation is handled by optionally
adding an 8th column to the par swap table.
Furthermore, if a reset rate is given in the 8th column, then the frequency
and accrual method of the floating leg matters (If the first reset has not been set,
then the frequency and accrual method of the floating leg are irrelevant since
the floating leg values to par). It is
possible to specify the frequency and accrual method of the floating leg in the
9th and 10th columns respectively of the par swap table. These columns are optional. If the frequency of the floating leg is not
provided in the 9th column then it is assumed to be the same as that of the
fixed leg. If the accrual method of the
floating leg is not provided in the 10th column then it is assumed to be the
same as that of the fixed leg.
The attributes required for defining a bond for input to
the curve functions are:
·
Frequency: refers to the coupon frequency of
the bond (See appendix for settings allowed)
·
Settlement date: is the date on which the
clean price (and accrued interest) are exchanged.
·
Effective date (or dated date): is the date on
which the bond began to accrue interest The effective date should only be set
if the bond has yet to start accruing interest (a new issue) or if the bond has
been issued but is in an odd first coupon period (when using aaBond_crv2(),
otherwise it can be set to 0.
·
Clean price: is the price of the bond, per 100
notional, not including accrued interest. This price is as of settle date.
·
Accrued interest: is the accrued interest, per
100 notional as of the settle date.
Note: If
the accrued interest is less than zero, the bond is assumed to be ex-dividend and all calculations will be adjusted accordingly.
·
Cashflow adjustment: allows the bond payment
dates to be adjusted for weekends and holidays.
·
First coupon date: only required if the first
coupon period for the bond is odd. If
the first coupon period is a regular period, this input can be set to 0.
·
Last coupon date prior to maturity: is the
date of the next to last coupon payment.
If the bond has a regular last coupon period this input can be set to 0.
·
Accrual method: the accrual method for
calculating the coupon amount in either an odd-first and / or an odd-last
coupon period. It does not effect any
other periods and the bonds are assumed to make level coupon payments.
The Bootstrapping Process
Each of these rates can be described using a settlement
date, maturity date, and a rate (with basis, accrual method). The user sets the interpolation method
(either from discount factors or from spot rates). We note that the bootstrapping of these
short-term rates is done the same in all of the various curve building
functions whether it be for swaps, bonds or average-rate swaps.
Main ideas
1. Rates
are organized from shortest maturity date to longest maturity date (only the
rates marked for “use in the curve” are used while the other rates are
ignored). The bootstrapping process then iterates through this list of rates
with ascending maturity, and calculates discount factors for all the maturity
dates. At the same time, a spot rate is also calculated for each of these
discount factors.
2. For
any rate with settlement date = value date, calculation of a discount factor is
straightforward. Discount factors are
first calculated for all rates that settle on the value date. Generally these are some of the money market
rates. The calculation for these discount factors is of the form:
,
where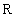 
is a simple interest
rate, and the value of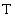 
(time in years)
depends on the accrual method of the specified rate.
3. All rates
that do not settle on the value date are treated as forward rates. The discount factor calculation for these
rates involves an extra step as compared to those in Step 2. A discount factor for the settlement date of
every forward rate is required. Based on
the bootstrapping setting, the discount factor is either interpolated linearly
from previous discount factors (described as "interpolate from discount
factors") or its spot rate is linearly interpolated from previous spot
rates, and then the
discount factor is calculated from this spot rate. The calculation is of the form:
.
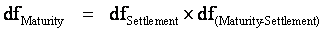Note: If
the curve is going to be built with swap rates or bond prices, any money market
or futures rates whose maturity date is beyond the first swap rate (or first
bond) will not be used.
The aim of this part of the process is to back out a
discount factor for each grid date, from the swap rate data available. The grid dates are the same as the coupon
dates for the swaps and are dependant on the swap definitions specified in the
input tables. The bootstrapping process
iterates through the par swap rates, using the rules stated below, and outputs
discount factors and spot rates for all grid dates that are greater than the
last date in the curve to this point.
Related to swap rates, five basic bootstrapping methods are available,
as follows:
1.
Linear Par Swap Rates
A linear par swap rate profile is assumed from the
previous par swaps maturity date to the current swaps maturity date. Given the par swap rate at a coupon date, the
discount factor (and spot rate) at each coupon date can be calculated.
e.g.: From the sample tables, if we were only using
the par swap rate for 29th May 2001 followed by the rate for 29th May 2003,
this step would first linearly interpolate a par swap rate for 29th May 2002. This would come out to (5.7800 + 5.7310) / 2 =
5.7555. This rate is used to calculate the discount factor for the grid point
29th May 2002. The next step is to use
the resulting curve for generating the 29th May 2003 discount factor (as
explained in Section 3).
2.
Constant Implied Forwards
In this case, it is assumed that the forward rate between each of the remaining coupons is constant. This
constant forward rate is solved for using in iterative procedure subject to the
condition of obtaining the correct par swap rate at the first par swap
date. The discount factor, at each
coupon date greater than the end of the prior curve, is output by the curve
generator.
e.g.: For the above example, we assume that the
implied forward rate between 29th May 2001 and 29th May 2002 is the same as
that between 29th May 2002 and 29th May 2003.
Using this assumption, we calculate implied forward rate and use it to
generate the par swap rate for 29th May 2002, which is then used to calculate
the discount factor for 29th May 2002.
As above, the final step is to calculate the discount factor for 29th
May 2003 from the existing curve and the input par swap rate (as explained in
Section 3).
3. Linear
Implied Forwards (Original)
In this case, a first pass is made using the constant
implied forwards method. A second pass
at the curve bootstrapping is then made, assuming that the forward rates lie on
a series of line segments. The slope of
each line segment is chosen to ensure that the curve is consistent with the
input swap rates; i.e., we back out the correct swap rates from the curve. The segment is also chosen when it's possible
to slope with the direction of the forward rates; if the forward rates from the
first pass are increasing from one period to the next, the algorithm looks for
a straight line of positive slope.
However, if the forward rates from the first pass have a peak or a dip,
i.e., increasing then decreasing, or vice versa, then the algorithm assigns a
zero slope to that segment. A zero slope
is also assigned to the last segment.
The end result is a discount factor curve whose corresponding forward
rate curve is piecewise linear. The
forward rate curve is still not continuous; it is not possible to eliminate the
jumps altogether and preserve curve stability with the piecewise linear forwards
assumption. By curve stability, we mean
that the overall shape of the forward rate curve should not be hyper-sensitive
to small changes in the input swap rates.
4. Linear
Implied Forwards (Version 2)
This is the same as the original Linear Implied
Forwards method, except the algorithm has been refined so that it produces
smaller and fewer jumps (i.e., discontinuities) in the forward rate curve. For example, changes to the algorithm mean
that a steeper slope is allowed in each segment if this eliminates a
discontinuity with a neighboring segment.
The match points are calculated using the results of the first
pass. Another change is that the
algorithm assumes linear forwards during the tenor of the first swap if no cash
or futures rates are given, whereas the original method assumes constant
forward rates (zero slope) in this case.
The original Linear Implied Forwards method is retained for
compatibility with previous versions of FINCAD XL, or if an assumption of
constant forwards during the first swap is required when no cash or futures rates
are given.
5. Quadratic
Forwards
As above, a first pass is made using the constant
implied forwards methods. The quadratic
implied forwards algorithm then takes a second pass assuming that the forward
rates lie on a series of parabolic segments.
The parameters are chosen to ensure that the curve is consistent with
the input swap rates, and that the end points of each segment match those of
its neighbors. Again, the match points
are calculated using the results from the first pass. The end result is a discount factor curve
whose corresponding forward rate curve is piecewise quadratic and continuous (i.e.,
no jumps).
The aim of this part of the process is to extend (or
bootstrap) the discount factor curve to include each successive bond from the
given bond data table. The bonds that
are to be included in the input are first ordered from the shortest maturity to
the longest maturity. The bootstrapping
process then loops through the bonds, using the rules stated below, and outputs
discount factors and spot rates for all grid dates that are greater than the
last date in the curve based on data preceding the given bond. The deposit rate and futures rates are
bootstrapped as described above.
Splicing bonds into the curve
The bond under consideration is first stripped into its
component cashflows. A discount factor
is then interpolated for as many of these cashflow dates as possible. Discount factors for all the remaining
cashflow dates for this bond are calculated and output from the curve.
For bonds there are several possible bootstrapping
methods. They are based on whether
interpolation is done from discount factors or rates (as described above). They are also based on whether the
bootstrapping assumes constant forward rates between all of the
coupon dates, from the last coupon that the existing curve overlaps to the last
payment for the bond under consideration, or whether the bootstrapping assumes
a linear
forward rate profile (as described above for swaps). They are also based on whether an “enhanced”
curve with “all
points” is calculated.
Using a bootstrapping with “all points” will ensure that the resulting
discount factor curve will have a point for each coupon date of each bond that
was used to build the curve. This
ensures perfect roundtrip pricing for all of the bonds (but it will potentially
also lead to curves with many points).
Using Special Output Types
Key Rate Sensitivities
The aaSwap_crv3()
function can output key rate sensitivities. That is, it can output a number of
discount factor curves where each output curve is a result from bumping a raw
interest rate by a given spread. This is useful in risk analysis as it is used
to determine how sensitive a given portfolio is to changes in key interest
rates.
For example, suppose in the curve construction we are only
using money market (cash) and swap rates.
The money market (cash) curve table is using four rates, the futures
curve table is using five rates, and the swap curve table is using four
rates. The input spread for the curve
bump is 1basis point (assuming an additive bump). Then choosing the extended discount factor
curves as its table type, the output columns of aaSwap_crv3() will be:
|
dates
|
base curve
without any spreads applied
|
curve with spread
applied to every rate (i.e., a parallel shift)
|
curve with spread
applied to first raw rate in cash rates
|
curve with spread
applied to second raw rate in cash rates
|
…
|
curve with spread
applied to fourth raw rate in cash rates
|
curve with spread
applied to first raw rate in swap rates
|
…
|
curve with spread
applied to fourth raw rate in swap rates
|
Applying each of the discount factor curves to a portfolio
will determine how sensitive the portfolio is to changes in interest rates, so adjustments
can be made to the portfolio to achieve a desired risk profile.
Note: When
using this type of output in conjunction with extending the swap curve
(assuming the swap rates are being used) via the input "minimum length of
curve (in years)", the spread that is applied to the last used swap rate will
not be applied to the extended rate. For example, if we are given a spread of
1basis point (additive), the last given swap rate's maturity is ten years from
today at 5.00%, and the curve is to be extended from now to twelve years, the
last column of the output is a discount factor curve derived from a ten year
swap rate of 5.01%, and a twelve year swap rate of 5.00%.
FINCAD Functions
Swap Markets
aaSwap_crv(d_v,
cash_crv, fut_crv, swp_crv, method_boot, rate_basis, acc_rate, hl, method_gen)
The basic inputs are cash rates (in the table cash_crv),
futures or FRAs rates (in the table fut_crv) and par swap rates (in the table
swp_crv).
aaSwap_crv2(d_v,
cash_crv, fut_crv, swp_crv, method_boot, rate_basis, acc_rate, hl, method_gen, min_years,
sprd, sprdtype, table_type)
This is an extended version of aaSwap_crv. It is again based on the inputs of cash
rates, futures or FRA rates and par swap rates.
In addition, it allows the curve to be extended to a user specified
number of years (min_years). Further, a
spread may be specified. If the spread
type is absolute, (sprdtype = 1), the spread is added to all of the rates
building the curve. If the spread is
relative (sprdtype=2) each rate is scaled by this factor.
aaSwap_crv3(d_v,
cash_crv, fut_crv, swp_crv, boot_swap, boot_intrp, fut_splice, rate_basis,
acc_rate, hl, method_gen, min_years, extend_method, sprd, sprdtype, table_type)
This is essentially the same as aaSwap_crv2()
except that the bootstrap switch is broken into three switches: (a) swap
bootstrapping method (5 choices), (b) interpolation to use during bootstrapping
(3 choices), and (c) futures gap method (2 choices). The interpolation switch has an extra method,
which is “exponential from discount factors (log-linear)”, and the bootstrapping
method switch has two extra choices: “linear forward rates (v2)” and “quadratic
forward rates” (see below for explanation).
So aaSwap_crv3()
has 30 = 5x3x2 bootstrapping methods, whereas aaSwap_crv2()
has 12. In addition, aaSwap_crv3() can also output curve sensitivities
to a given spread on interest rates.
aaSimpleSwapCrv(d_v,
yield_crv, acc_mmkt, freq_swp, acc_swp, d_extend)
This is simplified version of aaSwap_crv(). It requires only one table (in the table
yield_crv) containing money market rates, if the maturity date is less than or
equal to one year, and swap rates otherwise.
The simplification does lead to less flexibility as there is no possibility
of entering any settlement periods (e.g. 2 market days on a rate) or using
futures rates. The bootstrapping method
used is constant implied forward rates, interpolate from discount factors.
A useful utility function is:
aaEDFut_CnvxAdj_HW(d_v,
d_e, d_t, vlt, a).
This function has one purpose. If one is building a swap curve and using
Eurodollar futures prices, it is necessary to adjust the rates by a convexity adjustment.
This function calculates a convexity adjustment based on either
the Ho-Lee or the Hull-White term structure model using the volatility, vlt, and the mean reversion, a, related to these models. These
parameters can be calibrated with the aaCalibrate*
family of functions or calibration workbooks in FINCAD XL.
Bond Markets
aaBond_crv1(d_v,
cash_crv, fut_crv, bond_crv, method_boot, rate_basis, acc_rate, hl, method_gen)
aaBond_crv2(d_v,
cash_crv, fut_crv, bond_crv, method_boot, rate_basis, acc_rate, hl, method_gen)
The basic inputs are cash rates (in the table cash_crv),
futures or FRAs rates (in the table fut_crv) and quoted bond prices (in the
table bond_crv). The bonds may be of any frequency (annual, semi-annual,
quarterly or monthly) and may be cum or ex-dividend. This essentially covers (almost) any level
coupon bonds (e.g., US Treasuries, Gilts, Bunds, French OATs, Corporates,
Municipals, etc.). The function aaBond_crv1()
works for regularly dated bonds (i.e., no odd dates), while aaBond_crv2()
is slightly more general in that it allows the possibility of
bonds with odd first and / or odd last coupon periods.
The function aaBond_crvJGB() is
specifically designed to work with Japanese government bonds (JGBs)
aaBond_crvJGB
(d_v,
cash_crv, fut_crv, bond_crv, method_boot, rate_basis, acc_rate, hl, method_gen )
US
Municipal and Tax-Exempt Markets
aaSwap_crv_avg(d_v,
cash_crv, swapcrv_bma_tbl, freq_fixed, drul_fix, acc_fix, freq_fl, drul_fl, acc_flt,
d_reset_cycle, reset_freq, d_rul_reset, acc_rt, reset_mktdays, rate_reset, hl, df_crv_disc,
intrp, rate_use, method_boot, output_type)
Though the function is general in design, the main
application is for the US Municipal and tax-exempt markets. For example, this function calculates a BMA
curve, where the underlying swaps are average rate swaps, where the coupons are
calculated based on the average of weekly resets. Another feature is that the coupons are
discounted at another rate, which in the BMA case is LIBOR. See the Tax-Exempt
(Municipal) Swap Curve FINCAD Math Reference document for more details.
Utilities
A more detailed description of these functions is
available in the Interest Rate Curve Utilities
FINCAD Math Reference document.
aaDFCurve_SmoothFwdRate(df_crv,
freq, d_e, d_t, meth_smooth)
This is a useful utility that will add points to the input
discount factor in such a way as to ensure smooth forward rates. For example, after bootstrapping a swap curve
built from annual swap rates, there will be parts of the curve with one year
gaps between points. By setting the
frequency to, e.g., quarterly (freq=3), in these gaps, quarterly discount
factors are calculated. The discount
factors are calculated in such a way as to ensure a smooth progression of
quarterly forward rates. The original
curve points remain unchanged.
aaDFCurve_SmoothFwdRate2(df_crv,
freq, d_e, d_t, meth_smooth, rate_basis, acc_rate, table_type)
This function is the same as aaDFCurve_SmoothFwdRate,
except that it can also include spot rates in the output table, depending on
the table_type input.
aaDFCurve_Extend(df_crv,
min_years)
This function takes an existing discount factor curve and
extends it to at least min_years years. The extension is calculated by assuming the
annualized par swap at min_years (annual, act/365) is equal to the longest
available par swap rate that can be calculated from the df_crv. If min_years is less than the length of the
original curve, no extension is done.
The curve is only extended while the original curve points remain
unchanged.
aaDFCurve_AddSpread(df_crv,
min_years, rate_basis_mgn, acc_mgn, sprd_type, sprd_yield)
aaDFCurve_AddSpreads(df_crv,
min_years, rate_basis_mgn, acc_mgn, sprd_type, sprd_tbl)
These functions add a spread, or a term structure of
spreads, to an existing discount factor curve.
If the spread type is absolute (sprd_type = 1), the relevant spread is
added to the implied spot rate for each point in the discount factor curve. If the spread type is relative (sprd_type =
2), the implied spot rates are scaled by the factor spread (i.e. rate_new =
rate_original 
spread. The spread functions will also extend the
underlying curve if desired (using aaDFCurve_Extend).
Disclaimer
With respect to this document,
FinancialCAD Corporation (“FINCAD”) makes no warranty either express or
implied, including, but not limited to, any implied warranty of merchantability
or fitness for a particular purpose. In no event shall FINCAD be liable to
anyone for special, collateral, incidental, or consequential damages in
connection with or arising out of the use of this document or the information
contained in it. This document should not be relied on as a substitute for your
own independent research or the advice of your professional financial,
accounting or other advisors.
This information is subject to change
without notice. FINCAD assumes no responsibility for any errors in this
document or their consequences and reserves the right to make changes to this
document without notice.
Copyright
Copyright © FinancialCAD Corporation 2008.
All rights reserved.