Quanto Forwards and Options

Overview

Quantos are best described through an example. Consider the Nikkei index 225 Stock Average, which is, of course, measured in yen. A quanto of the Nikkei index is a new entity which we define to be the value of the index measured in US dollars. In more detail, if the index on a certain day has a value of ¥18000, this number is treated as $18000, instead of ¥18000. In practice, this number is often multiplied by a constant, which is considered as a fixed FX rate.

To value a derivative based on a quanto one must take into consideration the FX rate. Hence there are two sources of risk and a two factor model must be used. This is the basic difference between derivatives on quantos and those on non-quanto underlyings as described in the following section.

Formulas & Technical Details

We give a brief and simple description on valuing quanto forwards and options. Detailed and rigorous mathematical derivation can be found in the book of Baxter and Rennie [1]. The valuation of quanto forwards is also dealt with in Hull [2].

For clarity we use the Japanese stock index, Nikkei 225 Stock Average, to describe the valuation of quanto forwards and options. Define:

: Nikkei index measured in yen at time

: FX rate: dollar value per unit of yen.

: dividend yield on the Nikkei index

: domestic ($) risk-free rate

: risk-free rate of the Japanese yen.

As in the Black-Scholes model, and are assumed to follow lognormal distributions and the rates , and are assumed to be constant during the life of a forward contract or an option on the index.

As a quanto, the Nikkei index has a price of measured in US dollars. The variable involves two sources of risk: the risk associated with the index and the risk associated with the FX rate. It can be shown that this quanto is not tradable in the US dollar market. In order to value quanto derivatives one needs to construct a “risk-neutral” probability measure under which both the risk of FX rate and the risk of the underlying are “risk-neutral” (i.e., both the two stochastic processes and are martingales with respect to this probability measure). It can be proven that such a measure exists and is unique. Let denote this probability measure. We can then write down the forward price of the above quanto and the fair values of European style call and put and binary options as follows.

Forwards

Let be the delivery price of a forward contract on the Nikkei index. Then it can be shown that, eliminating arbitrage opportunities,

where

and are the annualized volatilities of the Nikkei index and the FX rate , respectively, and

is the correlation of log and log

European Style Call and Put Options

Let be the strike price of a European style call option on the Nikkei index. Then the fair value of a call option on the index is given by

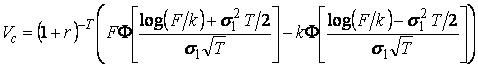
Binary (Digital) Options

A binary option has, at expiry, a payoff of a fixed amount (or the asset itself) or nothing depending on whether the underlying asset is above or below a strike level.

1. Cash or nothing call

where is the cash payment at the expiry.

2. Cash or nothing put

3. Asset or nothing call

4. Asset or nothing put

FINCAD Functions

Quanto Forwards

aaQuanto_fwd(price_ufor, FX_fix, d_exp, d_v, vlt_u, vlt_FX, corr, rate_for, cost_hldg, stat):

Calculates the forward price and risk statistics of a quanto asset.

Quanto Options

The following functions return the fair value and risk statistics for the quanto version of different types of options (Please refer to corresponding documents for different types of options for more information):

aaQuanto_Asian(price_ufor, ex_for, FX_fix, average, sam_freq, d_exp, d_v, d_aver, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, option_type, stat)

aaQuanto_asian_basket_fs_MC(asian_bskt_info, ex, curr_tbl, corr_matrix, d_v, d_exp, d_aver, sam_seq, option_type, num_rnd, table_type)

aaQuanto_asian_basket_MC(asian_bskt_info, ex, curr_tbl, corr_matrix ,d_v, d_exp, d_aver, sam_freq, option_type, num_rnd, table_type)

aaQuanto_Barrier_am(price_ufor, ex_for, FX_fix, bar, d_v, d_exp, bar_type, rebate, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, option_type, optimize, stat)

aaQuanto_Barrier_dbl(d_v, d_exp, price_ufor, ex_for, FX_fix, bar1, bar2, rebate_up, rebate_dn, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, option_type, optimize, option_style, stat)

aaQuanto_Barrier_dbl_bin(d_v, d_exp, price_ufor, ex_for, FX_fix, bar1, bar2, rebate_exp, rebate_up, rebate_dn, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, option_type, optimize, stat)

aaQuanto_Barrier_eu(price_ufor, ex_for, FX_fix, bar, d_v, d_exp, bar_type, rebate, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, option_type, stat)

aaQuanto_basket_MC(bskt_info, ex, curr_tbl, corr_matrix, d_v, d_exp, option_type, num_rnd, table_type)

aaQuanto_Berm(price_ufor, ex_for, FX_fix, d_exp, d_v, d_berm_list, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, option_type, iter, stat)

aaQuanto_BIN2(price_ufor, ex_for, FX_fix, d_exp, d_v, vlt_u, vlt_FX,corr, rate_for, rate_dom, cost_hldg, option_type, iter, stat)

aaQuanto_bin_cash(price_ufor, ex_for, d_exp, d_v, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, div_yield, cash, option_type, stat)

aaQuanto_bin_asset(price_ufor, strk_level, FX_fix, d_exp, d_v, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, div_yield, option_type, stat)

aaQuanto_Binary_hit_asset(price_ufor, bar, FX_fix, d_v, d_exp, bar_type, paytime_type, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, stat)

aaQuanto_Binary_hit_cash(price_ufor, bar, FX_fix, d_v, d_exp, bar_type, cash, paytime_type, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, stat)

aaQuanto_Binary_in_asset(price_ufor, ex_for, FX_fix, bar, d_v, d_exp, bar_type, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, option_type, stat)

aaQuanto_Binary_in_cash(price_ufor, ex_for, FX_fix, bar, d_v, d_exp, bar_type, cash, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, option_type, stat)

aaQuanto_Binary_nohit_asset(price_ufor, bar, FX_fix, d_v, d_exp, bar_type, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, stat)

aaQuanto_Binary_nohit_cash(price_ufor, bar, FX_fix, d_v, d_exp, bar_type, cash, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, stat)

aaQuanto_Binary_out_asset(price_ufor, ex_for, FX_fix, bar, d_v, d_exp, bar_type, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, option_type, stat)

aaQuanto_Binary_out_cash(price_ufor, ex_for, FX_fix, bar, d_v, d_exp, bar_type, cash, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, option_type, stat)

aaQuanto_Chooser(d_v, d_exp_opt, price_ufor, d_exp_call, ex_call, d_exp_put, ex_put, FX_fix, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, stat)

aaQuanto_Compound(d_v, d_exp_opt, option_type_c, ex_cmpd, d_exp_u, price_ufor, ex_u, FX_fix, option_type_u, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, stat)

aaQuanto_FSopt(d_v, d_issue, d_exp, price_ufor, ex_scaling, FX_fix, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, option_type, stat)

aaQuanto_fwd(price_ufor, FX_fix, d_exp, d_v, vlt_u, vlt_FX, corr, rate_for, cost_hldg, stat)

aaQuanto_Geo_Asian(price_ufor, ex_for, FX_fix, d_v, d_exp, d_aver, average, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, sam_freq, option_type, stat)

aaQuanto_Geo_Asian_fs(price_ufor, ex_for, FX_fix, d_v, d_exp, d_aver, average, vlt_u, vlt_FX, corr,rate_for_ann, rate_dom_ann, cost_hldg, sam_seq, option_type, stat)

aaQuanto_Geo_aver_strk(price_ufor, FX_fix, d_v, d_exp, d_aver, average, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, sam_freq, option_type, stat)

aaQuanto_Geo_aver_strk_fs(price_ufor, FX_fix, d_v, d_exp, d_aver, average, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, sam_seq, option_type, stat)

aaQuanto_Look(price_ufor, ex_for, FX_fix, d_v, d_exp, vlt_u, vlt_FX, corr, rate_for_ann, rate_dom_ann, cost_hldg, option_type, stat)

aaQuanto_opt(price_ufor, ex_for, FX_fix, d_exp, d_v, vlt_u, vlt_FX, corr, rate_for, rate_dom, cost_hldg, option_type, stat)

Root Finding Functions for Quantos

Many of these FINCAD functions have their inverse (root finding) versions:

aaQuanto_Barrier_am_ix

aaQuanto_Barrier_dbl_ix

aaQuanto_Barrier_dbl_bin_ix

aaQuanto_Barrier_eu_ix

aaQuanto_Binary_hit_asset_ix

aaQuanto_Binary_hit_cash_cash

aaQuanto_Binary_in_asset_ix

aaQuanto_Binary_in_cash_ix

aaQuanto_Binary_nohit_asset_ix

aaQuanto_Binary_nohit_cash_ix

aaQuanto_Binary_out_asset_ix

aaQuanto_Binary_out_cash_ix

These “_ix” (implied x, where x is any input parameter) functions find the value of any input parameter for a given value of an output statistic. More details can be found in the General Root Finding (_ix) Functions FINCAD Math Reference document.

Description of Inputs

Input Argument	Description
FX_fix	A positive constant
d_exp	Expiry date of the option.
d_v	Value date
vlt_u	The annualized volatility of the underlying (foreign) asset.
vlt_FX	The annualized volatility of the FX rate.
corr	The correlation between the return of the underlying and that of the FX rate. See details in the last section.
rate_dom rate_for div_yield	These rates are quoted on an annually compounded, Act / 365 (fixed) basis. The parameter rate_dom is the relevant domestic risk-free interest rate, rate_for is the relevant foreign risk-free rate, and div_yield the dividend payout rate of the underlying (foreign) asset
stat	See the description of the output in the examples below.
ex	Strike price of an option.
cash	The payoff at the expiration of a binary option if the option is in the money. Used in the functions aaQuanto_bin_cash() and aaQuanto_bin_asset().
option_type	The type of option: 1 = call, 2 = put.

Description of Outputs

Output Statistic	Description
fair value	The fair value of the option.
delta of underlying	The rate of change in the fair value of the quanto per one unit change in the current value of the underlying asset. This is the derivative of the quanto price with respect to the underlying current value.
delta of FX	Similar to delta of underlying but the derivative is with respect to the FX rate.
gamma of underlying	The rate of change in the value of delta of underlying per one unit change in the value of the underlying asset. This is the second derivative of the quanto price with respect to the underlying current value.
gamma of FX	Similar to gamma of underlying but the derivative is with respect to the FX rate.
theta	The rate of change in the fair value of the quanto per one day decrease of the option time. This is the negative of the derivative of the quanto price with respect to the option time (in years), divided by 365.
vega of underlying	The rate of change in the fair value of the quanto per 1% change in the volatility of the underlying (foreign) asset price. This is the derivative of the quanto price with respect to this volatility, divided by 100.
vega of FX	Similar to vega, but the derivative is with respect to the volatility of the FX rate.
rho of domestic	The rate of change in the fair value of the quanto per 1% change in the risk-free rate of the domestic currency, rate_dom. This is the derivative of the option price with respect to rate_dom, divided by 100.
rho of foreign	Similar to rho of domestic, but the derivative is with respect to the domestic risk free rate, rate_for. dividend yield, div_yield.
rho of dividend	Similar to rho of domestic, but the derivative is with respect to the dividend yield, div_yield.

For more information on inputs and outputs, please refer to the corresponding Function Reference documents accessible from the FINCAD XL main menu, Documents / Function References. For details about the calculation of Greeks, see the Greeks of Options on Non-Interest Rate Instruments FINCAD Math Reference document.

Examples

Context specific examples are presented for quanto forwards and options on indices and equities.

Example 1: Quanto forward on a stock index

Consider a forward contract on the stock index Nikkei 225 measured in US dollars ($) multiplied by 5. Suppose the index has a current value of ¥18700. Today is Aug. 1, 1997. The delivery date of the contract is Feb. 1, 1998. Suppose the dividend payout rate of the index is 1% (annually compounded, Actual/365 (fixed)) and the relevant risk-free interest rate in Japan is 2% (annually compounded, Actual/365 (fixed)). Suppose the annual volatility of the Nikkei index is 20% and that of the FX rate, dollar value per unit of yen ($/¥), is 0.10. Suppose further that the correlation between the return of the index and that of FX rate is 0.1. Use the function aaQuanto_fwd() to obtain the following results:

aaQuanto_fwd

Argument	Description	Example Data	Switch
price_ufor	underlying price (foreign)	18700
FX_fix	fixed FX rate, domestic currency per one unit of fixed foreign currency	5
d_exp	expiry date	1-Feb-1998
d_v	value date	1-Aug-1997
vlt_u	volatility of underlying	0.2
vlt_FX	volatility of foreign exchange rate	0.1
corr	correlation	0.1
rate_for	rate – foreign – annual Actual/365	0.02
cost_hldg	holding cost – annual – Actual/365	0.01
stat	stat list	1…8

Results

Statistics	Description	Value
1	fair value ($)	93870.85
2	delta	5.019831
3	gamma	0
4	theta	-2.01948
5	vega of underlying	-4.7321
6	vega of FX	-9.46419
7	rho of foreign rate	463.9107
8	rho of dividend	-468.492

Example 2: Quanto call option on a stock

Consider a call option on a British stock. The option has a payoff in US dollars with a fixed FX rate of 5 dollars per one pound. Suppose the stock has a spot price of 100 (£), the strike price is 90 (£). Today’s date is Aug. 1, 1997. The expiration date of the option is Feb. 1, 1998. Suppose the relevant sterling risk-free interest rate is 7% (annually compounded, Actual/365 (fixed)), that of the US dollars is 5% and the stock has a dividend payout rate of 3% (annually compounded, Actual/365 (fixed)). Suppose the annual volatility of the stock is 20% and that of the FX rate is 10%. Suppose the correlation between the return of the index and the return of the FX rate is 0.5. Use the function aaQuanto_opt() to obtain the following results:

aaQuanto_opt

Argument	Description	Example Data	Switch
price_ufor	underlying price (foreign)	100
ex_for	exercise price (foreign)	90
FX_fix	fixed FX rate, domestic currency per one unit of fixed foreign currency	5
d_exp	expiry date	1-Feb-1998
d_v	value date	1-Aug-1997
vlt_u	volatility of underlying	0.2
vlt_FX	volatility of foreign exchange rate	0.1
corr	correlation	0.5
rate_for	rate – foreign - annual – Actual/365	0.07
rate_dom	rate – domestic – annual – Actual/365	0.05
cost_hldg	holding cost – annual – Actual/365	0.03
option_type	option type	1	call
stat	stat list	1…9

Results

Statistics	Description	Value
1	fair value ($)	63.12154
2	delta of underlying	4.098718
3	gamma of underlying	0.091669
4	theta per day	-0.07295
5	vega of underlying	0.825397
6	vega of FX	-0.20435
7	rho of domestic rate	-0.3009
8	rho of foreign rate	1.910373
9	rho of dividend	-1.95882

Example 3: Quanto binary option on an equity

Suppose in example 2 the payoff of the option is cash or nothing: if the option at the expiration date is in the money, then the holder of the option gets a fixed amount of cash; if the stock value is out of the money, then the holder gets nothing. Suppose the cash amount is $20. Use the function aaQuanto_bin_cash to obtain the following results:

aaQuanto_bin_cash

Argument	Description	Example Data	Switch
price_ufor	underlying price (foreign)	100
ex_for	exercise price (foreign)	90
d_exp	expiry date	1-Feb-1998
d_v	value date	1-Aug-1997
vlt_u	volatility of underlying	0.2
vlt_FX	volatility of foreign exchange rate	0.1
corr	correlation	0.5
rate_for_ann	rate – foreign - annual – Actual/365	0.07
rate_dom_ann	rate – domestic – annual – Actual/365	0.05
div_yield	dividend yield	0.03
cash	cash payment	20
option_type	option type	1	call
stat	stat list	1…9

Results

Statistics	Description	Value
1	fair value ($)	15.21249
2	delta of underlying	0.407359
3	gamma of underlying	-0.02618
4	theta per day	0.013204
5	vega of underlying	-0.26671
6	vega of FX	-0.02056
7	rho of domestic rate	-0.07252
8	rho of foreign rate	0.188583
9	rho of dividend	-0.20102

References

[1] Baxter, M. and Rennie, A. (1996), Financial Calculus, Cambridge, Cambridge University Press.

[2] Hull, John, (1997), Options, Futures, and Other Derivatives, 3rd ed., Upper Saddle River, Prentice Hall.

Disclaimer

With respect to this document, FinancialCAD Corporation (“FINCAD”) makes no warranty either express or implied, including, but not limited to, any implied warranty of merchantability or fitness for a particular purpose. In no event shall FINCAD be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of the use of this document or the information contained in it. This document should not be relied on as a substitute for your own independent research or the advice of your professional financial, accounting or other advisors.

This information is subject to change without notice. FINCAD assumes no responsibility for any errors in this document or their consequences and reserves the right to make changes to this document without notice.