Swaps

Introduction

An interest rate swap is a contractual agreement between two counterparties to exchange cash flows on particular dates in the future. There are two types of legs (or series of cash flows). A fixed rate payer makes a series of fixed payments and at the outset of the swap, these cash flows are known. A floating rate payer makes a series of payments that depend on the future level of interest rates (a quoted index like LIBOR for example) and at the outset of the swap, most or all of these cash flows are not known. In general, a swap agreement stipulates all of the conditions and definitions required to administer the swap including the notional principal amount, fixed coupon, accrual methods, day count methods, effective date, terminating date, cash flow frequency, compounding frequency, and basis for the floating index. More information and other references can be found in [2] and [3].

Interest Rate Swaps

An interest rate swap can either be fixed for floating (the most common), or floating for floating (often referred to as a basis swap). In brief, an interest rate swap is priced by first present valuing each leg of the swap (using the appropriate interest rate curve) and then aggregating the two results.

Foreign-Exchange (FX) Swaps

An FX swap is where one leg’s cash flows are paid in one currency () while the other leg’s cash flows are paid in another currency (). An FX swap can be either fixed for floating, floating for floating, or fixed for fixed. In order to price an FX swap, first each leg is present valued in its currency (using the appropriate curve for the currency). Let these values be and , respectively. Then, given the FX spot rate (in units of per ), the fair value of the swap is given by:

, or

Analysis Supported

FINCAD functions can be used for the following:

· Generic interest rate swaps, allows custom structure (variable notional, variable fixed leg coupon)

· Cross-currency and basis swaps

· % Libor swaps

· Non-generic interest rate swaps

· Fixed legs

· Floating Rate Notes

Technical Details

To value a swap we need to determine the fair value of each leg of the transaction. In an interest rate swap, the fixed leg is fairly straightforward since the cash flows are specified by the coupon rate set at the time of the agreement. Valuing the floating leg is a little more complex since, by definition, the cash flows change with future changes in the interest rates. The valuation of both legs of the swap is examined in detail below.

Fixed Leg of a swap

Equation 1

where

= present value of cash flows for the fixed leg

= notional principal amount

= fixed coupon rate

= summation counter

= number of coupons payable between value date and maturity date

= accrual factor between dates and based on specified accrual method

= zero coupon discount factor at date

Floating Leg of a swap

Equation 2

where:

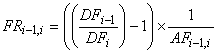
Equation 3

and

= present values of cash flows for floating leg

= notional principal amount

= implied forward rate from date to date

= accrual factor from date to date i based on specified accrual method

= number of cash flows from settlement date to the maturity date

= zero coupon discount factor at date

= summation counter

Interest Rate Swap

As previously defined, a swap is a contractual agreement to exchange net cash flows for a specified pay leg and receive leg, each of which may be either fixed or floating. The fair value of the swap is the difference between the values of the two streams of cash flows. Since we already know how to value each of the components, it is easy to value the swap. For example, if one counterparty was paying fixed and receiving floating the swap value = - fair value of the fixed leg + fair value of the floating leg. The other counterparty to the swap simply reverses the signs on the two legs to obtain fair value.

floating vs. fixed

fair value = fair value of fixed leg - fair value of floating leg

fixed vs. floating

fair value = fair value of floating leg - fair value of fixed leg

Swap Risk Statistics

Several risk statistics are calculated for interest rate swaps including modified duration, convexity, and basis point value. These risk statistics are based on the risk statistics for the individual legs of the swap, as described below.

For the individual fixed and floating legs of the swap, the modified duration, convexity and basis point value are calculated numerically by bumping the accruing and discounting curves. The rates in the accruing and discounting curves are bumped up by a small amount , and down by . These bumped curves are then used to obtain the bumped up and bumped down fair value (FV) of the fixed leg and the floating leg. The risk statistics for the individual legs are then calculated as follows:

It should be noted that when calculating the above risk statistics for the individual legs of the swap, it is assumed that there is payment of principal at maturity regardless of the settings used for the swap.

The above risk statistics from the individual legs of the swap are then used to calculate the risk statistics for the swap as follows:

Functions

Instrument type	Valuation functions	Cash flow functions	Utility functions
Fixed legs	aaFixlg_p aaFixlg2_p aaFixlg_fs_p	aaFixlg_cfs aaFixlg2_cfs aaFixlg_cfx aaFixlg2_cfx aaFixlg_fs_cfx aaFixlg_fs_cfs	aaFixlg_accrued aaFixlg2_accrued
Fixed legs (custom coupon tables)	aaFixlg_dgen_p aaFixlg2_dgen_p	aaFixlg_dgen_cfs aaFixlg2_dgen_cfs aaFixlg_dgen_cfx aaFixlg2_dgen_cfx	aaFixlg_dgen_accrued aaFixlg2_dgen_accrued
Floating legs (compounding resets)	aaFRN aaFRN2 aaFRN3 aaFRN_fs aaFRN2_fs aaFloatlg_p aaFloatlg2_p aaFloatlg3_p	aaFRN_cf aaFRN2_cf aaFRN3_cf aaFRN_fs_cf aaFRN2_fs_cf aaFloatlg_cf aaFloatlg2_cf aaFloatlg3_cf	aaFRN_Tables aaFRN_tables2
Floating legs (constant maturity)		aaFRN_CM_cf
Floating legs (averaging resets)	aaFRNavg aaFRNavg_fs	aaFRNavg_cf aaFRNavg_fs_cf	aaFRNavg_Tables aaFRNavg_Tables_fs
Plain Vanilla Swaps (both legs)	aaSwap_p aaSwap2_p aaSwap3_p aaSwap4_p	aaSwap_cf aaSwap2_cf aaSwap3_cf aaSwap4_cf

Naming Conventions

Function Suffix	Description
cf	a general cash flow table
cfs	a simple cash flow table with no inputs for a discount factor curve
cfx	an extended cash flow table, typically includes a discount factor curve to calculate present values
p	output prices and risk statistics
accrued	output accrual information including some statistics
Tables	ability to input a table of rates
fs	used for non-generic swaps; ability to input specific coupon payments and fixed payments in separate periods
dgen	used for custom structured swap; ability to input variable notional and variable fixed leg coupon rate

Market Data Requirements

The market data that is needed are generally the discount factor curves for accruing and discounting cash flows for the floating leg, and the discount factor curve for discounting the fixed leg. These discount factor curves are swap curves that are built using the FINCAD function aaSwap_crv3. In order to construct the swap curve, the function uses cash rates, future or FRA rates, and par swap rates. When valuing a cross-currency swap, the spot exchange rate between the two currencies is needed, as are the basis spreads. These basis spreads are basically a market quote of a premium of one currency over the other. To properly value a cross-currency swap, these spreads need to be included in the valuation. These spreads can be included in the FINCAD valuation by using the function aaDFCurve_AddXCBasisSpreads_dgen.

Further details on these functions are provided in the following FINCAD Math Reference documents:

· Interest Rate Curve Generation

· Interest Rate Curve Utilities

Examples

Example 1: Vanilla Fixed for Floating Interest Rate Swap

From a counterparty’s perspective, a swap can be viewed as two series of cash flows; outflows are known as the “pay leg” and inflows are known as the “receive leg”. Suppose the following situation exists:

Company A	Company B
‘AA’ credit rating	‘A’ credit rating
can issue fixed debt at 7%	can issue fixed debt at 7.65%
can borrow floating at LIBOR + 10 bps	can borrow floating at LIBOR + 30 bps
believes rates will be stable or falling, wants floating rate debt	wants secure funding - fixed debt

The current swap rate is 7.2% vs. LIBOR flat. Both companies will find it advantageous to enter into the following swap:

The net funding cost for each company can be represented as follows:

Company A		Company B
Pay:	7% fixed	Pay:	LIBOR + 30bps
Receive:	7.2% fixed	Receive:	LIBOR floating
Pay:	LIBOR floating	Pay:	7.2% fixed
Net:	LIBOR - 20bps	Net:	7.5% fixed

Company A effectively borrows floating at LIBOR - 20bps for a net savings of 30bps compared to funding by way of LIBOR directly.

Company B effectively borrows fixed at 7.5%, a 15bps discount compared to issuing fixed debt at 7.65%.

Example 2: Calculating the Fair Value for the Fixed Leg of a Swap

For the fixed leg of the swap, in this example, we use aaFixlg2_p and aaFixlg2_cfx. The detailed usage of the fixed leg functions are shown in the following sample workbook:

Fair Value for the Fixed Leg

Example 3: Calculating Fair Value for the Floating Leg of a Swap

To value the floating leg of the swap we use aaFRN3_cf and aaFRN3. The detailed usage of the floating leg functions are shown in the following workbook:

Fair Value for the Floating Leg

Example 4: Calculating Fair Value for a Fixed vs. Floating Interest Rate Swap

Using the data from the above fixed leg and floating leg examples, we can determine the fair value for a fixed vs. floating swap (i.e. pay fixed and receive floating). The detailed valuation and comparison between the fixed and floating leg are shown in the following workbook:

Fair Value for a Fixed vs. Floating IR Swap

Example 5: Calculating Fair Value for a Cross-Currency Swap

Cross-currency swaps (also known as foreign-exchange or FX swaps) differ from single currency swaps in that each leg of the swap is denominated in a separate currency. Like single currency swaps, cross-currency swaps can come in any one of three types: fixed vs. fixed, fixed vs. floating, or floating vs. floating. Of these three types, floating vs. floating is the most fundamental since it can be combined with single currency swaps to synthetically create any of the other types. This floating vs. floating cross-currency swap is also known as a basis swap, and is the main type for which market quotes are available. The detailed worksheet depicting this example can be found at:

Fair Value for a Cross Currency Swap

Related Functions

Similar Instruments

Topic	Functions
Par swap rates	aaParSwap aaParSwap_fs

Utility and Support Functions

Topic	Functions
Interest rate curve generation	aaSwap_crv aaSwap_crv2 aaSwap_crv3 aaSwap_crv_avg aaSimpleSwapCrv aaEDFut_CnvxAdj_HW

References

[1] Boenkost, Wolfram, and Schmidt, Wolfgang M., (2005), ‘Cross Currency Swap Valuation’, Section 2.1.

[2] Flavell, Richard, (2002), Swaps and Other Derivatives, Wiley Finance

[3] Miron, Paul, Swannell, Philip, (1991), Pricing and Hedging Swaps, EuroMoney Books.

Disclaimer

With respect to this document, FinancialCAD Corporation (“FINCAD”) makes no warranty either express or implied, including, but not limited to, any implied warranty of merchantability or fitness for a particular purpose. In no event shall FINCAD be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of the use of this document or the information contained in it. This document should not be relied on as a substitute for your own independent research or the advice of your professional financial, accounting or other advisors.

This information is subject to change without notice. FINCAD assumes no responsibility for any errors in this document or their consequences and reserves the right to make changes to this document without notice.

Copyright

Copyright © FinancialCAD Corporation 2008. All rights reserved.