Standard American Style Options (Cox-Rubinstein Binomial)
Overview
Standard American style options are call and put options
which can be exercised at any time during the life of the option. An American style option is always at least as
valuable as its counterpart, the European style option, which can be exercised
only on the expiration date. Valuation
of American style options is generally more difficult than the valuation of
European style options. In fact, for
standard European options a closed form solution for their pricing, the
Black-Scholes solution, exists. On the
other hand, for American style options no (simple) closed form solution is
available. Several numerical methods
have been proposed and used. Examples
include finite difference and finite element methods. However, the most popular method is the
Cox-Rubinstein binomial model.
The Cox-Rubinstein Binomial Model
In 1979 Cox, Ross and Rubinstein proposed a numerical
method for pricing American style options using a binomial tree. This is a tree that represents possible paths
that might be followed by the underlying asset's price over the life of the
derivative. The model works by dividing
the time to expiration into a number of time intervals and over each time
interval, the model assumes that the price of the underlying moves up or down
to certain values. The magnitude of
these moves is determined by the volatility of the underlying and the length of
the time interval. The time slices and
the assumed prices of the underlying asset at these times form the nodes of a
binomial tree. The method for valuing
American style options generalizes that for valuing European style options. Briefly, here are the main steps involved in
valuing a European style option using a binomial tree.
1.
Calculate the option value at each of the end
nodes (leaves) of the tree.
2. Move
on to the previous time step and calculate the option value at each node on
this time slice from the option values at its descendent nodes.
3. Continue
in this manner until the option at all of the nodes of the tree is valued.
The option value at the root of the tree is then the
price of the option. It can be shown
that as the steps of the tree increases, this option value converges to that of
the Black-Scholes model.
To value an American option, one more step is
added at each node (except for the end nodes):
4. Check
if early exercise is optimal after an option value is calculated at the node. The option price at this node is then the
greater of this value and the payoff of early exercise. See the
details below.
The following are basic assumptions for option
pricing models. The binomial model is
also based on these assumptions:
·
Interest rates are constant over the life of an
option.
·
The price of an underlying is lognormally
distributed.
·
The volatility of the price of an underlying is
constant over the life of the option.
Formulas & Technical Details
The binomial model
Binomial modeling of option prices approximates the true
option price by discretizing both the stock price and time. This method is intuitive and not too
mathematically complicated. The
following is a sketch of the binomial model for pricing options on stocks
paying no dividends.
1.
One step binomial models
The simplest way
to understand binomial trees is to first look at a one step tree. Let 
be the time to
expiration of a call option on a stock paying no dividends. Let 
be the current price
of the stock and 
the strike price of
the option. Let 
denote the value of
the option. Suppose 
is the relevant
risk-free interest rate which is assumed to be constant during the life of the
option.
Suppose at time the stock can take
only two values. It either goes up to 
or goes down to 
, where 
and 
. For this case the
pricing of the option is simple. If the
value is , the option price 
at is:
Similarly, if the value of the stock at time is 
, then the option price at is:
To study the price of the option, consider the
following riskless portfolio: a long
position in Δ shares of
the stocks and a short position in one such option. Then the value of the portfolio will be 
if the stock price
goes up, or 
if the stock price
goes down. Since the portfolio is
riskless it follows that:
and therefore
Equation 1
Since the cost of setting up the portfolio is 
,
.
Substituting from Equation 1
the current price of the option is
.
where
For the one step model the American style option
and the European style option is the same.
2. Two
step binomial models
Divide the time interval 
into two intervals of
equal length. Let 
be the volatility of
the stock, 
and 
. Then at time 
the stock has two
possible values 
and , and at time it has three possible
values: 
, 
, and 
(note that 
). See the following
graph.
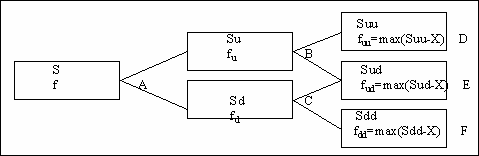
Figure 1
The option values at the end nodes (leaves) 
, 
and 
are simply the
intrinsic values of the option. If the option is European, then the option
value 
at node 
is:
where
If the option is American, then the option value
at this node is the greater of this value and the intrinsic value of the
option, that is
.
The option value at 
can be determined analogously.
Finally, the option value at node 
can be determined from
and 
in a similar way. This value is the value of the option.
The idea for valuing options using a general 
step tree is the same
as that for a two step tree.
3. Dividends
With a minor modification, the above binomial
model can be used to model options on underlyings which pay dividends. Note
that the volatility in this case is the volatility of the spot price minus the
dividends. See the books of
4. Futures
The valuation of options on futures is a little
different from the valuation of options on stocks and other underlying assets. However, one can modify the binomial model
(mathematically, letting r=0 in the expression of p) to value options on
futures. See the details in the book of
Cox and Rubinstein [2]
(P. 418).
5. Repo
Spread and Continuous Dividend Yield
The repo agreement is a contract whereupon two
parties exchange collateral (in this case the underlying asset) for cash, with
an agreement to perform the reverse exchange at a predetermined time in the
future when the cash has accumulated interest at a predetermined rate: the
“repo rate” [1]. The repo rate represents the rate of a
“repurchase agreement” that is usually necessary when short selling the
underlying asset. Therefore, the repo
spread input need only be used when hedging the option requires a short
position in the underlying (that is for long calls or short puts); otherwise,
enter a zero repo spread. The repo
spread is analogous to a continuous dividend yield, in that in the risk-neutral
measure the underlying grows at the risk-free rate minus the repo spread (or
continuous dividend yield).
The repo spread input to the function aaBIN2dcf()
can be entered as a single spread or a discount factor curve. If entering a single spread, this spread
equals the risk-free rate of interest minus the repo rate quoted in the market
when both rates are quoted as annual, act365(fixed) (conversion to this rate basis
and accrual factor can be done with the FINCAD function aaConvert_cmpd2()). A positive repo spread describes the case
where the repo rate is greater than the risk-free rate. If you wish to enter the repo spread as a
“discount factor” curve, create this curve by the following procedure: First construct the risk-free discount factor
curve from money market rates (using, for example, one of FINCAD’s curve
bootstrapping functions such as aaSwapCrv())
and the repo rate “discount factor” curve in a similar way from quoted repo
rates of different tenors. If the dates
in these two discount factor curves do not match, find the missing discount
factors by interpolation, using aaInterp(). The repo spread “discount factor” curve can
then be created by taking the ratio of the risk-free to the repo rate discount
factors on each date (more explicitly
the risk-free discount factor divided by the repo rate discount factor, this
ratio will be greater than one if the repo rate is greater than the risk-free
rate).
This input also provides the ability to enter a term
structure of dividend yields. For
example, the case where discrete dividends are known up to a particular date
and assumed continuous after this date, can be handled by using a combination
of discrete dividends and the discount factor input. Simply set the continuous dividend yield
discount factor equal to one on all dates prior to the last known dividend date
to achieve the desired result.
Calculate Risk Statistics from a binomial tree.
The option risk statistics delta, gamma and theta may be
calculated from the binomial tree.
Delta
The delta is given as in Equation 1,
where
and
with the number of steps of
the tree.
Gamma
Theta
Generally, the other statistics may be
approximated by considering the differences in the option price when the
relevant parameters change. For more
details about the calculation of Greeks, see the Greeks of Options on non-Interest Rate
Instruments FINCAD Math Reference document.
FINCAD Functions
The following functions calculate fair values, risk
statistics and implied volatilities (given option price) for American style
call and put options on spot stocks, stock indices, commodities and FX rates.
aaBIN2(price_u,
ex, d_exp, d_v, vlt, rate_ann, acc_rate, cost_hldg, acc_cost_hldg, option_type,
iter, stat)
aaBIN2dcf(price_u,
ex, d_exp, d_v, vlt, risk_free_rate,
repo_spread, interp, div_obj,
option_type, iter, stat)
aaBIN2_iv(price_u,
ex, d_exp, d_v, price, rate_ann, acc_rate, cost_hldg, acc_cost_hldg,
option_type, iter)
aaBIN2_ik(price_u,
d_exp, d_v, vlt, price, rate_ann, acc_rate, cost_hldg, acc_cost_hldg, option_type,
iter, stat)
aaBIN2_iu(ex,
d_exp, d_v, vlt, price, rate_ann, acc_rate, cost_hldg, acc_cost_hldg,
option_type, iter, stat)
aaBINdcf(price_u,
ex, d_exp, d_v, vlt, rate_ann, acc_rate, div_obj, option_type, iter, stat)
aaBINdcf_iv(price_u,
ex, d_exp, d_v, vlt, rate_ann, acc_rate, div_obj, option_type, iter, stat)
aaBINdcf_ik(price_u,
d_exp, d_v, vlt, rate_ann, acc_rate, div_obj, option_type, iter, stat)
aaBINdcf_iu(ex,
d_exp, d_v, vlt, price, rate_ann, acc_rate, div_obj, option_type, iter, stat)
The following functions deal with valuation of
options on futures (e.g., commodity futures and FX forwards) and on Eurodollar
futures.
aaBIN(price_u,
ex, d_exp, d_v, vlt, rate_ann, option_type, stat, option_on, iter, acc)
aaBIN_iv(price_u,
ex, d_exp, d_v, price, rate_ann, option_type, stat, option_on, iter, acc)
aaBIN_ED_fut(bpv,
price_u, ex, d_exp, d_s, vlt, rate_ann, option_type, stat, iter, acc)
aaBIN_ED_fut_iv(bpv,
price_u, ex, d_exp, d_s, price, rate_ann, option_type, iter, acc)
There
are several other types of American style call / put option functions
available:
·
Quanto Options: aaQuanto_Bin2()
·
Options
with Varying Strikes and Variable Rates: there are several functions available that
allow variable strike prices, variable rates, lockout periods, etc.
·
FX Specific Options:
aaFX_BIN()
Description of Inputs
|
Input Argument |
Description |
|
price_u |
Current value of the underlying asset |
|
ex |
Strike price |
|
d_exp |
Expiry date of the option |
|
d_v |
Value date |
|
vlt |
The annualized volatility of the underlying asset (not an
input in the implied volatility
functions). |
|
rate_ann, cost_hldg, |
Also denoted rate1 and rate2, respectively. These rates are quoted on an annually compounded, Act / 365 (fixed) basis. If the underlying is an equity, rate1 is the relevant
risk-free rate. Rate2 is the
annualized dividend yield. If the underlying is a forward or futures price, rate2
should be set equal to the risk-free rate1. If the underlying is an FX (foreign exchange) rate, and
quoted on a domestic per foreign basis, rate1 should be the risk-free
domestic rate and rate2 the risk-free foreign rate. If the underlying is an FX rate, and quoted on a foreign
per domestic basis, rate1 should be the risk-free foreign rate and rate2 the
risk-free domestic rate. If the underlying is a commodity, then rate2 should be set
to the annualized holding cost of the commodity, including storage and
insurance costs as well as marginal convenience value. |
|
risk_free_rate |
Risk free rate of
interest for aaBIN2dcf(). This
can be entered as a single rate, assumed to be annual compounding with
accrual method Act365(fixed), a single rate and a compounding frequency
(switch 43), a single rate, a compounding frequency and an accrual method
(switch 331), or as a discount factor curve. |
|
repo_spread |
This rate represents
the difference between the risk-free interest rate and the repo rate. In the presence of a repo spread, the
underlying asset grows at the risk-free rate minus the repo spread. aaBIN2dcf() only. |
|
interp |
Interpolation technique for the discount factor
curves. aaBIN2dcf()
only. |
|
acc, acc_rate, acc_cost_hldg |
Accrual method. It
can be one of the five choices: Actual/365 (fixed), Actual/360, Actual/365
(actual), 30/360 and Euro 30E/360.
(For aaBIN2dcf()
acc_rate can take on any value in FCSW331). |
|
iter |
The number of steps of the binomial tree. |
|
option_type |
The type of option: 1 = call, 2 = put. |
|
stat |
See the description of the outputs. |
|
div_obj |
Dividend payment table. The table has two columns, the dividend
payment dates (left column) and the corresponding dividend payment amounts
(right column). Only used in aaBINdcf(),
aaBINdcf_iv()
and aaBIN2dcf(). |
|
option_on |
A switch, which is set to 1 for options on futures; 2 for
options on stock or securities paying no dividends. Only used in the functions aaBIN()
and aaBIN_iv().
|
|
price |
The given option price. Only used in the implied volatility
functions. |
Description of Outputs
|
Output Statistic |
Description |
|
fair value |
The fair value of the
option. |
|
delta |
The rate of change in
the fair value of the option per change in the current value of the
underlying asset. This is the
derivative of the option price with respect to the current value of the
underlying. |
|
gamma |
The rate of change in
the value of delta per change in the current value of the underlying asset. This is the second derivative of the option
price with respect to the current value of the underlying. |
|
theta |
The rate of change in
the fair value of the option per one day decrease in the option time. This is the negative of the derivative of
the option price with respect to the option time (in years), divided by 365. |
|
vega |
The rate of change in
the fair value of the option per 1% change in volatility. This is the derivative of the option price
with respect to the volatility, divided by 100. |
|
rho of rate |
The rate of change in
the fair value of the option per 1% change in the risk-free rate, rate_ann. This is the derivative of the option price
with respect to the risk-free rate, divided by 100. |
|
rho of holding cost,
rho of repo spread |
The rate of change in
the fair value of the option per 1% change in the holding cost, cost_hldg (or
a 1% change in the repo spread for aaBIN2dcf().) This
is the derivative of the option price with respect to cost_hldg, divided by
100. If the underlying is futures, this statistic is not available. |
Examples
Context specific examples are presented for American-style
options on stocks, commodity futures and foreign exchange rates. For options involving different underlyings,
see the remarks following these examples.
Example 1: Indices
Consider an American style call option on an index which
has a current value of 910. Suppose the
strike price is 920. Today is Aug. 1,
1997. The expiration date of the option
is Feb. 1, 1998. Suppose the relevant
risk-free interest rate (annually compounded, Actual/365 (fixed)) is 7% and the
dividend payout rate over the life of the option (annually compounded,
Actual/365 (fixed)) is 5%. Suppose the
annual volatility of the stock is 12%. Using
a 200 step binomial model and the function aaBIN2() we obtain
the following results:
aaBIN2
|
Argument |
Description |
Example Data |
Switch |
|
price_u |
underlying price |
910 |
|
|
ex |
exercise price |
920 |
|
|
d_exp |
expiry date |
1-Feb-1998 |
|
|
d_v |
value (settlement) date |
1-Aug-1997 |
|
|
vlt |
volatility |
0.12 |
|
|
rate_ann |
rate – annual compounding |
0.07 |
|
|
acc_rate |
accrual method – risk free rate |
1 |
actual/365 (fixed) |
|
cost_hldg |
holding cost |
0.05 |
|
|
acc_cost_hldg |
accrual method – holding cost |
1 |
actual/365 (fixed) |
|
option_type |
option type |
1 |
call |
|
iter |
number of time steps |
200 |
|
|
stat |
stat list |
1…7 |
|
Results
|
Statistics |
Description |
Value |
|
1 |
fair value |
29.55308 |
|
2 |
delta |
0.497785 |
|
3 |
gamma |
0.005034 |
|
4 |
theta |
-0.10019 |
|
5 |
vega |
252.9984 |
|
6 |
rho of rate |
202.6499 |
|
7 |
rho of cost of holding |
-210.644 |
Suppose in the above example the volatility of
the index is not known but the quoted price of the option is 29.55308 (the
option value obtained above). Calling aaBIN_iv(),
using the parameters above and the quoted price, we obtain an implied
volatility of 12%, as expected.
Example 2: Stocks paying discrete dividends
Consider an American call option on a stock which has a
spot price of 100. Suppose the strike
price is 105. Today is Aug. 1, 1997. The expiration date of the option is Feb. 1,
1998. Suppose the relevant risk-free
interest rate is 7% (annually compounded, Actual/365 (fixed)) and the stock
pays dividends of 0.5 dollars on the 20th of September, December, March and
June during the life of the option. Suppose
the annual volatility of the stock is 12%. Using a 200 step binomial model and the
function aaBINdcf()
we obtain the following results:
aaBINdcf
|
Argument |
Description |
Example Data |
Switch |
|
price_u |
underlying price |
100 |
|
|
ex |
exercise price |
105 |
|
|
d_exp |
expiry date |
1-Feb-1998 |
|
|
d_v |
value (settlement) date |
1-Aug-1997 |
|
|
vlt |
volatility |
0.12 |
|
|
rate_ann |
rate – annual compounding |
0.07 |
|
|
acc_rate |
accrual method – risk free rate |
1 |
actual/365 (fixed) |
|
div_obj |
dividend table |
see below |
|
|
option_type |
option type |
1 |
call |
|
iter |
number of time steps |
200 |
|
|
stat |
stat list |
1…7 |
|
Dividend table t_14
|
dividend date |
dividend payment |
|
20-Sep-1997 |
0.5 |
|
20-Dec-1997 |
0.5 |
|
20-Mar-1998 |
0.5 |
|
20-Jun-1998 |
0.5 |
Results
|
Statistics |
Description |
Value |
|
1 |
fair value |
2.313675 |
|
2 |
delta |
0.402271 |
|
3 |
gamma |
0.045994 |
|
4 |
theta |
-0.01584 |
|
5 |
vega |
27.79036 |
|
6 |
rho of rate |
18.1532 |
Note: The
function aaBINdcf()
ignores the dividends which are beyond the life time of the option.
Example 3: Commodity Futures
Consider an American-style call option on 1000 barrels of
6 month's crude oil futures with a strike price of $25 per barrel. The current price of 6 month's crude oil
futures is $24 per barrel. Today's date
is April 1, 1997. The expiration date of
the option is Sept. 28, 1997. Suppose
the relevant risk-free interest rate over the life of the option is 3%,
(annually compounded, Actual/365), and the annual volatility of the futures
price is 20%. Using the function aaBIN()
we obtain the following results:
aaBIN
|
Argument |
Description |
Example Data |
Switch |
|
price_u |
underlying price |
24 |
|
|
ex |
exercise price |
25 |
|
|
d_exp |
expiry date |
28-Sep-1997 |
|
|
d_v |
value (settlement) date |
1-Apr-1997 |
|
|
vlt |
volatility |
0.20 |
|
|
rate_ann |
rate – annual compounding |
0.03 |
|
|
option_type |
option type |
1 |
call |
|
stat |
stat list |
1…6 |
|
|
option_on |
underlying interest |
1 |
option on a futures contract |
|
iter |
number of time steps |
200 |
|
|
acc |
accrual method |
1 |
actual/365 (fixed) |
Results
|
Statistics |
Description |
Value |
|
1 |
fair value per barrel |
0.916605 |
|
2 |
delta |
0.407878 |
|
3 |
gamma |
0.114867 |
|
4 |
theta |
-0.00355 |
|
5 |
vega |
6.479199 |
|
6 |
rho of rate |
4.083225 |
Fair
value of the option = 1000 * fair value per barrel =
916.6($)
Example 4: Foreign Exchange Rates
Consider an American style put option on the exchange rate
of £/$, sterling pounds per one unit of US dollar. The current exchange rate is 0.61 and the
strike price is 0.62. Suppose the
current risk-free interest rate of sterling is 7% (annually compounded,
Actual/365 (fixed)) and that of the U.S. dollar is 5%. Today’s date is Aug. 1, 1997. The expiration date of the option is Aug. 1,
1998. Suppose the annual volatility of
the exchange rate is 12%. Using a 200
step binomial tree and the function aaBIN2() we obtain
the following results:
aaBIN2
|
Argument |
Description |
Example Data |
Switch |
|
price_u |
underlying price |
0.61 |
|
|
ex |
exercise price |
0.62 |
|
|
d_exp |
expiry date |
1-Aug-98 |
|
|
d_v |
value (settlement) date |
1-Aug-97 |
|
|
vlt |
volatility |
0.12 |
|
|
rate_ann |
rate – annual compounding |
0.07 |
|
|
acc_rate |
accrual method – risk free rate |
1 |
actual/365 (fixed) |
|
cost_hldg |
holding cost |
0.05 |
|
|
acc_cost_hldg |
accrual method – holding cost |
1 |
actual/365 (fixed) |
|
option_type |
option type |
2 |
put |
|
iter |
number of time steps |
200 |
|
|
stat |
stat list |
1…7 |
|
Results
|
Statistics |
Description |
Value |
|
1 |
fair value per dollar |
0.028892613 |
|
2 |
delta |
-0.49205498 |
|
3 |
gamma |
6.236142315 |
|
4 |
theta |
-2.4908E-05 |
|
5 |
vega |
0.231272097 |
|
6 |
rho of sterling rate |
-0.18510448 |
Suppose it is an option to sell $100,000. Then the fair value of the option is:
100000 * 0.028893
= 2889.26 (£)
Remark:
Equivalently, one can value the option with respect to the exchange rate
in $/£ by switching the values of rate_ann and cost_hldg
and change the option type from a put to a call. In more detail, the current price is 1.639344 ($/£). The strike price is 1.612903 ($/£), rate_ann = 0.05 and cost_hldg = 0.07. The function aaBIN2() gives the
fair value of the call option as 0.076395.
If the option is to sell $100,000 or
equivalently, to buy 100000 ´
0.62 £ (strike price), the cost is:
100000 * 0.62 * 0.076395 = 4660.099
($) = 2889.26 (£).
Tip: The
selection of the appropriate FX rate in valuing an option on FX rates can be
confusing. The following table lists all
of the different scenarios in the sterling/dollar FX market. One can simply follow this example in his/her
modeling.
|
buy/sell |
amount |
option type |
FX rate |
cost of option |
|
sell |
100 $ |
put |
£/$ |
100´option value (£) |
|
buy |
100 $ |
call |
£/$ |
100´option value (£) |
|
buy |
50 £ |
call |
$/£ |
50´option value ($) |
|
sell |
50 £ |
put |
$/£ |
50´option value ($) |
Remarks on Other Examples
Commodities
Most options on commodities are options on commodity
futures. However, one can also use aaBIN2()
to value options on commodity spot prices. To use this function one should identify first
the rates of storage cost, insurance cost and convenience yield of the underlying
commodity and then combine these rates to define the rate of the cost of
holding of the commodity. This value is
used as the value of the parameter cost_hldg.
Stocks modeled using continuous dividend payout rates
Valuation of options on stocks modeled using
continuous dividend payout rates is similar to the valuation of options on
indices.
References
[1]
Choudry, Moorad (2006), An Introduction to Repo Markets, 3rd ed.,
[3]
Disclaimer
With respect to this document,
FinancialCAD Corporation (“FINCAD”) makes no warranty either express or
implied, including, but not limited to, any implied warranty of merchantability
or fitness for a particular purpose. In no event shall FINCAD be liable to
anyone for special, collateral, incidental, or consequential damages in
connection with or arising out of the use of this document or the information
contained in it. This document should not be relied on as a substitute for your
own independent research or the advice of your professional financial,
accounting or other advisors.
This information is subject to
change without notice. FINCAD assumes no responsibility for any errors in this
document or their consequences and reserves the right to make changes to this
document without notice.
Copyright
Copyright © FinancialCAD Corporation
2008. All rights reserved.