Default Probability Curves and Default Correlations
Overview
In credit derivative valuation and credit risk management,
one of the fundamentally important issues is the estimation of default
probabilities and correlations. For
this, generally speaking, there are two ways: using historical default data or
using mathematical models. Historical
default data has played an important role in the estimation of default
probabilities. However, because default
events are rare, there is very limited default data available. Moreover, historical data reflects the historical
default pattern only and it may not be a proper indicator of the future. This makes the estimation of default
probabilities from historical data difficult and inexact. To use this same data to estimate default
correlations is even more difficult and more inexact. The market trend now is towards more and more
to the use of mathematical models that don’t rely on historical default data. Roughly speaking, there are two types of modeling
approaches for defaults, the structural approach and the reduced form approach.
The structural approach is based on a
firm’s asset and liability structure. The
reduced form approach is based on a firm’s debt trading data, such as bond
prices and, in particular, spreads of credit default swaps. Essentially the reduced form approach models
the market view of the strength of a firm while the structural approach tries
to predict a firm’s fundamentals. In
recent years, the reduced form approach has gained a lot of popularity due to
the rapid development of the credit default swap market.
The following four methods are the most popular estimation
methods of default probabilities:
1. Rating
transition matrix
There are dozens of rating agencies that provide yearly
rating migration and default data for corporations and governments. From this data a rating transition matrix can
be constructed. Such a matrix gives
transition probabilities for a corporation migrating, in one year, from one
rating level to another. Of particular
interest is the transition probability to default status.
2. Asset
price implied default probabilities (Merton’s structural model)
A firm’s value changes over time. When the value of a firm’s assets is higher
than its liabilities, it can always sell its assets to cover its liabilities. However, if a firm’s asset value drops to a
certain level, for example, to a level below the value of its liabilities, it
cannot generate enough cash to pay its liabilities. As a consequence, liabilities like the payment
of bond coupons, will default. Thus a
firm’s default probability can be forecast if one is able to model a firm’s
asset value. Merton introduced this idea
in his seminal work on corporate debt valuation. His model for a corporation’s total value is
the well-known Black-Scholes model, a geometric Brownian motion.
3. Bond
yield spreads implied default probabilities
Corporate bonds offer higher yields than benchmark bonds,
such as US treasury bonds. The higher
the default probabilities, the wider its bond yield spreads are, compared to
the benchmark. Hence, if a corporation
issues bonds, its bond yield spreads are a good data source for estimating
implied default probabilities of the firm. If a corporation does not issue bonds, one may
still be able to use bond data from another entity that has a similar risk
profile and a similar structure.
4. Credit
default swap spreads implied default probabilities
Given a default probability curve, a par default swap curve
can be calculated. Reversing this
process, one can construct a default probability curve from given par default
swap rates. Such a method is often
called bootstrapping.
The four methods have their advantages and
disadvantages. Using bond yield spread
to imply default probabilities is good in that it reflects a timely, market
view of a firm’s financial strength. It
is not so good because many firms do not issue bonds and many corporate bonds
are thinly traded and, therefore, not quoted on a timely basis. Ratings data is good because it is available
for a large number of firms and organizations.
However this data is historical and may lag present market conditions. Merton’s model is good because it attempts to
model the fundamentals of a company. It
can also give a timely estimation of a firm’s default scenario. The potential downside is that the model
requires several parameters and the key inputs of a firm’s asset value and
asset volatility are not easy to obtain. The bootstrap algorithm is good because par
default swap spreads reflect directly the market view on the default profile of
a bond issuer; it is not so good because par default spreads do not exist at
all for some bond issuers. Here one may
face the chicken and egg problem: in order to get par default spreads default
probabilities must be known, and vise versa in order to derive default
probabilities, par default swap spreads must be known. For the last few years the credit default swap
market has been developing rapidly, more and more credit default swap data
becomes available and the bootstrapping method is getting more and more
popular.
FINCAD provides
functions for forecasting default probabilities using any of the above four
methods and also provides functions for calculating first-to-default
probabilities, kth-to-default probabilities, all-to-default
probabilities, interpolating/extrapolating a default probability curve and for
calculating default correlations. For
the modeling of default correlations, see the section “Correlated defaults”.
In addition to
the above fundamental methods in building default probability curves, it is
also interesting and practically useful in establishing the relationship
between a default probability curves and a risky discount factor curve. FINCAD provides several functions handling
these relationships.
Formulas & Technical Details
Deriving default probabilities from bond yield spreads or bond prices
Suppose a company issued three bonds, bond 1, 2 and 3,
with maturities 
and principal of $1.
Suppose today’s quoted prices for the bonds are 
, and 
, respectively. Let 
be the risk
neutral probability of default of the company at time 
. Let 
, be the price of a risk-free bond with the same maturity and
coupon rate as those of bond 
. We assume that the bonds can only default at maturities . Let 
be the loss
of the 
bond at time 
Then:
where
is the forward price of bond j at time
is the discount
factor at time 
and
is the expected
recovery rate of bond 
.
Then, assuming that recovery rates and interest rates
are independent, we have:
Solve the above equation inductively to get:
.
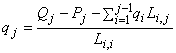The above can easily be extended to the case that
default can happen at any time. See
Deriving default probabilities from ratings transition matrix
Let 
be a one year rating
transition matrix with rating grades 
and default state 
, where 
is the
percentage that the firms of rating 
will
migrate to rating 
in one year. Note that 
for all 
and 
. Let 
. Then 
is the matrix of
transition probabilities and 
is the
frequency that a company with rating defaulted in one
year. It is easy to check that for any
integer the matrix 
, the product of the matrix 
multiplied by itself 
times, is also a
transition probability matrix. Suppose
that a firm’s rating follows a time homogeneous Markov process model with the
transition probability matrix. Then it
is easy to check that 
is the default
probability that a firm with rating will
migrate to rating in 
years. Given default probabilities in years 
one can approximate
default probabilities at any other time points.
Deriving default probabilities using Merton’s structural model
Suppose 
is the
asset value of a firm with the face value of liabilities 
. Under Merton’s model 
is a geometric
Brownian motion process and the firm defaults when the company’s asset value
goes below . We can call FINCAD functions aaDigital_AON and aaBarrier_eu
to calculate the risk neutral probabilities of default for checking default
only at a given time horizon or checking default for all times up to a given
time point.
Deriving default probabilities from par default swap spreads - bootstrapping
This is the inverse of calculating par default swap
spreads from a given default probability curve. Suppose par default swap spreads are given for
credit default swaps with maturities
. For the first period
, assuming the default probability curve has a constant
density 
in this period and
using the formula (see the Credit Default Swaps FINCAD Math Reference document) for
calculating the fair value of a credit default swap we can obtain. Thus the default
probability curve in the first time period is determined. Then assuming also the density of the
probability curve in the second period 
is also a constant 
, using the calculated density in the first period
and the formula for calculating the fair value of the second credit default
swap and the given par default swap rate of the second default swap we can
calculate . Thus the default
probability curve in the second period is determined. Iteratively, we can obtain the third and all
other periods.
Calculating first-to-default, nth-to-default and all-to-default
probabilities
If the default times of the names of a basket are independent,
first-to-default, nth-to-default, all-to-default probabilities can be
calculated through multiplication and integration of the default probability
curves of the basket. However, if the default times are not independent, no
simple formulas are available for these types of probabilities.
Case 1: Independent defaults
As an example, we consider the second–to-default probability
of a 4-name basket. Let:
be the default time of
name 
and 
its distribution, 
, where name 4 is the name of the counterparty. Then:
Prob(name 1 defaults second in the basket before time 
and before the
counterparty defaults)
= Prob(
+ Prob(
= 
The formula for 
-to-default probability before the counterparty defaults in a
general basket can be derived similarly. However, complexity increases as the number of
names increases.
The above method can also apply to derive the formula of
all-to-default probability before the counterparty defaults. This is clearly much simpler than the -to-default case.
Case 2: Correlated defaults
Model credit correlation using a normal credit index process
A credit index process is an unobservable (hidden)
random process that serves as a measure for the credit status of a credit
entity. The idea originates from
Merton’s seminal work on modeling corporate defaults. According to Merton the asset value of a
company drives the default event of the company. If the asset value goes below
a certain barrier, for example, the face value of the liabilities of the
company, the company will default. Here
the company’s asset value process serves the role of a credit index. From this model default probabilities can be
derived and the default correlation can also be implied from asset correlation.
One of the shortcomings of Merton’s model is that it
cannot make use of the default probabilities implied from market data, such as
bond prices. To overcome this problem
Theoretically given credit index correlations and
default barriers one can calculate default correlations as well as joint
default distributions. However, if
correlations cannot be ignored, there is no simple way to calculate
multidimensional joint default distributions and
With a credit index process we can determine the
default scenario by checking if this credit index falls below a certain level,
called a default barrier. Such a default barrier can be determined by any given
default probability. In more detail,
suppose 
is the standard
Brownian motion and the probability that a firm will default in years is 
. Then the default
barrier that the firm will default in years can be determined
by solving for x in the equation:
For a basket of reference entities if default barriers
and credit index correlations are known, Monte Carlo simulation can be used to
determine joint default probabilities of the entities. In more detail, one can first generate the
paths of the credit index process, i.e., paths of a correlated standard
multidimensional Brownian motion. By
checking, starting from smallest time point, the given time points one by one,
to see if the path of an entity is below the given default barriers, we can
determine if the firm will default and also find out the ordering of the
default times of the names in the basket.
Thus we can calculate the first-to-default, nth-to-default
before counterparty default and all-to-default before counterparty default
probability curves.
Credit index processes are intuitive and easy to
understand, but it suffers from low efficiency in terms of CPU time. Because default can happen at any time, one
would expect to check default at a sufficiently large number of time points for
the purpose of good accuracy. However,
the increasing of time points will rapidly increase the CPU time. When the basket is large, long CPU time may
become a serious issue.
Model credit correlation using a normal copula
Copulas are becoming more popular in credit
correlation modeling. The most commonly
used copula is the normal copula. A normal copula is simply a function of a
multi-dimensional normal distribution:
,
where
is an m-dimensional
copula,
is the distribution function of an k-dimensional normal
random vector with a mean vector of (0,…,0) and a standard deviation vector of
(1,…,1),
is the correlation
matrix, and
is the inverse of the
one-dimensional standard normal distribution.
Let 
and 
be the default time
and its distribution of name 
. To consider the default correlation of the basket (i.e.,
the correlations of the default times), we assume that the joint distribution
of the default times is:
,
where the correlation matrix of the m-dimensional
distribution underlying the normal copula is the asset (equity) correlation
matrix of the basket.
The right hand side of the above formula has a closed
form and looks quite appealing. Unfortunately, its calculation involves
integration over a multi-dimensional space. Numerical methods for the
calculation of such an integration are not sufficiently fast. Hence again
Here are the steps in using the copula method to
calculate the probability that name 
is the 
th-to-default before time and before the
counterparty defaults. Suppose the basket has names and name is the counterparty 
.
1. Generate an m-dimensional random vector 
from the distribution 
;
2. Calculate 
;
3. Sort 
in increasing order.
Denote the sorted vector as 
;
4. Check if 
and 
and 
.
5. Count the number of times that the above is
true and then calculate the probability required.
Calculating default correlation
Suppose that the joint default probability of company A
and B is 
and the default
probabilities of Company A and B are 
and 
, respectively. Then the default correlation of Company A and
B is defined as:
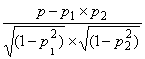
To calculate a default correlation the key is
then to calculate the joint default probability. For this one can use the asset correlation
and either a credit index process or a normal copula discussed above.
Hazard rate (default intensity ) curves
The hazard rate or failure rate is a term that is commonly
used in reliability theory, actuarial theory and statistics. Sometimes it is also called a failure rate. In
credit analysis it is often known as a default intensity. The hazard rate of a firm at a time point is defined as the
instantaneous probability of default given that the firm has not defaulted
prior to time . The relationship between a default probability and a hazard
rate can be derived easily. Following
the definition, for small time period 
:
where 
denotes the default time of the firm and
are the default probability and density at time 
respectively. It follows that:
Hence the relationship between a hazard rate curve
and a default probability curve is:
FINCAD Functions
aaCredit_DfltProb_bond2(d_v , bond_tbl, sprdorprice, df_crv_std,
intrp, hl, time_points, intrp_prob, calc_type):
Given a risk-free curve (or risk-free yields), and either
yield spreads or prices for a list of bonds issued by one company, forecasts
default probabilities at given time horizons.
Note that reasonable implied default
probabilities depend on reasonable bond yield spreads (or bond prices) and
reasonable recovery rates. Unreasonable
inputs can result in meaningless outputs, such as negative probability values. A rule of thumb is that higher default
probabilities are a result of higher expected loss. For example, if recovery rates are constant,
bond yield spreads must increase as time to maturity increases.
aaCredit_DfltProb_rating
(trans_matrix, time_points, intrp):
Given a one-year ratings transition matrix, forecasts
default probabilities at any given time horizons.
aaCredit_DfltProb_Merton(asset_val,
vlt, debt,cost_hldg, rate_ann, default_type, term):
Given the asset value and the asset volatility of a
company, forecasts default probabilities of the company at a given time
horizon.
aaCredit_DfltProb_DSSprd3(d_v,
cds_spread_tbl, acc, d_rul, adj_eff, adj_term, dGen_method, dfstd, intrp, time_points,
intrp_prob, hl, method_boot, calc_type, error_treat, output_type):
Bootstraps a default probability curve from a par credit
default spread curve. Various bootstrapping and date generation methods are
allowed. Upfront premium fees are also
incorporated.
Note that this function allows two
bootstrapping methods.
1.
assuming constant default density between two
consecutive CDS maturities of the given CDS spread curve;
2.
assuming constant hazard rate between two
consecutive CDS maturities.
It also allows three date generation methods:
backward, forward and IMM (for details on these methods, see the table Description of Input Parameters below). To bootstrap a default probability curve with
another less commonly used method, the method by interpolating the par CDS swap
curve, use the following function:
aaCredit_DfltProb_DSSprd2(d_v,
cds_sprd_tbl, acc, d_rul, df_crv_std, intrp, time_points, intrp_prob, hl, method_boot,
calc_type, error_treat, output_type).
However, this
function can only handle one date generation method: the backward method.
Moreover, it cannot handle upfront fees.
aaCredit_DfltProb_DSSprd_std(d_v,
cds_sprd_tbl, acc, d_rul, df_crv_std, intrp, time_points, intrp_prob, hl, method_boot,
mat_type, calc_type, error_treat, output_type):
Derives a default
probability curve from a par CDS spread curve using various bootstrapping
methods. Both standard and IMM
maturities are allowed. Upfront premium
fees are also incorporated.
This is a
simplified version of function aaCredit_DfltProb_DSSprd3.
aaCredit_ConvertDfltPtoDF(prob_crv,
rate_recover, acc_time, freq_prem, d_rul, df_crv_std, intrp, min_years, hl, calc_type):
Builds a risky discount factor curve from a default
probability curve and a risk-free discount factor curve.
aaCredit_ConvertDFtoDfltP(df_crv_risk,
rate_recover, acc_time, freq_prem, d_rul, df_crv_std, intrp, hl, time_points, intrp_prob,
calc_type):
Builds a default probability curve from a risky discount
factor curve and a risk-free discount factor curve.
Note : A risky discount factor curve derived
from a default probability curve is a simplified measure of the default profile
of a name. Hence results derived by the
use of such a risky discount factor curve can, theoretically, be less accurate
than that obtained through the direct use of the original default probability
curve.
aaCredit_DfltProbFirst_ind2(prob_bskt, intrp_prob, table_type):
Given default probability curves for a basket of names,
assuming independent defaults, derives first-to-default probability curves for
each name and for the basket.
aaCredit_DfltProb_first_MC2(prob_bskt, intrp_prob,
corr_mat_ent3, num_rnd, table_type):
Given default
probability curves for a basket of names and a credit index correlation matrix,
derives first-to-default probability curves for each name.
aaCredit_dfltProbRnk_ind(prob_bskt, intrp, rank, prob_type):
Given default probabilities of a basket of names and a
counterparty, assuming independent defaults, calculates
Kth-to-default-before-counterparty-default probabilities of each name and the
basket.
aaCredit_DfltProbRnk_MC(prob_bskt, intrp,
corr_mat_ent4, meth_corr, rank, mc_trial, prob_type):
Given default
probability curves for a basket of names and a credit index/asset correlation
matrix, derives first-to-default probability curves for each name and the
basket.
aaCredit_dfltProbAll_MC(prob_bskt, intrp_prob, corr_mat_ent4, meth_corr,
mc_trial, table_type):
Given default probabilities and credit index/asset
correlation of a basket of names and a counterparty, calculates
nth-to-default-before-counterparty-default probabilities of each name and the
basket
aaCredit_DfltBarrier_MC2(prob_crv, num_rnd, calc_prob):
Given a default probability curve, calculates default
barriers of a credit index process using Monte Carlo simulation or a
combination of a numerical method and
aaCredit_DfltCorr_MC(probordensity, prob_crv_ent2, corr,
num_rnd):
Given default probabilities and credit index correlation
of two credit names, calculates default correlation by
aaCredit_Interp_DfltProb(probordensity, prob_crv, time_points):
Interpolates and/or extrapolates a default
probability/density curve.
aaCredit_Interp_DfltProb2(prob_crv, time_points, intrp_prob, return_type):
Interpolates and/or extrapolates a basket default
probability curve.
aaCredit_convert_hazard(prob_crv_ent3, hazardorprob, intrp_prob, output_type):
Converts a hazard rate curve to a default probability
curve or vice versa.
Description of Inputs
|
Input Argument |
Description |
|
d_v |
Valuation date |
|
bond3_tbl |
A table of bonds with 15 columns: yield spread or price,
recovery rate, bond maturity date and other bond information (see aaBond3
for details.) |
|
sprdorprice |
A switch: 1 = yield spread, 2 = bond price. If it has the value of 1, the first column of the bond
table has the yield spreads of the bonds, otherwise, it has bond prices. |
|
yield_riskfree |
Risk free yield to maturity. |
|
hl |
|
|
df_crv_std, dfstd |
Risk-free discounting factor curve |
|
intrp |
Interpolation method |
|
trans_matrix |
A rating transition matrix. The entries are in
percentages. The sum of each row must be equal to 100. For the bottom row,
which corresponds to the default state, the entries must all be 0 except for
the diagonal entry, which must be 100. |
|
time_points |
Time horizons at which default probabilities are to be
forecasted. In the functions aaCredit_DfltProb_DSSprd and aaCredit_ConvertDFtoDfltP,
it can be a single entry array of the value 0. For this case the time points will be
calculated from the input default swap maturities or from the dates of the
risk-free discount factor curve. |
|
asset_val |
Total asset value of a company |
|
vlt |
Volatility of the total asset |
|
debt |
Face value of a company's liabilities |
|
cost_hldg |
Pay out rate of a company - annual/365 |
|
rate_ann |
Risk free rate - annual/365 |
|
default_type |
A switch: 1 = default is checked only at the given time horizon (term),
|
|
term |
Time horizon to forecast default probability |
|
probordensity |
Probability or density - a switch |
|
prob_crv_ent3 |
Projected probability curve. It has N +1 columns. The first column has time (in years). The time must be in increasing order and
positive. If probordensity =1, the other columns are the default
probabilities of N reference entities up to the given time; otherwise, they
are the density values of a probability curves at the time period between the
given time and the previous time point in the curve. A probability curve must be non-decreasing
and not exceeding 1. A density curve
must be non-negative and its integral over the time periods of the curve must
not exceed 1. |
|
corr_mat_ent3 |
An N by N credit index correlation matrix with N the
number of reference entities |
|
prob_crv_ent2 |
A 3-column probability curve |
|
prob_crv |
A 2-column probability curve |
|
corr |
Credit index correlation |
|
num_rnd |
Number of random trials |
|
table_type |
Output table type. It
is used in aaCredit_DfltFirst_ind
and aaCredit_DfltFirst_MC. If table_type
=1, the output is a first-to-default probability curve table for all
reference entities; if table_type
=2, the output is a first-to-default density curve table; otherwise, it is
the default probability and density curve table for the basket of reference
entities. |
|
spread_tbl |
Used in aaCredit_DfltProb_DSSprd. Par credit default spread table. It is a five-column table: (effective date
of a default swap, terminating date, par spread, type of accrued interest
payment, recovery rate). The
terminating date must be in increasing order. The type of accrued interest payment takes
two values: 1 = pay accrued interest of premium upon default, 2 = pay no accrued interest of premium up on default. |
|
freq_prem |
Premium payment frequency |
|
acc |
Accrual method |
|
d_rul |
Business date convention |
|
intrp_prob |
Interpolation method of a probability curve: 1 = linear, 2 = exponential |
|
rate_recover |
A one-entry table of a recovery rate. |
|
acc_time |
Time accrual method |
|
min_years |
Minimum length (number of years) of the curve. It is used only when it is longer than the
length of the risk-free curve. |
|
calc_type |
Calculation method. It is not used in this release. |
|
df_crv_risk |
A risky discount factor curve. It is equivalent to a risky swap rate curve. |
|
adj_eff |
CDS effective
date adjustment, a switch (1 = adjust effective date, 2 = do not adjust
effective date). It is used in aaCredit_DfltProb_DSSprd3 only. |
|
adj_term |
CDS terminating
date adjustment, a switch (1 = adjust terminating date, 2 = do not adjust
terminating date). It is used in aaCredit_DfltProb_DSSprd3 only. |
|
dGen_method |
CDS date
generation method, a switch (1 = backward generation from the maturity date,
2 = forward generation from the effective date, 3 = IMM dates). An IMM date
is the 20th of a month. For example, if the coupon frequency is quarterly,
the IMM dates are March 20th, June 20th, September 20th
and December 20th. When the IMM method is selected, the maturity
date of a CDS will be moved to the next IMM date internally in the function.
Note also that IMM dates are generated backward from the maturity date. This
switch is used in aaCredit_DfltProb_DSSprd3 only. |
|
spred_tbl |
Used in aaCredit_DfltProb_DSSprd2.
, it is a eight-column table:
(effective date of a default swap,
terminating date, frequency, par spread, type of accrued interest payment,
payoff type, recovery rate, use this point). The terminating date must be in increasing
order. The type of accrued interest
payment takes two values: 1 = pay accrued interest of premium upon default, 2 = pay no accrued interest of premium up on default. |
|
cds_sprd_tbl |
Used in aaCredit_DfltProb_DSSprd3 and aaCredit_DfltProb_DSSprd_std. Par
credit default spread table. For aaCredit_DfltProb_DSSprd3, A CDS spread curve can be time-based (values in
the first column >0 and <1000) or date-based (values in the first
column >=1000). If it is time-based, the first column has CDS times to
maturity (in years). If it is date-based, it can have one (first) column CDS
(terminating) dates or two (first two) column CDS (effective, terminating)
dates. Times and terminating dates must be increasing and CDS spreads must be
nonnegative. If the table has two columns of dates, the effective date must
be prior to the terminating date, the
effective date of the first row must be prior to the valuation date d_v and that
of the ith row must be prior to
the terminating date of the (i-1)th row. The remaining
columns (see the CDS spread table definition) are the same for all the three
types of CDS spread tables. The last column, which is optional, has upfront
fees (as a % of notional). Excel users may pass term strings to represent
time intervals. Term strings must be in the format kB, kD, kW, kM, or kY
where k is an integer and B, D, W, M and Y stands for market day, calendar
day, week, month and year respectively, e.g., 3M = 3 months. For aaCredit_DfltProb_DSSprd_std, it is a six-column table: (maturity date of a default swap, frequency,
par spread, type of accrued interest payment, recovery rate, upfront
payment). These columns follow the
same restrictions and conventions mentioned above. |
|
method_boot |
The method of bootstrapping a default probability curve
from a par credit default spread curve, a switch: 1 = assuming a constant default density within two
consecutive time points of the credit spread curve; 2 = assuming a constant hazard rate within two consecutive
time points of the credit spread curve; 3 = interpolating the input credit spread curve to obtain
credit spreads on all coupon payment time points. For aaCredit_DfltProb_DSSprd3 and aaCredit_DfltProb_DSSprd_std,
only the first two methods are available. |
|
error_treat |
The error handling method for inconsistent input credit
spread curve, a switch: 1 = build a probability curve with part of the credit
spreads; 2 = output an error. Some input credit spread curves have consistent problems
such that it is impossible to build a default probability curve that will
value the given CDS', approximately, to the given spreads. For example, the input data may result in
negative default probabilities. However,
oftentimes, part of the input data is good and can be used to build a good
but short default probability curve. By
extrapolating such a short curve one can always build a default probability
curve that can cover the given time periods in the input data table. If a user does not want such an extrapolated
curve, he or she can use the switch value 2 that will lead to an output of an
error symbol. |
|
output_type |
In the functions aaCredit_DfltProb_DSSprd2
and aaCredit_DfltProb_DSSprd_std,
it is the output type of a default probability curve, a switch.
In this release, only one type, a
time-based default probability curve, is implemented. In the function aaCredit_convert_hazard,
it is the type of the output. It is a switch
with two values: 1 = a hazard rate curve; 2 = a default probability curve. |
|
mat_type |
CDS date generation method, a switch (1 = backward
generation, 2 = IMM date generation). It is used in aaCredit_DfltProb_DSSprd_std only. |
|
Hazardorprob |
Type of an input curve (used in the function) aaCredit_convert_hazard)
a switch: 1 = a hazard rate curve; 2 = a default probability curve. The input table can be a hazard curve or a default
probability curve for a single name or multiple names. |
Description of Outputs
All functions mentioned above, except for the functions aaCredit_DfltBarrier_MC2,
aaCredit_DfltCorr_MC,
aaCredit_ConvertDfltPtoDF,
aaCredit_convert_hazard, and aaCredit_Interp_DfltProb and aaCredit_Interp_DfltProb2,
outputs either a single-entity default probability curve or a basket default
probability curve. A single-entity
default probability curve is a two-column array (time in years, default
probability). A basket default
probability curve is a multi-column array (time in years, default probability
of entity i, i=1, 2, …, N). All output
default probability curves are time-based and hence each is associated with a
day-counting rule, also called a time-accrual method in the FINCAD math library.
The following table displays the type of
a default probability curve and its time-accrual method for each of the output
default probability curves.
|
Function |
type (1 = single, N =
basket) |
day counting rule |
|
1 |
30/360 |
|
|
1 |
30/360 |
|
|
1 |
act/365 |
|
|
1 |
acc (the input CDS accrual method) |
|
|
1 |
acc (the input CDS accrual method) |
|
|
1 |
acc (the input CDS accrual method) |
|
|
1 |
the same as the one of the input curve |
|
|
1 |
the same as the one of the input curve |
|
|
1 |
the same as the one of the input curve |
|
|
1 |
the same as the one of the input curve |
|
|
1 |
the same as the one of the input curve |
|
|
1 |
the same as the one of the input curve |
Remark 1: The day-counting rule is always part
of an output default probability curve. When such a default probability curve
is used as an input of a credit derivative valuation function, e.g., aaCDS,
and if its time-accrual method is not 30/360, the time-accrual method must also
be used as an input of the function. In
the newly added credit derivatives functions in the FINCAD XL version 9, the time-accrual
method should be put in the third entry of a default probability curve
interpolation/curve building array intrp_tb. For the other credit derivatives functions it
should be put at the upper right corner of a default probability curve.
Remark 2: The functions aaCredit_DfltProb_DSSprd3,
aaCredit_DfltProb_DSSprd2 and aaCredit_DfltProb_DSSprd_std build
default probability curves from a credit default swap spread curve. If one wants to use an output default
probability curve as an input to revalue the input credit default swaps and
check if the calculated credit default swap spreads match the original spreads,
the input time points array time_points must be a single-entry array with a
value of 0 and the time-accrual method of
the default probability curve must be set as the input credit default swap
accrual method which is used to build the default probability curve.
Remark 3: In aaCredit_DfltProb_DSSprd2 when the bootstrapping method is set
to 3 (interpolate CDS spread curve) and if the time points array is a
single-entry array with a value of 0, the time points of the output default
probability curve is determined by all of the coupon payment dates of the
credit default swaps in the input credit default swap spread array. Generally, the output default probability curve
has more rows than the input default spread curve.
This function
calculates the default barriers of a standard credit index process at multiple
time points. Its output is a two-column
array (time in years, default barrier). The
results are used in the calculation of nth-to-default default probabilities,
when the reference credits in a basket are correlated and when the so-called
multi-step credit index model (
This function outputs a three-column table (time
in years, the probability that both reference credits default, default correlation). Note that both the joint default
probabilities and the default correlation are time-dependent.
The output is a
two-column discount factor curve.
The output is either a basket default probability curve if the input
curve is a basket hazard rate curve, or a basket hazard rate curve if the input
curve is a basket default probability curve. In both cases the day counting rule is the
same as the one in the input curve.
It outputs a three column table (time in years, default probability,
default density). The day counting rule
is the same as the one in the input curve.