Credit Default Index Swaps (CDS Indices)

Overview

A credit default index swap (CDIS) is a credit default swap (CDS) on a portfolio of entities, or more specifically, a portfolio of single entity CDSs. It can be seen as an extension of a CDS on a single entity to a portfolio of entities (for single entity CDSs see the Credit Default Swaps FINCAD Math Reference document). Like a single entity CDS, it has a payoff leg (also known as a default leg, a protection leg or a floating leg), and a premium leg that has a fixed coupon rate. The basic difference is that in a CDS the notional is fixed during the life of the CDS and the protection buyer is compensated at most once, while in a CDIS the premium notional is variable. Whenever a default in the portfolio occurs, the protection buyer gets compensated by the lost amount and the CDIS continues with its premium notional being reduced by the lost amount of the defaulted entity. The most popular CDISs are the so-called standardized CDISs. In these standardized contracts the reference entity pool is homogeneous, that is, all the reference entities have the same notional and the same recovery rate. Typical examples of standardized CDISs are the CDX index and the ITRAXX index.

FINCAD provides tools to calculate fair values and risk statistics of CDISs. FINCAD also provides tools to value two other types of CDS index-based credit derivatives, CDIS options and standardized CDO tranches. For details on these types of credit derivatives, see the Credit Default Index Swap Options and Synthetic CDO Valuation Using Quasi-Analytic Methods FINCAD Math Reference documents.

Formulas & Technical Details

Suppose that we want to value a portfolio of n single entity CDSs. For each single entity CDS , let denote the value of the payoff leg and that of the premium leg with a premium coupon rate of 100%. The value of the payoff leg of the index is the sum of the individual payoff values of the index:

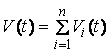
and the value of the premium leg of the index is the sum of the individual premium leg values:

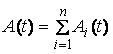
Thus the fair value of the CDIS is:

where is the premium coupon rate, i.e., the deal spread.

The fair spread of the CDIS can then be calculated as:

which can be viewed as a weighted average of the individual CDS spreads:

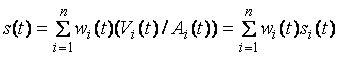
where

and

is the par spread of CDS

Calculation of Risk Statistics

DVOX

DVOX of a CDIS is defined as the change in the fair value per basis point shift in all the par CDS spread curves of the entities in the reference pool. In more detail, let be the fair value of a CDIS. For every entity in the reference pool, add basis points to its default curve (if it is a default probability curve, derive a par spread curve first) and build a new default curve. Then combine these default curves together to form a basket default curve and at last use this basket default curve as an input to revalue the CDIS. Let be the new fair value. The DVOX is then calculated as follows:

Rho of recovery rate

Rho of recovery rate of a CDIS is the change in the fair value of a CDS per 1% change in the recovery rate. In more detail, let be the fair value of the CDIS when the entity’s recovery rate is . Then:

If the recovery rates of the reference entities differ, the recovery rate in the above formula should be replaced with a recovery rate vector and to bump it we simply add 0.01 to every component of the vector.

Theta

The theta of a CDIS is the change in the fair value of the CDIS per one day increase of the valuation date. Let be the fair value of the CDIS. Then:

BPV

The BPV (basis point value) of a risk free discount factor curve is the change in the fair value of a CDIS when the risk-free discount factor curve is shifted up one basis point. To shift up a discount factor curve simply add one basis point to every point of the corresponding spot rate curve of the discount factor curve.

FINCAD Functions

aaCDS_index(d_v, contra_d, cpn_pr, freq_pr, pr_acc_type, acc, d_rul, ref_type, ref_bskt, dp_type, dp_bskt, intrp_tb, hl, dfstd, intrp, pos, calc_para, stat)

Calculates the fair value, payoff, par spread and other statistics of a credit default swap index. The default estimation data can be par CDS spread curves or default probability curves.

aaCDS_index_is(d_v, contra_d, cpn_pr, freq_pr, pr_acc_type, acc, d_rul, cds_p, ref_type, ref_bskt, dp_type, dp_bskt, intrp_tb, hl, dfstd, intrp, calc_type):

Calculates the implied spread of a credit default index swap given a price.

aaCDS_index_std(d_v, contra_d, ref_npa, num_ref_ini, num_dflt, loss_cum, npa_CDS, cpn_pr, freq_pr, acc, d_rul, dp_type, dp_bskt, intrp_tb, rate_recover, hl, dfstd, intrp, pos, calc_para, stat)

Calculates the fair value, payoff, par spread and other statistics of a standardized credit default index swap.

aaCDS_index_std_is(d_v, contra_d, ref_npa, num_ref_ini, num_dflt, loss_cum, npa_CDS, cpn_pr, freq_pr, acc, d_rul, cds_p, dp_type, dp_bskt, intrp_tb, rate_recover, hl, dfstd, intrp, calc_type):

Calculates the implied spread of a standardized credit default index swap given a price.

Description of Inputs

Input Argument	Description
d_v	Valuation date
contra_d	Contra_d is a table of default swap date(s). It can have 2 to 7entriese. The first four entries hold in sequence the terminating date, effective date, odd first coupon date and next-to-terminating coupon date for premium payments. The last three entries hold switch values in sequence the effective date adjustment, terminating date adjustment and date generation method for premium payments. Only the terminating date and effective date are required. The third entry and fourth entry default to 0 and the last three entries will default to 1: adjust effective date, adjust maturity date, backward date generation, respectively. Note that for most credit default index swaps in the market, the effective date and terminating date are not adjusted and the premium cash flow dates are IMM dates. For this case, simply set both the effective date and terminating date adjustment methods (the 5^th and 6^th entries in the table) to 2 (no adjustment) and the date generation method (the 7^th entry in the table) to 3 (IMM dates).
ref_npa	Notional of a reference entity
num_ref_ini	Number of reference entities in the initial pool
num_dflt	Number of defaulted reference entities
loss_cum	Accumulated loss of the pool (if 0, will be calculated from the defaulted credits)
npa_CDS	CDS notional (if 0, will be calculated as the total notional of the pool)
cpn_pr	Premium payment rate
freq_pr	Premium payment frequency - a switch
pr_acc_type	Type of premium accrued interest payments. – a switch 1 = pay accrued interest of premium upon default, 2 = pay no accrued interest of premium upon default
acc	Accrual method of premium – a switch
d_rul	Business date convention for premium payment - a switch
ref_type	Reference type – a switch: 1 = name table, 2 = bond table
ref_bskt	Reference basket table. If the reference type ref_type =1, it is a two-column table (notional, recovery rate) as shown in the following examples. If the reference type ref_type =2, the reference data table has the details of a bond. It can be a 10-. or 11-entry table. The first 10 entries are (principal, maturity, dated date, first coupon date, next-to-last coupon date, coupon, frequency, accrual method, business day convention, recovery rate). See aaBond3 for their definitions. If it has 10 entries only, the last entry has the recovery rate for both principal and coupon of the bond. If it has 11 entries, the 10th and 11th entries have principal and coupon recovery rates respectively.
dp_type	Curve type – a switch: 1 = par CDS spread curve, 2 = default probability curve
dp_bskt	dp_bskt is a default curve. If the default curve type dp_type = 1, the default curve dp_bskt is a par CDS spread curve. It can be date-based or time-based. If the first entry in the first row of the first column is <1000, it is a time-based curve; otherwise it is date-based. For a date-based curve, it has m+2 columns, where m is equal to one or the number of rows in the reference basket (ref_bskt). The first two columns are effective date and terminating date. For a time-based curve, it has m+1 columns. The first column has times in years (>0 and ascending). In both cases, the last m columns are the par CDS spreads of references in the basket, respectively. If the default curve type dp_type =2, the default curve dp_bskt is a default probability curve. In this case, the first column can be times (in years) or dates and all other columns are default probability values; time and date must be non-decreasing; for a date based curve, the first date must be equal to a valuation date if there is one and default probability values in the first row should be zero. When m is equal to one, all the reference credits have the same curve.
intrp_tb	The array intrp_tb can have one to six entries. The first entry has the default probability curve interpolation method. The second entry has the default probability curve bootstrapping method (see switch sw_1040 in aaCredit_dfltprob_DSSpred2). It is used only if the default curve type is "par CDS spread curve" ( dp_type =1). If this entry is missing and dp_type=1, the bootstrapping method will be set to method 1 (assuming constant default density). The third entry stores the time accrual (day counting) method if the default curve is time-based. If this entry is missing and the default curve is time-based, the time accrual method will be set to 30/360. If the default curve is not time based, this entry will be ignored. The fourth to sixth entries store the effective and terminating date adjustment methods and the date generation method of a CDS curve, respectively. These entries are used only when dp_type = 1. Their default values are 1.
rate_recover	Recovery rate
hl	A holiday list
dfstd	Risk-free discounting factor curve or a risk-free yield. The discount factor curve may be input as a 2-column, multi-row table (col 1 = date, col 2 = discount factor), or as a single cell containing a rate. If input as a single rate, there are three format choices: 1. a rate (1 row, 1 column); or 2. a rate and a rate quotation basis (1 row, 2 columns); or 3. a rate, a rate quotation basis, and an accrual method (1 row, 3 columns). If the basis or accrual are not provided, they are assumed to be annual, actual/365. A 2-column flat-rate discount factor curve is constructed internally using the rate, basis, and accrual method. The last date in the discount factor curve >= last "date" in the default curve and the terminating date of the swap.
intrp	Interpolation method of the discount factor curve
pos	Trading position - a switch: 1 = pay premium, 2 = receive premium.
calc_para	The table calc_para can have 1 or 2 entries. The first entry is a calculation method used in CDS valuation (see switch sw_624 in the function aaCDS). The optional second entry is the number of basis points used in DVOX calculation; it is defaulted to 1 when missing. Caution: Negative values of the second entry can cause the function to fail.
stat	Output statistics

Note: Reference table ref_bskt of aaCDS_index assumes that only non-defaulted reference entities are listed in the table.

Description of Outputs

For the functions that calculate fair value and risk statistics, the outputs are:

Output Statistic	Description
1	fair value: fair value of a default swap (= payoff – premium )
2	value of payoff
3	value of premium
4	accrued interest of premium
5	fair value minus accrued interest
6	par spread: premium rate that makes the CDIS have a fair value - accrued interest of 0.
7	basis point value of risk-free curve: change of the CDIS fair value per one basis up shift of the risk-free discount factor curve
8	number of days that premium accrues
9	next premium payment date
10	previous premium payment date
11	Number of remaining cash flows
12	DVOX of par CDS spread curve: change of the CDIS fair value per X basis points up shift of the par CDS spread curve.
13	rho of recovery rate: change of the CDIS fair value per 1% increase of the recovery rates.
14	theta: change of the CDIS fair value per one day increase of valuation date.

aaCDS_index_std has two more statistics:

Output Statistic	Description
15	accumulated loss
16	outstanding notional

Functions aaCDS_index_is and aaCDS_index_std_is have only a single output: implied spread given price. It is the CDIS premium rate that makes the fair value minus accrued interest (the fifth output statistic of aaCDS_index or aaCDS_index_std) equal the given price.

Examples

Example 1

Suppose a CDIS index consists of three reference entities. Each reference entity has different notional, credit spread curve and recovery rate as described in the following tables. The CDS index started on Jun. 1, 2005 and matures on Dec.1, 2008. To seek for protection on the reference pool, a company bought a CDIS on this index. The company will pay a 2% premium quarterly. Suppose that today’s date is Dec. 1, 2005, and there are no defaulted reference entities so far. Other details of the CDIS required for valuation are given in the following tables. For simplicity, holidays are ignored.

aaCDS_index

Argument	Description	Example Data	Switch
d_v	Valuation date	1-Dec-2005
contra_d	CDS contract dates	see below
cpn_pr	Premium payment rate	2%
freq_pr	Premium payment frequency	3	quarterly
pr_acc_type	Type of premium accrued interest payments.	1	pay accrued interest upon default
acc	Accrual method of premium	2	actual/360
d_rul	Business date convention for premium payment	2	next business date
ref_type	Reference type	1	name(notional recovery)
ref_bskt	Reference basket table	see below
dp_type	Default curve type	1	par CDS spread curve
dp_bskt	Basket default curve	see below
intrp_tb	Default curve parameter table	see below
hl	A holiday list	see below
dfstd	discount factor curve	see below
intrp	Interpolation method of the discount factor curve	1	Linear
pos	Trading position	1	Long
calc_para	Calculation parameters	see below
stat	Statistics	{1,2,…,14}

contra_d: CDS contract dates

Terminating date	Effective date	First coupon date	Next to last coupon date	Effective date adjustment	Terminating date adjustment	Date generation method
20-Dec-08	1-Dec-04	0	0	2	2	3
				switch: do not adjust effective date	switch: do not adjust terminating date	switch: IMM

ref_bskt: reference basket table

Notional Amount	Recovery Rate
1000000	40.000%
2000000	50.000%
1000000	45.000%

dp_bskt: basket default curve

Time (in years)	CDS Spread of Credit 1	CDS Spread of Credit 2	CDS Spread of Credit 3
0.5	0.0009	0.0011	0.001
1	0.001	0.0013	0.0011
2	0.0019	0.0021	0.002
3	0.0027	0.0031	0.0027
4	0.0035	0.0038	0.0037
5	0.0044	0.005	0.0046
7	0.0054	0.006	0.0056
10	0.0066	0.007	0.0068

intrp-tb: interpolation/probability curve building parameters

Interpolation of Default Probability Curve	Bootstrapping Method	Accrual Method	Effective date adjustment	Terminating date adjustment	Date generation method
1	1	4	2	2	3

hl: holiday list

Holiday Date

25-Dec-2004

1-Jan-2005

25-Dec-2005

1-Jan-2006

25-Dec-2006

1-Jan-2007

25-Dec-2007

1-Jan-2008

25-Dec-2008

1-Jan-2009

25-Dec-2009

1-Jan-2010

dfstd: discount factor curve – risk free

Grid Date	Discount Factor
1-Dec-2005	1
1-Jun-2006	0.971285862
1-Dec-2006	0.943396226
1-Dec-2007	0.88999644
1-Dec-2008	0.839619283
1-Dec-2010	0.747258173
1-Dec-2015	0.558394777
1-Dec-2020	0.417265061

calc_para: calculation parameters

Calculation Method	Bump Size for DVOX (in basis points)
1	1

To value this CDIS, call the FINCAD function aaCDS_index to get the following results:

Results

Statistics	Description	Value
1	fair value	-207525.866018
2	value of payoff	32487.141234
3	value of premium	-240013.007251
4	accrued interest of premium	-16000.000000
5	fair value minus accrued interest	-191525.866018
6	par spread	0.002900
7	basis point value of risk-free curve	29.337025
8	number of days that premium accrues	72.000000
9	next cash flow date	38706.000000
10	previous cash flow date	38615.000000
11	number of remaining cash flows	13.000000
12	DVOX of par CDS spread curve	1173.688816
13	rho of recovery rate	21.975129
14	Theta	-66.610822

Note that the spread 0.002900 calculated above is the par spread of the CDSI. This spread values the fair value minus the accrued interest to 0. Suppose one wants to find out the implied spread that values the fair value minus the accrued interest to 10000. Then one can simply call function aaCDS_index_is with the data given in the above input data table and the CDIS price. The following is the result of the function call:

Result

implied spread

0.002007664

As an exercise it is easy to check that if the CDIS price is replaced with the output fair value minus accrued interest (the fifth statistic) given above in the function call to aaCDS_index_is, the output implied spread will be 2%, which is exactly the input premium coupon rate, as is expected.

Example 2

Suppose the data of a CDS index is the same as in Example 1 except that there are 125 reference entities and all the reference entities have the same notional, recovery rate and credit spread curve of the first reference entity of Example 1. Suppose two reference entities have defaulted. To value the CDIS call the FINCAD function aaCDS_index_std with the following inputs:

aaCDS_index_std

Argument	Description	Example Data	Switch
d_v	Valuation date	1-Dec-2005
contra_d	CDS contract dates	see above
ref_npa	Notional of a reference entity	1,000,000
num_ref_ini	Number of reference entities in the initial pool	125
num_dflt	Number of defaulted reference entities	2
loss_cum	Accumulated loss of the pool (if 0, will be calculated from the defaulted credits)	0
npa_CDS	CDS notional (if 0, will be calculated as the total notional of the pool)	0
cpn_pr	Premium payment rate	0.02
freq_pr	Premium payment frequency	3	quarterly
acc	Accrual method of premium	2	actual/360
d_rul	Business date convention for premium payment	2	next business day
dp_type	Default curve type	1	par CDS spread curve
dp_bskt	basket default curve	see above
intrp_tb	Default curve parameter table	see above
rate_recover	Recovery rate	0.4
hl	A holiday list	see above
df_crv_std	discount factor curve – risk free	see above
intrp	Interpolation method of the discount factor curve	1	linear
pos	Trading position	1	long
calc_para	calculation parameters	see above
stat	Statistics	{1,2,…,16}

The results (aaCDS_index_std) are shown below:

Results

Statistics	Description	Value
1	fair value	-6498651
2	value of payoff	937186.41
3	value of premium	-7435837
4	accrued interest of premium	-495200
5	fair value minus accrued interest	-6003451
6	par spread	0.0027006
7	basis point value of risk-free curve	919.81852
8	number of days that premium accrues	72
9	next cash flow date	38706
10	previous cash flow date	38615
11	number of remaining cash flows	13
12	DVOX of par CDS spread curve	36203.102
13	rho of recovery rate	498.78714
14	Theta	-1995.374
15	accumulated loss	1200000
16	outstanding notional	123800000

Related Functions

CDIS functions use CDS functions to calculate fair value, payoff and premium values and risk statistics of a CDIS. The closest related CDS function is aaCDS and aaCDS_is.

References

[1] Amato, J. D. and Gyntelberg, J., (March 2005), ‘CDS Index Tranches and the Pricing of Credit Risk Correlations’, BIS Quarterly Review, part 7, p. 73-87.

[2] Hull, J. and White, A., (Fall 2000), ‘Valuing Credit Default Swaps I, No Counterparty Default Risk’, The Journal of Derivatives, 8 (1), p. 29-40.

Disclaimer

With respect to this document, FinancialCAD Corporation (“FINCAD”) makes no warranty either express or implied, including, but not limited to, any implied warranty of merchantability or fitness for a particular purpose. In no event shall FINCAD be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of the use of this document or the information contained in it. This document should not be relied on as a substitute for your own independent research or the advice of your professional financial, accounting or other advisors.

This information is subject to change without notice. FINCAD assumes no responsibility for any errors in this document or their consequences and reserves the right to make changes to this document without notice.