Interest Rate Caps and Floors
Overview
Description
A rate cap is an agreement between two parties providing
the purchaser an interest rate ceiling or ‘cap’. This financial instrument is primarily used
by borrowers of floating rate debt in situations where short term interest
rates are expected to increase. For
highly leveraged companies or those with an overweighting of short term debt,
rate caps are used to manage interest expense and therefore, the profitability
profile of the organization. Rate caps can thus be viewed as insurance,
ensuring that the maximum borrowing rate never exceeds the specified cap
level. In exchange for this peace of
mind, the purchaser pays the financial institution a premium.
An interest rate floor on the other hand, guarantees a
lower bound for the rate of interest received on an investment. This may be used in conjunction with a
floating rate note (FRN) to ensure a minimum return on investment. Sometimes these rate guarantees are embedded
into financial instruments such as structured medium term notes. Floors are used in times of decreasing short
term interest rates by money managers trying to obtain higher cash returns on
floating rate investments. Naturally,
compensation is paid to the seller in return for the interest rate guarantee.
Formulas & Technical Details
Valuation and Risk Measures
Rate Caps – Black Model
The basic model for rate caps or floors is as described in
Let
be the cap
rate,
be the time
from the valuation date until the start of the caplet,
be the
length of the caplet period (from to 
) and
be the
(unknown) reset rate for the caplet at time .
As previously defined the cash flow for the caplet period
is 
, at time ,
or a value of 
at time . Thus, the
pay-out for the caplet looks much like the pay-out from a European option
terminating at time and a commonly
used valuation model treats it as such.
Clearly, at the valuation date, one does not know the
reset rate . One only has
the implied forward rate 
. In the basic
valuation a simplification is made.
Letting 
be the discount
factor from time to , one assumes that the value at time is 
. Now is treated as a
stochastic term while the rest of the terms are held fixed, including 
(though it depends on ). Assuming has a lognormal
distribution (with a constant volatility 
), one may model the caplet as a European call option
on the forward rate using the Black
model.
Consider the Black model with a forward rate of , a strike of , a volatility , an option period of and a risk-free
interest rate of 
(compounded
continuously). The fair value of a call
option is:
where
and 
( . ) is the
cumulative standard normal distribution.
Note that 
is simply the
discount factor that applies on the option expiry date. This can be obtained directly from the zero
curve and is replaced
with 
. Hence, for
the caplet, one applies the Black model with a forward rate of , a strike of , a volatility , an option
period of and a discount
factor of . The
fair-value in dollars for the caplet is then:
fair value: 
delta: 
gamma: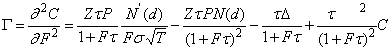 
vega: 
Consider the Greeks for this caplet. As shown, delta is in units of currency per
100% change in the implied forward rate.
To convert this to currency per bp, simply divide by 10000. To convert gamma to units of currency per bp2,
divide the gamma above by 100002.
Vega is in units of currency per 100% change which can be converted to
currency per 1% change by dividing by 100.
The final statistic is theta.
The dollar-based theta is the sum of two terms. The first term is the rate-based theta from
the Black model multiplied by the dollar conversion factor 
. The second term is
the dollar price of the option, 
, multiplied by the continuously compounded forward rate from
the valuation date to the maturity of the caplet. This second term arises from
the derivative of the discount factor 
with respect to
time , and is an approximation since the discount factor
curve is given at discrete points. Theta has units of currency per day.
In the standard Black model, there is no extra term
required for the discounting of a cash flow from the maturity date of the
caplet () to the expiration date of the option (the term 
). Hence, a more standard approach defines:
delta: 
gamma: 
These are obtained by differentiation with
respect to the forward rate ignoring the extra terms arising from the differentiation
of the term . In any usual
circumstance there is little difference between the different deltas and
gammas. The FINCAD functions return these
more standard versions of delta and gamma.
In the valuation formula, we multiply the bracketed term
by a scaling factor 
. If you bring
this factor inside the brackets, you obtain exactly the same answer for the
caplet by replacing and in the option
model with the present value of the cash flows when using and respectively.
Also note that and can be
independent of the zero curve used to discount cash flows. For example, in a constant maturity cap(let)
the forward rate that applies
for a particular period , may be the ten year constant maturity
treasury rate as at time . This value
would be derived from a separate treasury curve and would be used to calculate
the appropriate cash flow. Any
discounting, however, would most likely be done using the standard Libor curve.
Rate Floors – Black Model
A rate floor is simply modeled as a European Put on the
forward rate with all other assumptions as described above for caps. One applies the Black model for a put with a
forward rate of , a strike of 
, a volatility and an option expiry
of .
The remaining details for rate floors carry through much
as above, giving:
fair value: 
delta: 
gamma:
vega: 
Theta is calculated as it was for rate caps.
FINCAD Functions
The FINCAD library contains several functions to value
European-style Rate Caps and Rate Floors and can be classified by the type of
underlying model used to derive the fair value and other statistics.
The functions aaCaplet_BL, aaRcap_BL,
aaRcap_BL_p, aaRcap_BL_iv, aaRcap_BL_dgen, aaRcap_BL_dgen_p, and aaRcap_BL_dgen_iv
use the Black model. The seven _BL*
functions allow for:
·
option expiry prior to the caplet/floorlet
effective date;
·
a multiplying factor for the forward and reset
rates, whereby the rates are multiplied by 75% (for example) before use. This feature may be used to define tax–exempt
instruments.
The functions aaRcap_BL, aaRcap_BL_p,
and aaRcap_BL_iv
take caplet tables, which allow custom structures to be defined. The function aaRcap_BL_iv calculates
the “volatility spread” – the spread that would give the target price for the
cap if the volatility of each caplet were increased by that amount.
The functions aaRcap_BL_dgen,
aaRcap_BL_dgen_p, and aaRcap_BL_dgen_iv first
generate the caplet/floorlet dates at a specified frequency. For each caplet, the volatility is then taken
from the last row in the supplied volatility table whose date is equal or prior
to the maturity of the particular caplet.
Likewise, the reset rate is taken from the last row in the supplied
reset table whose date is equal or prior to the reset date of the particular
caplet. The function aaRcap_BL_dgen_iv
calculates the “flat volatility” – the volatility that would give
the target price if all caplets had that same volatility.
There are eight functions for digital caps and floors
using the Black model. The payoff of
these instruments is a set cash amount if the rate is below (or above) the
exercise rate for the cap (or floor) and zero otherwise. The functions aaCaplet_digital_BL,
aaRcap_digital_BL, aaRcap_digital_BL_p, aaRcap_digital_BL_iv,
aaRcap_digital_BL_dgen, aaRcap_digital_BL_dgen_p, and aaRcap_digital_BL_dgen_iv
are used in a similar fashion as the regular cap/floor functions with almost
identical input parameters. The only
difference is that what was once the principal amount for the regular caplets
is now the (annualized) cash payout amount for the digital caplets. An additional function, aaRcap_digital_BL_dgen_tables,
is included that generates a caplet table for digital caps with dates at a
specified frequency that can be used by the aaRcap_digital_BL* functions.
There are also eight functions for CMS/CMT style caps and
floors using the Black model. These
functions are: aaCaplet_CM_BL,
aaRcap_CM_BL, aaRcap_CM_BL_p, aaRcap_CM_BL_iv, aaRcap_CM_BL_dgen_tables,
aaRcap_CM_BL_dgen, aaRcap_CM_BL_dgen_p and aaRcap_CM_BL_dgen_iv. For more information on these functions, see
the Constant Maturity Derivatives
FINCAD Math Reference document.
The functions aaRcap_BK and aaCaplet_BK
calculate fair value based on the Black-Karasinski or Lognormal one-factor
short rate model; and the functions aaRcap_HW and aaCaplet_HW
calculate fair value based on the Hull-White or Ho-Lee one-factor short rate model.
Note that the Hull-White model for the pricing of European-style caps/floors is
solved in a closed form iterative process.
The functions aaRcap_MF and aaCaplet_MF
calculate fair value based on the Hull-White
or Additive Gaussian two-factor short rate model (Multi-Factor Short Rate Models
FINCAD Math Reference document). The
functions aaCaplet_LMM
and aaCapletVltGen_LMM
calculate fair value and Black volatility based on a
parameterization of the Libor Market Model
(FINCAD Math Reference document).
The function aaRCapAsian uses
an Asian option model to calculate the fair value and risk statistics for a
cap/floor in which the reset frequency is greater than the caplet frequency,
and each caplet payoff is based upon an arithmetic average of the reset rates
in the caplet period. For more details
see the Interest Rate Caps & Floors (Average)
FINCAD Math Reference document.
aaCaplet_BL(r_option_type, npa, d_v, d_exp, d_e, d_t,
capsettle, rate_reset, scale_rate, rate_ex, acc_rt, acc_pay, vlt, df_crv_acc,
df_crv_disc, intrp, stat)
Calculates fair
value and risk statistics for a caplet or floorlet using the Black model.
aaRcap_BL(d_v, caplet_tbl, r_option_type, capsettle,
scale_rate, acc_rt, acc_pay, df_crv_acc, df_crv_disc, intrp)
Calculates a caplet/floorlet information table that
includes fair value and risk statistics for a user-defined cap/floor using the
Black model.
aaRcap_BL_p(d_v, caplet_tbl, r_option_type, capsettle,
scale_rate, acc_rt, acc_pay, df_crv_acc, df_crv_disc, intrp, stat)
Calculates fair value and risk statistics for a
user-defined cap/floor using the Black model.
aaRcap_BL_iv(d_v, caplet_tbl, price, r_option_type,
capsettle, scale_rate, acc_rt, acc_pay, df_crv_acc, df_crv_disc, intrp)
Calculates implied volatility spread for a user-defined
cap/floor using the Black model.
aaRcap_BL_dgen(d_v, d_e, d_m, d_f_cpn, d_l_cpn, freq,
eff_mktdays, npa, rate_ex, vlt_crv, r_rate_obj, r_option_type, capsettle,
scale_rate, acc_rt, acc_pay, hl, d_rul, df_crv_acc, df_crv_disc, intrp)
Calculates a caplet/floorlet information table that
includes fair value and risk statistics for a generic cap/floor using the Black
model (dates generated).
aaRcap_BL_dgen_p(d_v, d_e, d_m, d_f_cpn, d_l_cpn, freq,
eff_mktdays, npa, rate_ex, vlt_crv, r_rate_obj, r_option_type, capsettle,
scale_rate, acc_rt, acc_pay, hl, d_rul, df_crv_acc, df_crv_disc, intrp, stat)
Calculates fair value and risk statistics for a generic
cap/floor using the Black model (dates generated).
aaRcap_BL_dgen_iv(d_v, d_e, d_m, d_f_cpn, d_l_cpn, freq,
eff_mktdays, npa, rate_ex, price, r_rate_obj, r_option_type, capsettle,
scale_rate, acc_rt, acc_pay, hl, d_rul, df_crv_acc, df_crv_disc, intrp)
Calculates flat volatility for a generic cap/floor using
the Black model (dates generated).
aaCaplet_digital_BL(r_option_type, payout, d_v, d_exp, d_e,
d_t, capsettle, rate_reset, scale_rate, rate_ex, acc_rt, acc_pay, vlt,
df_crv_acc, df_crv_disc, intrp, stat)
Calculates fair value and risk statistics for a digital
caplet or floorlet using the Black model.
aaRcap_digital_BL(d_v, caplet_tbl, r_option_type, capsettle,
scale_rate, acc_rt, acc_pay, df_crv_acc, df_crv_disc, intrp)
Calculates a caplet/floorlet information table that
includes fair value and risk statistics for a user-defined digital cap/floor
using the Black model.
aaRcap_digital_BL_p(d_v, caplet_tbl, r_option_type, capsettle,
scale_rate, acc_rt, acc_pay, df_crv_acc, df_crv_disc, intrp, stat)
Calculates fair value and risk statistics for a
user-defined digital cap/floor using the Black model.
aaRcap_digital_BL_iv(d_v, caplet_tbl, price, r_option_type,
capsettle, scale_rate, acc_rt, acc_pay, df_crv_acc, df_crv_disc, intrp)
Calculates implied volatility for a user-defined digital
cap/floor using the Black model.
aaRcap_digital_BL_dgen(d_v, d_e, d_m, d_f_cpn, d_l_cpn, freq,
eff_mktdays, payout, rate_ex, vlt_crv, r_rate_obj, r_option_type, capsettle,
scale_rate, acc_rt, acc_pay, hl, d_rul, df_crv_acc, df_crv_disc, intrp)
Calculates a caplet/floorlet information table that
includes the fair value and risk statistics for a generic digital cap/floor
using the Black model (dates generated).
aaRcap_digital_BL_dgen_p(d_v, d_e, d_m, d_f_cpn, d_l_cpn, freq,
eff_mktdays, payout, rate_ex, vlt_crv, r_rate_obj, r_option_type, capsettle,
scale_rate, acc_rt, acc_pay, hl, d_rul, df_crv_acc, df_crv_disc, intrp, stat)
Calculates fair value and risk statistics for a generic
digital cap/floor using the Black model (dates generated).
aaRcap_digital_BL_dgen_iv(d_v, d_e, d_m, d_f_cpn, d_l_cpn, freq,
eff_mktdays, payout, rate_ex, price, vlt_crv, r_rate_obj, r_option_type,
capsettle, scale_rate, acc_rt, acc_pay, hl, d_rul, df_crv_acc, df_crv_disc,
intrp)
Calculates implied volatility for a generic digital
cap/floor using the Black model (dates generated).
aaRcap_digital_BL_dgen_tables(d_v, d_e, d_m, d_f_cpn, d_l_cpn, freq,
eff_mktdays, payout, rate_ex, vlt_crv, r_rate_obj, r_option_type, capsettle,
scale_rate, acc_rt, acc_pay, hl, d_rul, df_crv_acc, df_crv_disc, intrp)
Generates digital caplet tables (used by
aaRcap_digital_BL) for a generic digital cap/floor using the Black model.
aaCaplet_CM_BL(r_option_type, npa, d_v, d_exp, d_e, d_t, paydate,
cm_reset, scalefactor, rate_ex, acc_pay, vlt_cm, vlt_fwd, corr_cm, d_cm_reset,
d_cm_e, freq_cm, numcf_cm_yld, acc_cm, d_rul_cm, hl, df_crv_acc, df_crv_disc,
intrp, stat)
Calculates fair value and risk statistics for a CMS caplet
or floorlet using the Black model.
aaRcap_CM_BL(d_v, CM_caplet_tbl, r_option_type,
scalefactor, acc_pay, freq_cm, numcf_cm_yld, acc_cm, d_rul_cm, hl, df_crv_acc,
df_crv_disc, method, intrp)
Calculates a caplet/floorlet information table that
includes fair value and risk statistics for a user-defined CMS cap/floor using
the Black model.
aaRcap_CM_BL_p(d_v, CM_caplet_tbl, r_option_type,
scalefactor, acc_pay, freq_cm, numcf_cm_yld, acc_cm, d_rul_cm, hl, df_crv_acc,
df_crv_disc, method, intrp, stat)
Calculates fair value and risk statistics for a
user-defined CMS cap/floor using the Black model.
aaRcap_CM_BL_iv(d_v, CM_caplet_tbl, price, r_option_type,
scalefactor, acc_pay, freq_cm, numcf_cm_yld, acc_cm, d_rul_cm, hl, df_crv_acc,
df_crv_disc, method, intrp)
Calculates implied volatility spread for a user-defined
CMS cap/floor using the Black model.
aaRcap_CM_BL_dgen(d_v, d_e, d_m, d_f_cpn, d_l_cpn, freq,
eff_mktdays, npa, rate_ex, vol_corr_tbl, r_table, r_option_type, set_pay,
scalefactor, acc_cm, acc_pay, hl, d_rul_pay, freq_cm, numcf_cm_yld, d_rul_cm,
df_crv_acc, df_crv_disc, method, intrp)
Calculates a caplet/floorlet information table that
includes fair value and risk statistics for a generic CMS cap/floor using the
Black model (dates generated).
aaRcap_CM_BL_dgen_p(d_v, d_e, d_m, d_f_cpn, d_l_cpn, freq,
eff_mktdays, npa, rate_ex, vol_corr_tbl, r_table, r_option_type, set_pay,
scalefactor, acc_cm, acc_pay, hl, d_rul_pay, freq_cm, numcf_cm_yld, d_rul_cm,
df_crv_acc, df_crv_disc, method, intrp, stat)
Calculates fair value and risk statistics for a generic
CMS cap/floor using the Black model (dates generated).
aaRcap_CM_BL_dgen_iv(d_v, d_e, d_m, d_f_cpn, d_l_cpn, freq,
eff_mktdays, npa, rate_ex, price, vol_corr_tbl, r_table, r_option_type,
set_pay, scalefactor, acc_cm, acc_pay, hl, d_rul_pay, freq_cm, numcf_cm_yld,
d_rul_cm, df_crv_acc, df_crv_disc, method, intrp)
Calculates implied volatility spread for a generic CMS
cap/floor using the Black model (dates generated).
aaRcap_CM_BL_dgen_tables(d_v, d_e, d_m, d_f_cpn, d_l_cpn, freq,
eff_mktdays, npa, rate_ex, vol_corr_tbl, r_table, r_option_type, set_pay,
scalefactor, acc_cm, acc_pay, hl, d_rul_pay, freq_cm, numcf_cm_yld, d_rul_cm,
df_crv_acc, df_crv_disc, method, intrp)
Generates CMS caplet tables (used by aaRcap_CM_BL) for a
generic CMS cap/floor using the Black model.
aaCaplet_BK(r_option_type, princ, d_v, d_exp, d_e, d_t,
rate_ex, acc, a, vlt_rate, df_crv, intrp, iter_year, stat)
Calculates fair value of a caplet or floorlet. The
Black-Karasinski (or Lognormal) term structure model is used.
aaRcap_BK(d_v, rcap2_obj, acc, df_crv, intrp, a,
vlt_rate, iter_year)
Calculates the fair value and the implied forward rate for
a table of caplets or floorlets. The Black-Karasinski (or Lognormal) term
structure model is used.
aaCaplet_HW(r_option_type, princ, d_v, d_exp, d_e, d_t,
rate_ex, acc, a, vlt_rate, df_crv, intrp, stat)
Calculates fair value of a caplet or floorlet. The
aaRcap_HW(d_v, rcap2_obj, acc, df_crv, intrp, a, vlt_rate)
Calculates the fair value and the implied forward rate for
a table of caplets or floorlets. The
aaCaplet_MF(r_option_type, princ, d_v, d_exp, d_e, d_t,
rate_ex, acc, model_type, model_parms, df_crv, intrp, stat)
Calculates fair value of a caplet or floorlet using a
multi-factor term structure model.
aaRcap_MF(d_v, rcap2_obj, acc, df_crv, intrp,
model_type, model_parms)
Calculates the fair value and the implied forward rate for
a table of caplets or floorlets using a multi-factor term structure model.
aaCaplet_LMM(r_option_type, princ, d_v, d_exp, d_e, d_t,
rate_ex, acc, model_vol, model_parms, scalfac_tbl, df_crv, intrp, stat)
Calculates fair value of a caplet or floorlet using the
Libor Market Model.
aaCapletVltGen_LMM(d_v, d_e, acc, vol_tbl, scale_fact)
Generates the Black volatility for a caplet for a
functional form of the instantaneous volatilities for the Libor Market Model.
aaRCapAsian(d_v, r_option_type, avg_type, rcap_obj,
reset_tbl, acc, df_crv_acc, df_crv_disc, scale_rate, intrp)
Calculates fair value and risk statistics for a series of
caplets where the rate is based on an average or a weighted average of the
reset rates.
Description of Inputs
|
Input Argument |
Type |
Description |
|
d_v |
Date |
Value date |
|
d_exp |
Date |
Option expiry date |
|
d_e |
Date |
Effective date of cap(let)/floor(let) |
|
d_t |
Date |
Terminating date of caplet/floorlet |
|
d_m |
Date |
Maturity date of cap/floor |
|
d_f_cpn |
Date |
Odd first caplet/floorlet terminating date in a cap/floor |
|
d_l_cpn |
Date |
Odd last caplet/floorlet terminating date prior to
maturity date of a cap/floor |
|
d_cm_reset |
Date |
Reset date for constant maturity yield |
|
d_cm_e |
Date |
Effective date for constant maturity yield |
|
paydate |
Date |
Caplet/floorlet payment date |
|
freq |
Number |
Frequency of the cap |
|
freq_cm |
Number |
Frequency of the underlying constant maturity yield |
|
eff_mktdays |
Number |
Number of business days prior to the effective date that
the rate is fixed |
|
npa, princ |
Number |
Notional principal amount |
|
payout |
Number |
Cash payoff for a digital option. Note that payout is treated like a notional
principal amount in the sense that the cash payoff is payout × accrual
factor, where accrual factor is the year fraction of the caplet/floorlet
calculated according to acc_pay. |
|
caplet_tbl,
rcap_obj, rcap2_obj |
Table |
Table of caplet information |
|
CM_caplet_tbl |
Table |
Table of caplet and constant maturity yield information |
|
price |
Number |
Option price |
|
r_option_type |
Number |
Option type (cap(let) or floor(let)) |
|
avg_type |
Number |
Type of averaging for Asian options |
|
capsettle |
Number |
Caplet/floorlet settlement (paid in advance or in-arrears) |
|
set_pay |
Number |
Rate setting (set in advance or in-arrears) |
|
rate_reset |
Rate |
Known reset rate |
|
cm_reset |
Rate |
Known reset rate for constant maturity yield |
|
r_table, reset_tbl, r_rate_obj |
Table |
Table of known rates |
|
scale_rate, scalefactor |
Number |
Rate scale factor |
|
rate_ex |
Rate |
Exercise (strike) rate |
|
acc_rt |
Number |
Accrual method for rate terms |
|
acc_cm |
Number |
Accrual method for underlying constant maturity yield |
|
acc_pay |
Number |
Accrual method for payment periods |
|
hl |
Table |
|
|
d_rul |
Number |
Business day convention |
|
d_rul_cm |
Number |
Business day convention for the underlying constant
maturity yield |
|
d_rul_pay |
Number |
Business day convention for payment dates |
|
vlt, vlt_fwd |
Rate |
Volatility of forward rate |
|
vlt_crv |
Table |
Table of forward rate volatilities |
|
vlt_cm |
Rate |
Volatility of constant maturity yield |
|
vol_corr_tbl |
Table |
Volatility and correlation table for swap and forward
rates |
|
corr_cm |
Rate |
Correlation between constant maturity yield and forward
rate |
|
numcf_cm_yld |
Number |
Number of cash flows in underlying constant maturity yield |
|
a |
Rate |
Short rate mean reversion (one-factor short rate model
parameter) |
|
vlt_rate |
Rate |
Short rate volatility (one-factor short rate model
parameter) |
|
model_type |
Number |
Type of two-factor short rate model |
|
model_vol |
Number |
Volatility parameterization for the Libor Market Model |
|
model_parms |
Table |
Model parameters (two-factor short rate, or Libor Market
Model) |
|
vol_tbl |
Table |
Table of forward rate volatilities (Black Model) |
|
scalfac_tbl |
Table |
Table of scaling factors for forward rate volatilities
(Libor Market Model) |
|
scale_fact |
Number |
Scale factor for forward rate volatilities (Libor Market
Model) |
|
df_crv_acc |
Table |
Discount factor curve for accruing rates |
|
df_crv_disc |
Table |
Discount factor curve for discounting rates |
|
method |
Number |
Convexity adjustment method |
|
intrp |
Number |
Interpolation method |
|
iter_year |
Number |
Number of tree time steps per year |
|
stat |
Number |
Output statistic |
Description of Outputs
|
Output Statistics |
Type |
Description |
|
Fair value |
Number |
Fair value of option ($) |
|
Dollar delta |
Number |
Change in fair value per 1 bp change in implied forward
rate ($/bp) |
|
Dollar gamma |
Number |
Change in delta per 1 bp change in implied forward rate
($/bp2) |
|
Dollar theta |
Number |
Change in fair value per 1 day change in value date
($/day) |
|
Dollar vega |
Number |
Change in fair value per 1% change in forward rate
volatility ($/1%) |
|
Implied forward rate |
Rate |
Forward rate implied from volatility |
|
Intrinsic value |
Number |
Fair value of option ($) |
Example
Let’s take a closer look at a rate cap by way of
example. Our subject is a commercial
real estate company that finances its current construction projects utilizing
bank operating lines. Upon completion of
the projects, the short term financing is replaced with a bond issue tied to
the property. Short term financing is
primarily by way of 3 month Libor. The
current term structure is increasing and the treasurer is concerned about the
possibility of a further spike in short term rates. In order to mitigate interest exposure, the
treasurer decides to enter into a one year rate cap.
The cash flow on each payment date can be separated into
two components as shown in the diagram below.
First, interest expense is paid on the original loan at the prevailing 3
month Libor rate () . Second, if
the current Libor reset is greater than the cap rate , the borrower is compensated the difference between
the two rates. The net impact of the
second component is that interest expense is always calculated using a rate
which is less than or equal to the cap rate. The same is true for the remaining
cash flows, or caplets during the term of the cap. In the diagram we have separated the cap from
the underlying loan. However, in most
instances the loan and cap are provided by the same financial institution, in
which case there is usually just one net cash flow.
The payoff for each cash flow can be written as 
where
is the principal
amount,
is the
period for which the rate applies (e.g., 3 months),
is the current 3 month Libor rate as at the
last reset date, and
is the cap rate.
The payoff due to the cap is then 
.
When period does not start today but rather some time in
the future, is the forward rate
and 
can be thought of as
the expected payoff for an option on the forward rate with strike . Since each cash flow
is only dependent on the Libor rate which applies to a particular period , a cap can be thought of as a strip of options
each written on a forward rate of term . Given that you cannot exercise the
options early, each caplet can be thought of as a European option on a forward
rate, in which case we can use the Black option model for valuation. The value of the cap is then just the sum of
the values of the individual caplets.
Today is June 12, 1996.
Bank B has priced a spot one year cap with a strike of 6% at 31.5 basis
points of the notional amount.
Alternatively, for the same deal Bank C has provided an indicative
volatility of 16% on the quote services as opposed to a direct price. Our example is a one year cap on 3 month
Libor which can be broken down into four periods. The first period contains no option as the
rate has already been set. The second
period is a one period option on a one period rate. The third period is a two period option on a
one period rate, etc. This is shown in
the following diagram.
|
|
period 1 |
period 2 |
period 3 |
period 4 |
|
option 1 |
<=======> |
|
|
|
|
option 2 |
|
<======= |
|
|
|
option 3 |
|
|
<======> |
|
|
option 4 |
|
|
|
<======> |
Our treasurer knows that he can construct his own
rate cap using options on Eurodollar futures and decides to compare that price
to the one quoted by Bank B. In order to
do this, the treasurer looks at the option contracts expiring on 19-Jun-1996,
19-Sep-1996, 18-Dec-1996, and 21-Mar-1997.
Since there is a theoretical 90 day Libor deposit underlying each of
these contracts, the cap runs from19-Jun-1996 to 18-Jun-1997.
Note: The Eurodollar futures dates do not
exactly match those offered by Bank B, but are close enough to provide a good
comparison. We have also assumed that
option contracts expire on the effective date of the underlying deposit,
whereas they actually expiry two business days prior to that date.
The mid prices for these option contracts were quoted at
0, 12, 51, and 63 basis points or a total price of 126 basis points. Since each basis point is worth $25 ($1
million NPA x .25 years x 1 bp), the cost of the cap in dollars is $3,150 the
same as quoted by Bank B.
Note: The price as quoted in basis points by the
dealer is not the same as the basis points obtained from the options on
Eurodollar futures. This is because the
underlying Libor deposit for each Eurodollar option is .25 years. The price in dollars is then 126 bps x $1
million x .25 = $3,150, which is equivalent to the dealer price (31.5 bps x $1
million = $3,150).
The table below incorporates market data into the Black
option model in order to determine price.
For example, the column titled “period 1” contains all of the
information required to value the first caplet.
The fair value of the caplet is shown across from the headings “Results
1”. The fair value of the cap is then
the sum of the fair values of the individual caplets. This is shown under the “Total” column in
basis points and in dollars.
|
Input Description |
period 1 |
period 2 |
period 3 |
period 4 |
Total |
|
Option Expiry |
19-Jun-1996 |
18-Sep-1996 |
18-Dec-1996 |
21-Mar-1997 |
|
|
Option Period |
7 |
98 |
189 |
282 |
|
|
Libor Period (e --> t) |
90 |
90 |
90 |
90 |
|
|
Eurodollar Futures Price |
94.42 |
94.09 |
93.68 |
93.49 |
|
|
Forward Rate |
5.58% |
5.91% |
6.32% |
6.51% |
|
|
Cap Rate (strike rate) |
6.00% |
6.00% |
6.00% |
6.00% |
|
|
Notional Amount |
$ 1,000,000 |
$ 1,000,000 |
$ 1,000,000 |
$ 1,000,000 |
|
|
Risk Free Rate |
5.4243% |
5.574% |
5.778% |
6.015% |
|
|
DFe |
0.998946386 |
0.98505254 |
0.97055908 |
0.95500543 |
|
|
DFt |
0.985202807 |
0.97071029 |
0.95546277 |
0.93971162 |
|
|
Volatility |
11.9% |
13.2% |
20.0% |
16.4% |
|
|
Results 1 |
|
|
|
|
|
|
price in bps |
0.00 |
11.83 |
51.19 |
62.98 |
125.99 |
|
price in $ |
0.00 |
295.63 |
1,279.78 |
1,574.38 |
3,149.79 |
|
Results 2 |
|
|
|
|
|
|
quoted volatility (mid) |
0.16 |
0.16 |
0.16 |
0.16 |
|
|
price in bps |
0.00 |
15.51 |
46.46 |
64.36 |
126.33 |
|
price in $ |
0.05 |
387.87 |
1,161.50 |
1,608.94 |
3,158.36 |
|
Output |
Output Description |
|
Option Expiry |
Option expiration date for each caplet |
|
Option Period |
Number of days from value date to the option expiration
date |
|
Libor Period (e --> t) |
term of the underlying Libor deposit (90 days) |
|
Eurodollar Futures Price |
Futures price (ex. 95.10) |
|
Forward Rate |
Implied forward rate given the futures price (ex. 4.90%) |
|
Cap Rate (strike rate) |
Contractual cap (strike) rate |
|
Notional Amount |
Notional (principal) amount of the contract |
|
Risk Free Rate |
Deposit rate from value date until the expiration date of
the option |
|
DFe |
Discount factor on the expiration date of the option
calculated using Risk Free Rate |
|
DFt |
Discount factor on the maturity date of the underlying
Libor deposit |
|
Volatility |
Volatility of the forward rate |
The totals under “Results 1” use the implied
volatilities obtained from the options on Eurodollar futures contracts. Since we are using market implieds, we expect
our fair value to equal the quoted price which is indeed the case. The more interesting question is to use the
volatility quoted by Bank C to determine if we obtain the same result. Using an implied of 16% we indeed price the
cap at 126 bps. This is shown in the
“Results 2” section. Given the above analysis, the treasurer can be confident
that he or she is obtaining a fair price.
References
[1]
[2]
Tompkins, Robert, (1992), ’The A to Z of Caps, From
Black-Scholes to Black Holes’, Risk Magazine Ltd.,
Disclaimer
With respect to this document,
FinancialCAD Corporation (“FINCAD”) makes no warranty either express or
implied, including, but not limited to, any implied warranty of merchantability
or fitness for a particular purpose. In no event shall FINCAD be liable to
anyone for special, collateral, incidental, or consequential damages in
connection with or arising out of the use of this document or the information
contained in it. This document should not be relied on as a substitute for your
own independent research or the advice of your professional financial,
accounting or other advisors.
This information is subject to change
without notice. FINCAD assumes no responsibility for any errors in this document
or their consequences and reserves the right to make changes to this document
without notice.
Copyright
Copyright ©
FinancialCAD Corporation 2008. All rights reserved.