Black-Scholes Generalized

Overview

The seminal work of Fischer Black and Myron Scholes in 1973 produced an elegant closed form solution for pricing European style call options on stock. Assumptions under which the formula was derived include:

· the option can only be exercised on the expiry date (European style);

· the underlying instrument pays a constant dividend yield;

· there are no taxes, margins or transaction costs;

· the risk free interest rate is constant;

· the price volatility of the underlying instrument is constant; and

· the price movements of the underlying instrument follow a lognormal distribution.

Formulas & Technical Details

A Brief Overview of the Analytics

Formulas

where

and

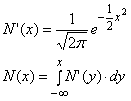
where

= theoretical value of an option

= price of the underlying

= exercise price

= time to expiration in years (act/365)

= annual volatility in percent

= risk free interest rate (converted to act/365)

= continuous dividend yield (converted to act/365)

= base of the natural logarithm

= natural logarithm

= cumulative normal distribution function

= normal density function

= positive one for call options and negative one for put options

Delta

Gamma

Theta

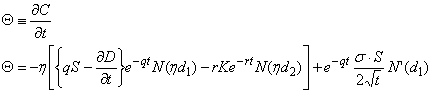
Vega

Rho1 ( risk free rate or domestic rate)

Rho2 (dividend rate , foreign rate or repo spread)

For details about the calculation of Greeks, see the Greeks of Options on non-Interest Rate Instruments FINCAD Math Reference document.

Important

FINCAD uses annually compounded rates. Let and be annually compounded rates. In each of the formulas above, one should replace by ln(1+) and by ln(1+). Also, the statistics and are returned as the derivative with respect to and (rather than and ). As a consequence:

= ( above) / (1+) and

= ( above) / (1+).

The time to expiry in years is calculated using the actual/365 daycount convention. Internally, and are first converted from their defined daycount conventions to act/365 rates. In this way, the discount factors and take into account the given daycount conventions (or accrual methods) of the rates. The option time , which is multiplied by to calculate and , is always calculated using actual/365.

Also, is returned as a daily rate = ( above) / 365.

Discrete Dividends

If the dividends are in the form of discrete payments, as opposed to a continuous yield, the above must be set to zero and the price of the underlying must be modified to account for the present value of all the future dividend payments. However, if is reinterpreted as a repo rate , then the same formulae can be used with the modified price of the underlying:

where

and is the time until the dividend payment . Since is a function of both the risk free rate and the time until maturity , the greeks and will be affected by this substitution. The modified equations are given below:

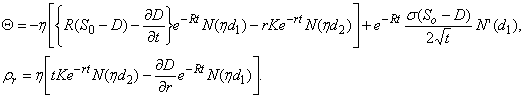
Repo Spread and Continuous Dividend Yield

The repo agreement is a contract whereupon two parties exchange collateral (in this case the underlying asset) for cash, with an agreement to perform the reverse exchange at a predetermined time in the future when the cash has accumulated interest at a predetermined rate: the “repo rate” [2]. The repo rate represents the rate of a “repurchase agreement” that is usually necessary when short selling the underlying asset. Therefore, the repo spread input need only be used when hedging the option requires a short position in the underlying (that is for long calls or short puts); otherwise, enter a zero repo spread. The repo spread is analogous to a continuous dividend yield, in that in the risk-neutral measure the underlying grows at the risk-free rate minus the repo spread (or continuous dividend yield).

The repo spread input to the function aaBSGdcf() can be entered as a single spread or a discount factor curve. If entering a single spread, this spread equals the risk-free rate of interest minus the repo rate quoted in the market when both rates are quoted as annual, act365(fixed) (conversion to this rate basis and accrual factor can be done with the FINCAD function aaConvert_cmpd2()). A positive repo spread describes the case where the repo rate is greater than the risk-free rate. If you wish to enter the repo spread as a “discount factor” curve, create this curve by the following procedure: First construct the risk-free discount factor curve from money market rates (using, for example, one of FINCAD’s curve bootstrapping functions such as aaSwapCrv()) and the repo rate “discount factor” curve in a similar way from quoted repo rates of different tenors. If the dates in these two discount factor curves do not match, find the missing discount factors by interpolation, using aaInterp(). The repo spread “discount factor” curve can then be created by taking the ratio of the risk-free to the repo rate discount factors on each date (more explicitly the risk-free discount factor divided by the repo rate discount factor, this ratio will be greater than one if the repo rate is greater than the risk-free rate).

This input also provides the ability to enter a term structure of dividend yields. For example, the case where discrete dividends are known up to a particular date and assumed continuous after this date can be handled by using a combination of discrete dividends and the discount factor input. Simply set the continuous dividend yield discount factor equal to one on all dates prior to the last known dividend date to achieve the desired result.

FINCAD Functions

Pricing and Risk Statistics

aaBSG()

Calculates the fair value and risk statistics for a European option on securities that pay a continuous dividend yield using the Black Scholes Generalized model.

aaBSdcf()

Calculates the fair value and risk statistics for a European option on securities with discrete cash flows using the Black-Scholes model. The risk free rate can be entered as a single rate, as a rate curve or as a discount factor curve.

aaBSGdcf()

Calculates the fair value and risk statistics for a European option with both a repo rate discrete dividends.

Implied Volatility

aaBSG_iv()

Calculates the implied volatility for a European option on securities that pay a continuous dividend yield using the Black Scholes Generalized model.

aaBSdcf_iv()

Calculates the implied volatility for a European option on securities with discrete cash flows using the Black-Scholes model. The risk free rate can be entered as a single rate, as a rate curve or as a discount factor curve.

aaBSG_delta_smile_iv()

Calculates the implied volatility for a European option (using the Black-Scholes Generalized model) given an exercise price and a volatility smile (volatility at various deltas).

Implied Strike Price

aaBSG_ik()

Calculates the implied strike price given the volatility and price for a European call or put option using the Black Scholes Generalized model.

aaBSdcf_ik()

Calculates the implied strike price given the volatility and price for a European call or put option on equities with discrete dividend payments. The risk free rate can be entered as a single rate, as a rate curve or as a discount factor curve.

Implied Underlying Spot Price

aaBSG_iu()

Calculates the implied underlying price given the volatility and price for a European call or put option using the Black Scholes Generalized model.

aaBSdcf_iu()

Calculates the implied underlying price given the volatility and price for a European call or put option on equities with discrete dividend payments. The risk free rate can be entered as a single rate, as a rate curve or as a discount factor curve.

Simulation

aaBSG_sim()

Calculates the fair value and risk statistics for European options on securities with continuous dividend yields using the Black Scholes Generalized model.

aaBSdcf_sim()

Calculates the fair value and risk statistics for European options on securities with discrete cash flows using the Black-Scholes model. The risk free rate can be entered as a single rate, as a rate curve or as a discount factor curve.

Example

Today is February 1, 1995. You are considering a covered write on a stock that closed last night at $87.50. You plan to sell 45 day $90.00 calls on a stock that yields 3.5% and expires on March 18, 1995. The 45 day Eurodeposit rate can be interpolated to be 5.93% (accrual method is actual/360). Using an estimated volatility of 26%, what is the delta for this option?

aaBSG

Argument	Description	Example Data	Switch
price_u	price of underlying interest	87.5
ex	exercise price	90
d_exp	expiry date	18-Mar-1995
d_v	settlement date	01-Feb-1995
vlt	annual volatility estimate	0.26
rate_ann	riskless deposit rate (annual compounding)	0.0593
cost_hldg	annual holding cost input as a rate	0.035
option_type	option type	1	call
stat	statistics to be returned	2	delta
acc_rate	method of interest accrual for rate	2	actual/ 360
acc_cost_hldg	method of interest accrual for holding cost	1	actual/ 365 (fixed)

Result

Statistic	Description	Value
1	delta	0.4071163

Therefore a $1.00 change in the underlying price should result in a $.41 change in the option value.

Related Functions

We note that there is a suite of aaBS*() functions (not aaBSG()). These are simply versions of aaBSG*() that do not allow the input of a dividend rate (or holding cost, …).

· American Style Options: there are many functions available.

· Bermudan Style Options: there are many functions available.

· Quanto: aaQuanto_opt() and others.

· FX Specific (Garman-Kohlhagen): there are several functions available.

· There are many versions of calls and puts with barriers, average-based, on spreads, baskets. We recommend searching under the specific option type.

References

[1] Bookstaber, Richard, (1991), Option Pricing and Investment Strategies 3rd Edition, Probus Publishing Company.

[2] Choudry, Moorad, (2006), An Introduction to the Repo Market 3rd Edition, John Wiley & Sons Ltd.

[3] Cox, John; Rubinstein, Mark, (1985), Options Markets, Prentice Hall.

[4] ‘From Black Scholes to Black Holes’, (1994), Risk.

[5] Natenburg, Sheldon, (1988), Option Volatility and Pricing Strategies, Probus Publishing Company.

Disclaimer

With respect to this document, FinancialCAD Corporation (“FINCAD”) makes no warranty either express or implied, including, but not limited to, any implied warranty of merchantability or fitness for a particular purpose. In no event shall FINCAD be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of the use of this document or the information contained in it. This document should not be relied on as a substitute for your own independent research or the advice of your professional financial, accounting or other advisors.

This information is subject to change without notice. FINCAD assumes no responsibility for any errors in this document or their consequences and reserves the right to make changes to this document without notice.